Плотность распределения (дифференциальная функция распределения)

Стр 1 из 3Следующая ⇒

Случайные события. Основные формулы онлайн

Основные формулы комбинаторики

Число перестановок

Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅nPn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n

Число размещений

Anm=n⋅(n−1)⋅...⋅(n−m+1)Amn=n⋅(n−1)⋅...⋅(n−m+1)

Число сочетаний

Cmn=AmnPm=n!m!⋅(n−m)!Cnm=AnmPm=n!m!⋅(n−m)!

Классическое определение вероятности

P(A)=mn,P(A)=mn,

где mm - число благоприятствующих событию AA исходов, nn - число всех элементарных равновозможных исходов.

Вероятность суммы событий

Теорема сложения вероятностей несовместных событий:

P(A+B)=P(A)+P(B)P(A+B)=P(A)+P(B)

Теорема сложения вероятностей совместных событий:

P(A+B)=P(A)+P(B)−P(AB)P(A+B)=P(A)+P(B)−P(AB)

Вероятность произведения событий

Теорема умножения вероятностей независимых событий:

P(A⋅B)=P(A)⋅P(B)P(A⋅B)=P(A)⋅P(B)

Теорема умножения вероятностей зависимых событий:

P(A⋅B)=P(A)⋅P(B|A),P(A⋅B)=P(B)⋅P(A|B).P(A⋅B)=P(A)⋅P(B|A),P(A⋅B)=P(B)⋅P(A|B).

P(A|B)P(A|B) - условная вероятность события AA при условии, что произошло событие BB,

P(B|A)P(B|A) - условная вероятность события BB при условии, что произошло событие AA.

P(A|B)=P(AB)P(B),P(B|A)=P(AB)P(A).

Формула полной вероятности

P(A)=∑k=1nP(Hk)⋅P(A|Hk),P(A)=∑k=1nP(Hk)⋅P(A|Hk),

где H1,H2,...,HnH1,H2,...,Hn - полная группа гипотез.

Формула Байеса (Бейеса). Вычисление апостериорных вероятностей гипотез

где H1,H2,...,HnH1,H2,...,Hn - полная группа гипотез.

Формула Бернулли

Pn(k)=Ckn⋅pk⋅(1−p)n−k=n!k!⋅(n−k)!⋅pk⋅(1−p)n−kPn(k)=Cnk⋅pk⋅(1−p)n−k=n!k!⋅(n−k)!⋅pk⋅(1−p)n−k

вероятность появления события ровно kk раз в nn независимых испытаниях, pp - вероятность появления события при одном испытании.

Наивероятнейшее число наступления события

Наивероятнейшее число k0k0 появления события при nn независимых испытаниях (где pp- вероятность появления события при одном испытании):

np−(1−p)≤k0≤np+p.np−(1−p)≤k0≤np+p.

Локальная формула Лапласа

Pn(k)=1npq−−−√φ(k−npnpq−−−√)Pn(k)=1npqφ(k−npnpq)

вероятность появления события ровно kk раз при nn независимых испытаниях, pp - вероятность появления события при одном испытании, q=1−pq=1−p.

Интегральная формула Лапласа

Pn(m1,m2)=Φ(m2−npnpq−−−√)−Φ(m1−npnpq−−−√)Pn(m1,m2)=Φ(m2−npnpq)−Φ(m1−npnpq)

вероятность появления события не менее m1m1 и не более m2m2 раз при nn независимых испытаниях, pp - вероятность появления события при одном испытании, q=1−pq=1−p.

11. Оценка отклонения относительной частоты от постоянной вероятности pp

P(∣∣mn−p∣∣≤ε)=2Φ(ε⋅np(1−p)−−−−−−−√)P(|mn−p|≤ε)=2Φ(ε⋅np(1−p))

εε - величина отклонения, pp - вероятность появления события.

II. Случайные величины. Основные формулы онлайн

Ряд распределения дискретной случайной величины

			…….
			…….

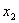
Сумма вероятностей всегда равна 1.

Функция распределения (интегральная функция распределения)

Функция распределения случайной величины определяется по формуле . Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения , то функция распределения выражается как .

Плотность распределения (дифференциальная функция распределения)

Плотность распределения случайной величины определяется по формуле. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки: 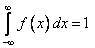(площадь под кривой равна 1).

Дата добавления: 2019-03-09; просмотров: 118; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!