Расчет по методу предельной несущей способности

В методе расчетных сопротивлений, рассмотренном ранее, условие прочности ограничивает достижение хотя бы в одной точке поперечного сечения напряжения, равного расчетному сопротивлению для данного материала, т.е. R.

В методе предельной несущей способности условие прочности относится не к напряжению, а к допускаемому изгибающему моменту, который определяется как отношение предельного изгибающего момента к коэффициенту запаса n.

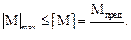                          (7.12)

При одинаковом значении коэффициента запаса по напряжениям и по нагрузкам (т.е. n = ) метод предельной несущей способности дает некоторую экономию материала.

Рассмотрим метод предельного равновесия при изгибе балок из упруго-пластического материала (например, сталь).

Для упрощения задачи примем в качестве расчетной диаграмму Прандтля (рис. 7.5). При s < s_S материал работает линейно-упруго, поэтому для вычисления нормальных напряжений в поперечном сечении балки справедлива формула:

При достижении максимального значения нормального напряжения  в наиболее удаленной от центральной (нейтральной) оси сечения точке предела текучести ( = s_S) продольные волокна в этой точке неограниченно деформируются при постоянном напряжении  s = s_S.

При таком предположении рассмотрим стадии, проходящие балкой при увеличении изгибающего момента в данном сечении вплоть до исчерпания несущей способности (рис. 7.6).

При постепенном возрастании максимального изгибающего момента линейно-упругая стадия работы балки заканчивается при достижении текучести в самой напряженной крайней точке (рис. 7.6б). Соответствующий данному состоянию изгибающий момент определится из условия

 

Отсюда                  М_Т = .                                 (7.13)

При дальнейшем увеличении внешней силы, а значит и максимального изгибающего момента, наступает упруго-пластичес­кая стадия работы балки. Зона текучести при этом будет расширяться от крайних точек, а эпюра  при М_Т М М_пред будет иметь вид (рис. 7.6в). В пределе эпюра  превратится в ступенчатую эпюру с ординатами s = ±s_S. В данный момент это сечение будет работать в чисто пластической стадии (рис. 7.6г).

 

Если центральная ось Z является осью симметрии сечения, то обе крайние точки достигают текучести одновременно.

Состояние сечения, когда во всех точках развиваются пластические деформации, называют пластическим шарниром.

При этом балка, если она была статически определимой, как бы превращается в механизм, продолжающий увеличивать прогибы при постоянной внешней нагрузке, равной предельной. Такое состояние называют пластическим механизмом. В поперечном сечении, где образовался пластический шарнир, внутренний момент обозначим М_пред и назовем его пластическим предельным моментом.

Таким образом, наиболее напряженное сечение балки проходит три стадии работы:

– линейно упругую ( );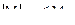

– упруго пластическую (М_Т < < М_пред.);

– чисто пластическую (пластический шарнир) (|M|_max = M_пред).

Получим формулу для определения М_пред на примере сечения с одной осью симметрии (рис. 7.6).

В упругой стадии эпюра  линейна и нулевая (нейтральная) линия совпадает с центральной осью Z.

В общем случае при образовании пластического шарнира нейтральная ось (н.о) n–n смещается от центра тяжести сечения (точки С). В этот момент все сечение делится на две части: часть, растягиваемую постоянным напряжением s_S с площадью А_р и соответствующей силой N_P = А_P × s_S и часть сжимаемую постоянным напряжением s_S с площадью А_сж с действующей силой N_cж = –А_сж×s_S. Так как суммарная продольная сила в сечении при поперечном изгибе равна нулю, то из условия:

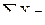N_Р + N_сж = А_Р –А_сж = 0

получим                А_р = А_cж =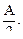

Таким образом, при образовании пластического шарнира нейтральная ось делит площадь поперечного сечения на две равновеликие части. Эта ось на рис. 7.4 показана пунктиром.

Внутренний момент М_пред найдем как момент всех элементарных сил (s_S × dA) относительно нейтральной оси n–n, (рис. 7.6а).  

    (7.14)

Здесь – S статический момент растянутой зоны относительно нейтральной оси в предельном состоянии n–n; S 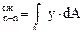 – то же для сжатой зоны.

Обозначим            S + S 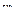= W_пл,                        (7.15)

где W_пл – пластический момент сопротивления сечения в отличие от W_Z =  осевого момента сопротивления в упругой стадии.

Формулу (7.14) можно записать в виде, аналогичном соответствующей формуле в упругой стадии:

М_пред = 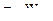                      (7.16)

Примеры расчета

ПРИМЕР 7.1

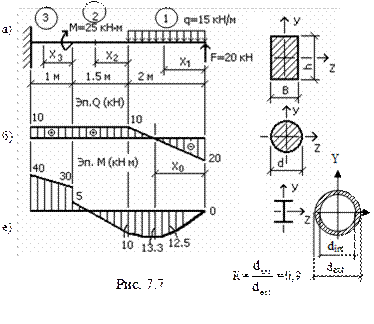
Для балки, изображенной на рис. 7.7а, требуется:

– построить эпюры М и Q;

– подобрать сечение в четырех вариантах (рис. 7.7б, в, г, д) и проверить прочность подобранных сечений по нормальным и касательным напряжениям.

 

 

РЕШЕНИЕ

А. Построение эпюр М и Q

1. В пределах грузовых участков 1, 2, 3 (рис. 7.7а) проводим сечения на расстоянии x_i от начала каждого участка. При этом рассматриваем правую, свободную от опоры, часть балки, а левую отбрасываем.

Заменяя действие отброшенной части неизвестными

положительными поперечной силой Q_i(x_i) и изгибающим моментом М_i(x_i) и рассматривая равновесие выделенной части балки, находим выражения внутренних усилий на участках.

При построении эпюр М и Q и их проверке используем дифференциальные зависимости Д.И. Журавского между М, Q и q:

 (7.17)

В зависимостях (7.11) перед q ставится знак "минус", если распределенная нагрузка направлена вниз.

1-й грузовой участок (рис. 7.8)        

Составим уравнения равновесия для 1-го участка.

= 0; Q₁(x₁) – qx₁ + F = 0; Так как Q₁(x₁) – линейная функция, то для построения эпюры Q на этом участке достаточно рассмотреть два сечения:

х₁ = 0 м,     Q₁(0) = – 20 кН;

х₁ = 2,0 м,  Q₁(2) = 10 кН.

Строим эпюру Q из которой видно (см. рис. 7.7е), что на первом участке эпюра поперечных сил имеет нулевую ординату. В соответствии с дифференциальной зависимостью (7.17) между М и Q ( ) эпюра изгибающих моментов на этом участке будет иметь экстремум.

Приравнивая Q₁(х₁) к нулю при х₁ = х₀, получим:

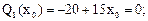
 –М₁(х₁) – q + F×x₁ = 0;

Функция М₁(х₁) – квадратичная, поэтому для построения графика этой функции на данном участке (эпюры М), находим не менее трех значений изгибающего момента:

х₁ = 0 м,        М₁(0) = 0 кН×м;

х₁ = х₁ = 1,33 м, М₁(х₀) = M_extr = 13,3 кН×м;

х₁ = 2,0 м,        М₁(2) = 10 кН×м.

По найденным значениям строим эпюру М на первом участке под эпюрой поперечных сил. Изгибающие моменты откладываем со стороны растянутых волокон, т.е. "плюс" – вниз (растягиваются нижние волокна), "минус" – вверх (растягиваются верхние волокна) см. (рис. 7.7е, ж).

Аналогично построим эпюры на 2-м и 3-м грузовых участках:

2-й участок (рис. 7.9):

 

= 0; Q₂(x) – q 2 + F = 0;

Эпюра Q постоянна по длине данного участка.

 – М₂ (х₂) – q 2 (х₂ + ) + F (x₂ + 2) = 0;

Изгибающий момент на данном участке изменяется по линейному закону:

х₂ = 0 м,       

х₂ = 1,5 м,        

 

3-й участок (рис. 7.10):       

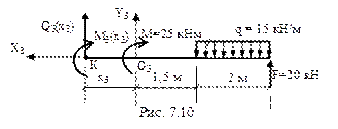
Рассматривая 3-й участок также вырежем правую часть балки. Начало локальной системы координат поместим в начале 3-го участка.

= 0; Q₃(x₃) – q 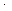2 + F = 0;

 

Эпюра Q постоянна по длине участка.

 –М₃(х₃) – М – q×2(х₃ + 1 + 1,5) + F × (x₃ + 3,5) = 0;

 (знак "минус" означает, что растягиваются верхние волокна);

х₃ = 1 м,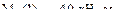

Эпюры М и Q, построенные по результатам расчётов, показаны на рис. 7.7е, ж.

Б. Подбор сечения

Из эпюр М и Q имеем: 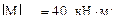= 20 кН.

1. Балка прямоугольного сечения (см. рис. 7.7б):

R = 10 МПа, R_s = 5 МПа, h = 4b.

Из условия прочности (7.2) определим требуемую величину осевого момента сопротивления при :

Осевой момент сопротивления для прямоугольного сечения при заданных соотношениях сторон определится по формуле:

Приравняем  и найдем размер сечения b:

Округляя в большую сторону, примем:

b = 11,5 см,    h = 4b = 4 11,5 = 46 см.

Проверим прочность подобранного сечения по нормальным и касательным напряжениям.

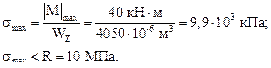
Прочность по нормальным напряжениям обеспечена. Недонапряжение в 1 % объясняется округлением размера сечения b в большую сторону.

Для проверки прочности по касательным напряжениям используем формулу (7.11):

20 кН, (из эпюры Q);

I

Наибольшие касательные напряжения для прямоугольного сечения возникают в точках, лежащих на центральной оси Z, так как S  для полусечения (отсечение проводится через точку К,находящуюся на центральной оси Z) имеет максимальное значение (рис. 7.11в):

S 11,5

b = b = 11,5 см. А^отс = b ; y = .

 

Прочность по касательным напряжениям обеспечена с большим запасом.

2. Балка сплошного круглого сечения, материал – дерево,

Требуемый осевой момент сопротивления берем из предыдущего расчета, так как он не зависит от формы сечения

Осевой момент сопротивления для круглого сечения:

      где

Из условия  имеем:

 отсюда –

Округляя, примем d = 0,35 м.

Проверим прочность подобранного сечения по нормальным напряжениям:

Прочность балки по нормальным напряжениям обеспечена. Небольшое недонапряжение (–5 %) объясняется округлением диаметра в большую сторону.

Наибольшая ширина данного сечения d находится на центральной оси, значит максимальные касательные напряжения будут небольшими, поэтому для данного сечения проверку по касательным напряжениям можно не производить.

3. Балка из прокатного двутавра (см. рис. 7.7г).

Из условия прочности по нормальным напряжениям определяем требуемое значение осевого момента сопротивления:

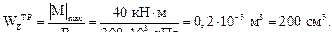
Из таблицы сортаментов по ГОСТ 8239-89 для стального проката находим двутавр, имеющий близкий к требуемому осевой момент сопротивления:

Двутавр № 20,

Проверим прочность этого двутавра:

Определим процент перенапряжения.

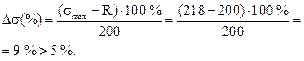
Такая величина перенапряжения считается недопустимой, поэтому проверим прочность двутавра № 22.

Для этого двутавра из сортамента имеем  

Имеет место недонапряжение

Окончательно выбираем двутавр № 22.

Проверим прочность подобранного сечения по касательным напряжениям.

Наибольшие касательные напряжения будут в точках сечения, лежащих на центральной оси, так как статический момент полусечения имеет максимальное значение, а толщина в этом месте – минимальная.

Для двутавра № 22 из таблицы сортаментов для прокатных двутавров (ГОСТ 8239-89) получаем:

I ;

b_К = s_c = 5,4 мм = 0,54 см;

S  – статический момент полусечения.

Тогда

Прочность балки по касательным напряжениям обеспечена с большим запасом.

 

4. Балка из стальной трубы (см. рис. 7.7д)

R = 200 МПа; R_S = 100 МПа;

Из предыдущего, третьего пункта, имеем:

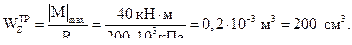
Для кольцевого поперечного сечения:

Из условия: W_Z = W  определяем наружный диаметр d_ext:

200 см³ =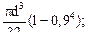

d_ext =

Округляя, примем d_ext = 18 см; d_int = 0,9d_ext = 0,9 18 = = 16,2 см.

Проверим подобранное сечение по нормальным и касательным напряжениям:

Относительная величина перенапряжения составляет:

= 1,6 % < 5 %, что допустимо и объясняется округлением требуемого диаметра в меньшую сторону.

Проверяем прочность поперечного сечения по касательным напряжениям. Опасной является точка, лежащая на центральной оси Z, так как для этой точки статический момент полусечения достигает максимального значения, а ширина сечения имеет минимальную величину. Для проверки прочности используем формулу (7.11):

Ширина сечения на уровне центральной оси b_К определится как разность диаметров: b_К = d_ext – d_int = 18 – 16,2 = 1,8 см.

Статический момент отсеченной части сечения выше центральной оси Z определим как разность статических моментов большего и меньшего полукругов:

Максимальное касательное напряжение составляет:

Условие прочности по касательным напряжениям выполняется с большим запасом.

 

ПРИМЕР 7.2

Для балки, изображенной на рис. 7.12а, требуется:

– построить эпюры М и Q;

– подобрать размеры стальных составных сечений в двух вариантах (по рис. 7.12г, д).

 

 

РЕШЕНИЕ

А. Построение эпюр М и Q

Определяем реакции опор

       Н_А = 0;

   

V_B = 56,67 кН;

   

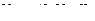
Проверка:

В отличие от предыдущего примера определим изгибающие моменты и поперечные силы в отдельных сечениях балки без составления функций для М и Q, используя только приведенные ранее (п. 7.1, стр. 122) рабочие правила и правила знаков.

Сечения проведем бесконечно близко в начале и в конце грузовых участков, на которых отсутствует распределенная нагрузка q. Дополнительное сечение проведем по середине участка, где имеется q (рис. 7.12 а).

Вычислим значения Q и М в этих сечениях. Для сечений 1–1, 2–2, 3–3 будем рассматривать левую отсеченную часть, а для остальных – правую часть.

 

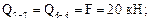
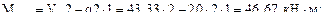
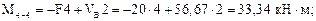
По полученным результатам строим эпюры М и Q (рис. 7.12б, в).

Эпюру М строим со стороны растянутых волокон, т.е. значения М со знаком "минус" откладываем вверх. Из эпюры Q видно, что экстремальное значение изгибающего момента на 1-м грузовом участке будет в сечении на расстоянии х₀, т.е. там, где Q(х₀) = 0. Из этого условия находим величину х₀:

Q(х₀) = V_A – qx₀ = 43,33 – 20x₀ = 0; x₀ =

Вычисляем в этом сечении величину М_экстр:

М_экстр. = М(х = х₀) = 43,33 2,17–20

При анализе правильности эпюр с учетом дифференциальных зависимостей между М, Q и q (7.13) замечаем:

– на эпюре М имеется скачок там, где приложен внешний сосредоточенный момент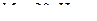

– на эпюре Q имеются скачки в сечениях, где приложены внешние сосредоточенные силы, в том числе и опорные реакции;

– на участках, где отсутствует q, эпюра моментов изменяется по линейному закону, а эпюра Q постоянна;

– на участке, где имеется равномерно распределенная нагрузка интенсивностью q, эпюра М меняется по закону квадратной параболы, выпуклостью в сторону действия q, а эпюра Q – по линейному закону. Тангенс угла наклона этой прямой к продольной оси балки равен интенсивности нагрузки q.

Б. Подбор сечения балки

1. Вариант сечения по рис. 7.12г

R = 200 10³ кПа;       R_S = 100 10³ кПа.

А. Из условия прочности по нормальным напряжениям определяем требуемую величину осевого момента сопротивления.

Из эпюры изгибающих моментов получаем  |M|_max = = 46,94 кН×м.

Допускаем, = R и из этого условия определяем требуемое значение осевого момента сопротивления:

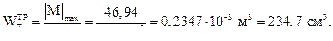
Определяем положение главной центральной оси Z и величину главного центрального момента инерции заданного сечения 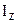 (см. главу 5). Геометрические характеристики плоских сечений:

Здесь у_с – расстояние от произвольно взятой оси Z' до центральной оси Z для всей фигуры; А_i – площади отдельных фигур:

А₁ = 10δ × 2s = 20s²;  А₂ = 22s×s = 22s²;  А₃ = 5s×2s = 10s²;

у_i – ординаты центров тяжестей отдельных фигур относительно произвольно взятой оси Z'. Пусть произвольная ось Z' совпадает с осью Z₃ (см. рис. 7.12г).

у₁ =  у₂ =

у₃ = 0, так как оси Z₃ и Z'  совпадают.

Отложим найденное расстояние y_Сот оси Z' и проведем общую центральную ось Z.

Осевой момент инерции всей фигуры относительно оси Z вычислим по формуле:

Здесь I_Zi – собственные моменты инерции простых фигур относительно их собственных центральных осей.

Так как все фигуры прямоугольники, то:

I_Z1 =

I_Z2 =

I_Z3 =

у_0i – расстояния от общей центральной оси Z до центральных осей простых фигур Z_i:

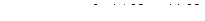
Б. Определим осевой момент сопротивления сечения.

Расстояния от центральной (нейтральной) оси Z до наиболее удаленных (крайних) точек сечения А и В (рис. 7.13а):

Отсюда:

Осевой момент сопротивления определим по формуле:

 

В. Приравняем найденное ранее значение требуемого осевого момента сопротивления к выражению для определения фактической величины осевого момента сопротивления и найдем параметр сечения d:

      

2. Расчет балки по 2-му варианту сечения (см. рис. 7.12д и 7.13а)         R = 200М Па, R_S = 100 МПа.

А. Определение осевого момента сопротивления сечения

Так как сечение имеет две оси симметрии, его центр тяжести находится на их пересечении.

Определим главный центральный момент инерции сечения относительно оси Z как разность моментов инерции двух прямоугольников, центры тяжести которых совпадают.

I_Z =

W_Z =  здесь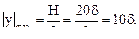

Б. Определение требуемого момента сопротивления сечения

Из условия прочности по нормальным напряжениям

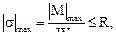 при = R получаем

W

В. Из условия W _Z = W  определим размер

393,6 = 234,7 см³;

Полученное значение  округляем по ГОСТ 103-76 для  стальной полосы и принимаем 9 мм = 0,9 см.

Г. Проверим прочность подобранного сечения по нормальным и касательным напряжениям

<R.

Имеется недонапряжение из-за округления размера сечения в большую сторону. Оценим его в процентах:

(%) =

Из рис. 7.13г видно, что наибольшие касательные напряжения будут в точке К, лежащей на центральной оси.

Условие прочности:      

    

 (из эпюры Q, см. рис. 7.12б);

I_Z = 3936 = 3936 0,9⁴ = 2582 см⁴;

в(у)_(к) = 2 = 2 0,9 = 1,8 см;

S 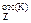 находим как разность статических моментов площадей, лежащих выше центральной оси Z, относительно этой же оси:

S

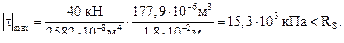
Условие прочности по касательным напряжениям выполняется с большим запасом.

 

ПРИМЕР 7.3

Для балки составного сечения (см. рис. 7.12г), рассчитанной в примере 7.2, требуется:

1. Выполнить полную проверку прочности балки при R = = 200 МПа, R_S = 100 МПа.

2. Подобрать размер сечения  по методу предельного равновесия (при коэффициенте запаса n = 1,2 и = 240 МПа) и сравнить его с величиной, полученной по методу расчетных сопротивлений в примере 7.2.

 

---

Дата добавления: 2019-02-26; просмотров: 642; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!