Моменты инерции простых сечений

⇐ ПредыдущаяСтр 13 из 22Следующая ⇒

Нижеприведенные формулы для определения моментов инерции простых сечений относительно их центральных осей получены из интегральных выражений для моментов инерции (5.4), (5.5), (5.6):

1. Прямоугольник

(5.10)

(5.11)

так как оси Z и Y – оси симметрии.

2. Круг

(5.12)

(5.13)

Здесь – полярный момент инерции сечения.

3. Полукруг

(5.14)

(5.15)

Рис. 5.5

4. Равнобедренный треугольник

(5.16)

(5.17)

5. Прямоугольный треугольник

(5.18)

(5.19)

(5.20)

Полезно запомнить, что в формулах (5.10), (5.11) и (5.16)–(5.19) возводится в куб размер стороны фигуры, перпендикулярной рассматриваемой оси.

В формуле (5.20) при определении центробежного момента инерции знак "минус" ставится тогда, когда острые углы треугольника находятся в отрицательных четвертях (т.е. 2-й и 4-й). В тех случаях, когда эти углы находятся в положительных четвертях (т.е. 1-й и 3-й), в формуле (5.20) ставится знак "плюс".

Главные центральные моменты инерции сложных симметричных сечений

Положение главных центральных осей и величины главных центральных моментов инерции для симметричных сечений определяются в следующем порядке:

1. Сложное сечение разбивается на простые фигуры (круг, прямоугольник, двутавр, уголок и т.п.) и проводятся их центральные оси Z_i и Y_i (как правило – горизонтально и вертикально).

2. Определяется по формулам (5.3) положение центра тяжести всего сечения и через эту точку проводятся его центральные оси Z и Y. При наличии двух осей симметрии центр тяжести всего сечения находится в точке их пересечения.

Если сечение обладает только одной осью симметрии, то по формулам (5.3) определяется только одна координата центра тяжести. Поясним это для фигуры, показанной на рис. 5.8:

а) оси Z' и Y' выбираем так, чтобы ось Y' совпала с осью симметрии фигуры, а ось Z' – чтобы было удобно определить расстояние до этой оси от центральных осей простых фигур;

б) определяем статический момент площади сечения относительно произвольной оси Z' по формуле:

= А₁у₁ + А₂у₂,

где А_i – площади сечений простых фигур; у_i – расстояния от произвольной оси Z' до центральных осей простых фигур Z_i. Расстояния у_i необходимо брать с учетом знаков;

в) определяем координату у_C центра тяжести по формуле (5.3):

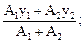
г) на расстоянии у_C от оси Z¢ проводим вторую центральную ось Z. Первой центральной осью является ось симметрии Y.

3. Моменты инерции относительно главных центральных осей Z и Y (рис. 5.8) определяем по формулам (5.9), которые в развернутом виде запишутся так:

так как одна из рассматриваемых осей

(ось Y) является осью симметрии.

В этих формулах:

– осевые моменты инерции простых фигур относительно своих центральных осей (собственные моменты инерции), которые определяются по формулам (5.10)–(5.19) или по таблицам сортаментов для прокатных элементов;

– расстояния от общих центральных осей сечения Z и Y до центральных осей простых фигур. В рассматриваемом примере и показаны на рис. 5.8;

A_i – площади простых фигур. Если простой фигурой является фигура, вырезанная от общей, т.е. "пустая" фигура, то в соответствующие формулы площади таких фигур A и их собственные моменты инерции подставляются со знаком "минус".

ПРИМЕР 5.1

Требуется определить главные центральные моменты инерции сечения, изображенного на рис. 5.9.

РЕШЕНИЕ:

1. Разбиваем сечение на простые фигуры и проводим их горизонтальные и вертикальные центральные оси Z_i и Y_i

2. Проводим центральные оси для всей фигуры, т.е. оси симметрии Z и Y.

3. Определяем расстояния от общих центральных осей Z и Y до центральных осей простых фигур и площади этих фигур:

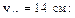
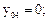
4. Вычисляем собственные центральные моменты фигур по формулам (5.10)–(5.17):

5. Определяем осевые моменты инерции всего сечения относительно центральных осей Z и Y:

Центробежный момент инерции так как Z и Y – оси симметрии. Поэтому вычисленные нами I_Z и I_Y поэтому являются главными центральными осями:

ПРИМЕР 5.2

Требуется определить главные центральные моменты инерции сечения показанного на (рис. 5.10).

РЕШЕНИЕ

1. Разбиваем сечение на простые фигуры и проводим их центральные оси и Y_i.

2. Проводим ось симметрии Y. Она является главной центральной осью заданного сечения.

3. Для определения положения 2-й главной центральной оси выбираем произвольную ось Z¢, перпендикулярную оси симметрии. Пусть эта ось совпадает с осью Z₃.

4. По формуле (5.3) определяем ординату у_с центра тяжести поперечного сечения по оси Y:

Откладываем размер у_C вверх от оси Z' и проводим 2-ю главную центральную ось Z.

5. Определяем осевые моменты инерции простых фигур относительно собственных центральных осей (см. формулы (5.10)–(5.17)):

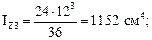
6. Вычисляем расстояния от центральных осей всего сечения Z и Y до центральных осей отдельных фигур (рис. 5.10):

так как оси Y₁, Y₂, Y₃ совпадают с осью симметрии Y.

7. Вычисляем осевые моменты инерции всего сечения относительно центральных осей Z и Y по формулам (5.9):

Центробежный момент инерции I_ZY всего сечения равен нулю, так как ось Y является осью симметрии, т.е. оси Z и Y являются главными центральными осями инерции сечения, а вычисленные осевые моменты инерции являются главными центральными моментами инерции:

ПРИМЕР 5.3

Требуется определить главные центральные моменты инерции составного сечения, показанного на (рис. 5.11).

РЕШЕНИЕ

Порядок решения подробно рассмотрен в примере 5.2.

1. Разбиваем сечение на отдельные фигуры, геометрические характеристики которых приводятся в таблице сортаментов (двутавр и швеллер) или легко вычисляются по формулам (5.10)–(5.20) (в данном примере прямоугольник) и проводим их центральные оси.

2. Проводим ось симметрии Y. Центр тяжести всего сечения лежит на этой оси.

3. Выбираем произвольную ось Z¢. Пусть в данном примере эта ось совпадает с осью Z₃.

4. Расстояние у_C определяем от произвольной оси Z¢ до центра тяжести всего сечения:

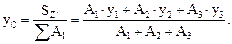
Расстояния от произвольно выбранной оси Z' до центральных осей каждой фигуры (у₁, у₂, у₃) показаны на рис. 5.11.

Площади сечений швеллера А₁ и двутавра А₂ выписываем из соответствующих таблиц сортамента, а площадь прямоугольника А₃ вычисляем:

А₁ = 23,4 см², А₂ = 46,5 см², А₃ = 24 2 = 48 см².

Отложим величину у_C вверх от оси Z' (так как у_C> 0) и на этом расстоянии проведем главную центральную ось Z.

5. Геометрические характеристики прокатных профилей выписываем из таблицы сортаментов, учитывая различие в ориентации осей в таблице сортаментов и на рис. 5.12а, в.

1. Швеллер № 20

ГОСТ 8240-89

(рис. 5.12а) ;

Двутавр № 30

ГОСТ 8239-89

(рис. 5.12б) h = 30 см.

Буква "с" в индексе осевых моментов инерции I означает ссылку на обозначение осей в сортаменте.

Моменты инерции прямоугольника (рис. 5.12в) вычисляем отдельно по формулам (5.10) и (5.11):

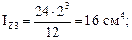
6. Определяем расстояния от общих центральных осей Y и Z до центральных осей отдельных фигур (они показаны на рис. 5.11):

так как оси Y₁, Y₂, Y₃совпадают с осью симметрии всего сечения Y.

7. Определяем осевые моменты инерции сложной фигуры относительно центральных осей Z и Y по формулам (5.9):

Центробежный момент инерции так как ось Y является осью симметрии. Поэтому оси Z и Y являются главными центральными осями.

Дата добавления: 2019-02-26; просмотров: 251; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒

Мы поможем в написании ваших работ!