Read the text and do the tasks below it.
Equivalent fractions
Multiplying the numerator and denominator of a fraction by the same (non-zero) number, the results of the new fraction is said to be equivalent to the original fraction. The word equivalent means that the two fractions have the same value. That is, they retain the same integrity – the same balance or proportion. This is true because for any number n, multiplying by  is really multiplying by one, and any number multiplied by one has the same value as the original number. For instance, consider the fraction
is really multiplying by one, and any number multiplied by one has the same value as the original number. For instance, consider the fraction  : when the numerator and denominator are both multiplied by 2, the result is
: when the numerator and denominator are both multiplied by 2, the result is 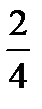 , which has the same value (0.5) as
, which has the same value (0.5) as  . To picture this visually, imagine cutting the example cake into four pieces; two of the pieces together (
. To picture this visually, imagine cutting the example cake into four pieces; two of the pieces together ( 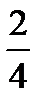 ) make up half the cake (
) make up half the cake (  ).
).
For example: 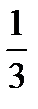 ,
,  ,
,  and
and  are all equivalent fractions.
are all equivalent fractions.
Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. This is called reducing or simplifying the fraction. A fraction in which the numerator and denominator have no factors in common (other than 1) is said to be irreducible or in its lowest or simplest terms. For instance,  is not in its lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,
is not in its lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,  is in lowest terms – the only number that is a factor of both 3 and 8 is 1.
is in lowest terms – the only number that is a factor of both 3 and 8 is 1.
Any fraction can be fully reduced to its lowest terms by dividing both the numerator and denominator by their greatest common divisor . For example, the greatest common divisor of 63 and 462 is 21, therefore, the fraction  can be fully reduced by dividing the numerator and denominator by 21:
can be fully reduced by dividing the numerator and denominator by 21:
 .
.
Reciprocals and the ‘invisible denominator’
The reciprocal of a fraction is another fraction with the numerator and denominator reversed. The reciprocal of  , for instance, is
, for instance, is  .
.
Since any number divided by 1 results in the same number, it is possible to write any whole number as a fraction by using 1 as the denominator: 17 =  (1 is sometimes referred to as the ‘invisible denominator’). Therefore, except for zero, every fraction or whole number has a reciprocal. The reciprocal of 17 is
(1 is sometimes referred to as the ‘invisible denominator’). Therefore, except for zero, every fraction or whole number has a reciprocal. The reciprocal of 17 is  .
.
In pairs, look at the highlighted words and phrases. Try to guess what they mean from the context. Then check with your dictionary or teacher. Work out the list of the terms involved, make a kind of glossary.
2. In the text find the definition of:
a. equivalent fractions
|
|
|
b. reducing a fraction
c. irreducible fraction
d. reciprocal
Explain what fractions out of these seven are equivalent.

| 
| 
| 
| 
| 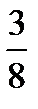
| 
|
Say if the following fractions are reducible or in their lowest terms. Explain why.

| 
| 
| 
| 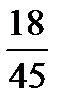
|
Unit 7
ALGEBRA
Reading and Vocabulary
1. Match the definitions/explanations in A (1–5) with the words in B (a-e):
Дата добавления: 2019-02-26; просмотров: 266; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
