Корректирующие устройства САР.
К корректирующим средствам относятся, в частности, корректирующие звенья, представляющие собой динамические звенья с определенными передаточными функциями.
В случаях, когда корректирующие звенья используются именно для повышения устойчивости автоматической системы или для обеспечения ее запаса устойчивости, они называются иногда демпфирующими или стабилизирующими звеньями. При этом имеется в виду, что звенья демпфируют колебания, которые возникают в автоматической системе.
Термин "корректирующие звенья" является более широким и используется для звеньев, которые вводятся в автоматическую систему для изменения ее статических или динамических свойств с различными целями.
Получение требуемого быстродействия обычно обеспечивается при проектировании автоматической системы посредством выбора соответствующих элементов системы регулирования. Однако возможно улучшение быстродействия автоматической системы посредством использования корректирующих средств.
Косвенные методы оценки качества регулирования.
Качество любой системы регулирования определяется величиной ошибки:
x(t)=g(t)−y(t)=Φx(p)g(t)
Но функцию ошибки x(t) для любого момента времени трудно определить, поскольку она описывается с помощью ДУ системы – Φx(p) – высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САР по некоторым ее свойствам, определяют которые с помощью критериев качества.
|
|
|
Критериев качества регулирования много. Их разделяют на 4 группы:
Критерии точности – используют величину ошибки в различных типовых режимах.
Критерии величины запаса устойчивости – оценивают удаленность САР от границы устойчивости.
Критерии быстродействия – оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.
Интегральные критерии – оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.
Линеаризация нелинейных функций.
Под линеаризацией понимается замена нелинейных дифференциальных уравнений линейными уравнениями, которые с достаточной для практики точностью описывают физические процессы в САУ. Признаком, позволяющим произвести линеаризацию уравнений с математической точки зрения, является отсутствие разрывных, неоднозначных или резко изменяющихся характеристик, определяющих зависимость переменных уравнений от различных факторов, т.е. существование производных функций по всем переменным. Физической предпосылкой линеаризации является малая величина отклонений переменных в уравнениях элементов от их установившихся значений в силу самого принципа работы замкнутой автоматической системы, в состав которой эти элементы входят.
|
|
|
Сущность линеаризации в том, что все нелинейные функции одной или нескольких переменных, входящих в уравнение элемента, разлагают в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму, по степеням отклонений. Так, формула Тейлора для нелинейной функции двух переменных x и y имеет следующий вид:
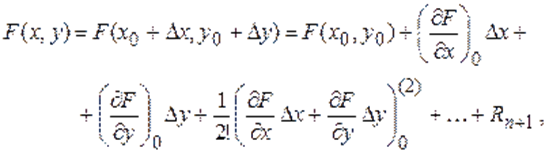
Логарифмические частотные характеристики.
При практических расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (логарифмические частотные характеристики – ЛЧХ). Они характеризуются большей линейностью и на определенных участках изменения частот могут быть заменены прямыми линиями и в целом представлены ломаными линиями. Причем отрезки прямых в большинстве случаев можно построить при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, т.к. умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.
Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют такое представление фазочастотной характеристики (ФЧХ), в котором частота выражена в логарифмическом масштабе.
Дата добавления: 2019-02-22; просмотров: 486; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
