Вычисление передаточной функции стационарной линейной системы
Передаточная функция системы определяется по ее дифференциальному уравнению при помощи преобразования Лапласа.
Уравнение (5.3) можно привести к следующему виду
Уравнение связывает изображение выходного сигнала системы с изображением входного сигнала и начальным состоянием системы. Функция W(s) характеризует динамические свойства системы. Она не зависит от входного сигнала и полностью определяется параметрами системы. Эту функцию называют передаточной функцией.
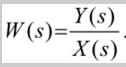
Поэтому передаточной функцией W(s) системы называется отношение изображения У(х) выходного сигнала к изображению А"(х) входного сигнала при условии, что все начальные условия равны нулю. Для систем, описываемых обыкновенным дифференциальным уравнением, передаточная функция является дробно-рациональной функцией относительно оператора преобразования Лапласa.
Д-разбиение для одной переменной
Метод D- разбиения
Используется при синтезе систем для определения допустимых по условиям устойчивости пределов изменения некоторых параметров системы (обычно к – коэф усил., или Т – регулятора).
Процесс построения в пространстве параметров (коэффициентов) областей с разным распределением корней ХУ называется D – разбиением.
Методика выполнения D-разбиения по одному параметру:
1) разрешаем хар-ое уравнение относит. исслед. пар-ра
2) заменим р на jω, выделяя веществ. и мнимые части
|
|
|
3) строим границу D-разбиения, изменяя ω от – ¥ до + ¥ ,
4) наносим штриховку границы и вычисляем распределение корней в какой-либо точке.
5) находим распределение корней во всех областях и выявляем область устойчивости.
Дифференциальное уравнение линейной астатической системы автоматического регулирования
Дифференциальное уравнения линейной статической системы автоматического регулирования
Дифференцирующие звено
Дифференцирующее звено реализует функцию дифференцирования входного сигнала. Для этого звена выходной сигнал пропорционален скорости изменения входного сигнала. Уравнение дифференцирующего звена
переходная характеристика для дифференцирующего звена представляет собой усиленную в k раз импульсную дельта-функцию
Уравнение звена в операторном виде
,
откуда передаточная функция звена
.
Частотная функция дифференцирующего звена
,
при этом 
, 
Д- разбиение для двух переменных
Рассмотрим случай, когда два параметра П1 и П2 входят в состав коэффициентов характеристического полинома линейно. тогда
D(p) = D0(p) + П 1 D1(p) + П 2 D2(p) = 0.
Определим значения П1 и П2, при которых уравнение имеет пару чисто мнимых корней рi,i+1=±jωi. Для этого подставим р=jωi,- в уравнение, получим:
|
|
|
D(jωi) = П1D1(jωi) + П2D2 ( jωi) + D0( jωi) = 0.
Это уравнение распадается на два:
П2Р1(ωi)+П1Q1(ωi)=-R1(ωi)
П2Р2(ωi)+П1Q2(ωi)=-R2(ωi)
Заметим, что в полученных уравнениях первыми стоят члены с параметром П2, и именно этот параметр должен откладываться по горизонтальной оси.
Запаздывающее звено
Уравнение запаздывающего звена представляется в следующем виде: y(t) = x(t - τ)
где τ - является временем запаздывания. При нулевых начальных условиях это уравнение принимает в операторной форме следующий вид: Y (р) = X (р)℮-pt
Передаточная функция запаздывающего звена будет выглядеть, как: W(p)= ℮-pt
АФЧХ запаздывающего звена выражается в виде: W(jω) = Re(ω) + Im(ω) = A(ω)℮ jj(w)= cos ωτ - j sin ωτ
на основании данного выражения определим АЧХ и ФЧХ запаздывающего звена: A (ω) = 1; j ( w ) = arctg ( - sin ωτ/ cos ωτ) = - ωτ
Переходная функция запаздывающего звена представлена в виде: h(t) = 1(t − τ)
Импульсная переходная характеристика имеет следующее значение: w(t) = h′(t) = δ (t −τ )
Запасы устойчивости
Для нормального функционирования САР должна быть достаточно удалена от границы устойчивости и иметь достаточный запас устойчивости, что определяется следующими причинами:
|
|
|
- уравнения элементов САР, как правило, идеализированы, т.е. при их составлении не учтены второстепенные факторы;
- при линеаризации уравнений погрешности дополнительно увеличиваются;
- параметры элементов определяются с некоторой погрешностью;
- параметры однотипных элементов имеют технологический разброс;
- при эксплуатации параметры элементов изменяются вследствие старения.
О запасе устойчивости можно судить по расположению корней характеристического уравнения САР на комплексной плоскости корней. Чем дальше они от мнимой оси в левой полуплоскости, тем больше запас устойчивости.
Запас устойчивости по амплитуде h – это минимальный отрезок, характеризующий расстояние между критической точкой и ближайшей точкой пересечения годографом Найквиста вещественной оси на отрезке [0, -1]. Запас устойчивости по фазе g - это минимальный угол, образуемый радиусом, проходящим через точку пересечения годографа Найквиста с окружностью единичного радиуса с центром в начале координат и отрицательной вещественной полуосью.
Звенья второго порядка
|
|
|
Звеном второго порядка называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида
где Т – постоянная времени ; ξ – относительный коэффициент затухания.
Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
В зависимости от вида корней характеристического уравнения инерционное звено второго порядка может иметь различные переходные характеристики. Это позволяет установить три разновидности звена – апериодическое, колебательное и консервативное.
При единичном входном воздействии для случая вещественных различных корней р1 и р2по уравнению получим переходную функцию (ξ≥1):
В случае вещественных корней апериодическое звено второго порядка эквивалентно последовательному соединению двух инерционных звеньев первого порядка, поэтому передаточная функция может быть записана в виде
По выражению W(p) после замены р на jω получим частотную функцию W(jω) апериодического звена второго порядка, которая определяет частотные характеристики звена.
Звенья первого порядка
К звеньям первого порядка относятся инерционное звено первого порядка, форсирующее звено, инерционно-дифференцирующее звено, инерционно-форсирующее звено.
Инерционными звеньями первого порядка являются конструктивные элементы, которые могут накапливать и передавать энергию или вещество. Форсирующим звеном называют звено, которое описывается уравнением. или, что то же, передаточной функцией. Это звено, как и апериодическое, характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом.
Звено называют инерционно- дифференцирующим, если сумма выходной координаты и скорости ее изменения прямо пропорциональна скорости изменения входной координаты.
Форсирующее звено - Выходная величина этого звена пропорциональна входной и производной от входной величины.
Дата добавления: 2019-02-22; просмотров: 424; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!