Амплитудно-фазовый критерий устойчивости Найквиста

⇐ ПредыдущаяСтр 2 из 17Следующая ⇒

Критерий Найквиста позволяет оценивать устойчивость замкнутой системы автоматического управления по частотным характеристикам разомкнутой системы. В качестве частотных характеристик используется амплитудно-фазовая (АФХ) характеристика и ЛАФЧХ разомкнутой системы.

Рассмотрим сначала критерий Найквиста на базе АФХ разомкнутой системы.

Пусть передаточная функция разомкнутой системы

Передаточная функция замкнутой системы

где A(s) + B(s) = D(s) - характеристический полином замкнутой системы.

Рассмотрим вспомогательную функцию

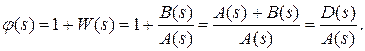
Заметим, что числитель j(s) равен D(s) характеристическому полиному замкнутой системы, а знаменатель A(s) - характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m £ n.

Анализ устойчивости по логарифмическим частотным характеристикам

В том случае, когда АФЧХ не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие w_с< w_кр. То есть замкнутая система будет абсолютно устойчивой, если ЛАХ разомкнутой системы принимает отрицательные значения раньше, чем ЛФХ достигнет значения фазы -180⁰. Если ЛАХ разомкнутой системы принимает отрицательные значения позже, чем ЛФХ достигнет значения фазы -180⁰, то замкнутая система неустойчивая. Если ЛАХ разомкнутой системы принимает значение амплитуды 0 дб на одной частоте, что и ЛФХ достигнет значения фазы -180⁰, то это соответствует колебательной границе устойчивости.

По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе m отсчитывается по ЛФХ на частоте среза w_с, а запас по амплитуде L_h соответствует значению ЛАХ на критической частоте w_кр, взятому с обратным знаком. 20 lg k _гр = 20 lg k + L_h , где k - общий коэффициент передачи разомкнутой системы.

Анализ устойчивости систем с запаздыванием

Так как характеристическое уравнение САР с запаздыванием (6) является трансцендентным, то применение алгебраических критериев является достаточно сложным. Поэтому для анализа САР с запаздыванием в работе используются частотные критерии Михайлова и Найквиста.

Характеристический полином для САР с запаздыванием определяется выражением

Заменив p на jw, получим

Выделив вещественную и мнимую части выражения (8), можно записать:

Каждая часть выражения (9) содержит колебательные по характеру составляющие, что отражается на форме годографа Михайлова.

Для устойчивости САР с запаздыванием по критерию Михайлова необходимо и достаточно, чтобы годограф Михайлова при изменении частоты w от 0 до +¥ повернулся в положительном направлении (против часовой стрелки), начиная с вещественной положительной полуоси, на число квадрантов, равное порядку характеристического уравнения, то есть на угол np/2, при этом нигде не обращаясь в нуль.

Для устойчивости САР с запаздыванием по критерию Найквиста необходимо и достаточно, чтобы при изменении частоты w от 0 до +¥ годограф Найквиста не охватывал точку с координатами (-1, j0).

Годограф Найквиста для САР с запаздыванием строится следующим образом.

Сначала строят годограф Найквиста для САР без запаздывания, заменив в выражении (3) p на jw. Годограф Найквиста для САР без запаздывания приведен на рисунке 3 (кривая ). Затем каждый вектор, соответствующий частоте , поворачивается на угол . И так для всех частот от 0 до +¥. В итоге получается годограф Найквиста для САР с запаздыванием.

Безынерцонное звено

Безынерционным звеном называется такое звено, в которой исходная величина в пропорциональна входной х, то есть исходная величина воспроизводит без искажений и
запаздываний входную величину у = kx, где k — коэффициент преобразования или коэффициент передачи цепи. Переходный процесс в такой звене отсутствует. В этом звене скачкообразное изменение входной величины мгновенно передается на выход звена.
Передаточная функция безынерционной звена W (p) = k.
Примерами безынерционных звеньев является механический редуктор, потенциометр, механические пружины, электронная усилительная лампа, полупроводниковый триод, сельсины, трансформатор, жесткий рычаг и др.

Весовые функции

Весовая функция — математическая конструкция, используемая при проведении суммирования, интегрирования или усреднения с целью придания некоторым элементам большего веса в результирующем значении по сравнению с другими элементами.

Весовая функция ω(t) – это реакция системы на входное воздействие типа дельта функции (функции Дирака). δ(t)=x(t) ω(t)=Y(t) при x(t)=δ(t) при - дельта – функции (функции Дирака) - А→ ∞ - → 0

Весовая функция Сигнал, полученный на выходе линейной САУ при подаче на её вход единичного импульса (t), называется весовой (или импульсной переходной) функцией W(t). Весовая функция – оригинал передаточной функции.

Виды процессов управления

Виды процессов управления. В различных условиях процесс управления может быть построен различными способами при сохранении всех его специфических свойств. Это позволяет классифицировать процессы управления, выделить их наиболее типичные виды:
• линейный (характеризуется строгой последовательностью осуществления его этапов и используется тогда, когда есть полная и достаточная определенность относительно цели воздействия, ситуации и т. д.);
• корректируемый (предполагает необходимость дополнительной корректировки каждого из этапов процесса управления после прохождения последующего этапа);
• разветвленный (заключается в методологическом разделении работ по частям на определенных этапах);
• ситуационный (характеризуется тем, что возникает как бы в зависимости от ситуации, при которой из нее же главным образом исходят и поиск проблемы, и разработка решения);
• поисковый (исходит из полной ясности цели воздействия, но при этом невозможно оценить ситуацию и сформулировать проблему. В этом случае решение разрабатывается на основе цели и наиболее общей оценки ситуации, и уже на основе решения уточняется ситуация).

Воздействия в САУ

Прикладываемые к САУ внешние воздействия можно разделить на задающие и возмущающие.

Задающие воздействия определяются тем законом, по которому должна изменяться управляемая величина.Если управляемая величина должна изменяться по некоторой программе – задающее воздействие будет некоторой заранее заданной функцией времени. Вид задающего воздействия может быть различным, и он определяется условием работы системы.

Возмущающее воздействие можно разделить на нагрузку и помехи.

Нагрузкой является внешнее воздействие, приложенное к объекту управления, не зависящее от управляющего устройства и обусловленное нормальной работой этого объекта.

Помехи – это внешние воздействия, преложенные к отдельным элементам системы и не связанные с ее нормальной работой.

В качестве типовых воздействий на практике наиболее часто используют следующие:

1.Единичная ступенчатая функция. Это воздействие применяют, когда процесс регулирования вызван резким изменением нагрузки или быстрым изменением задающей величины

2.Дельта-функция. Это воздействие применяют, когда процесс регулирования вызван мгновенным “толчком”

3.Гармоническое воздействие

4.Воздействия, изменяющиеся с постоянной скоростью

5.Воздействия, изменяющиеся с постоянным ускорением

Временные характеристики

Временной характеристикой системыназывается закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.

К основным временным характеристикам относятся переходная функция и функция веса.

Реакция системы (элемента) автоматического управления на единичную ступенчатую функцию при условии, что система до приложения воздействия находилась в покое, называется переходной функцией h(t).

Переходную функцию можно получить как решение неоднородного дифференциального уравнения системы, правой частью которого является единичная ступенчатая функция. Выражение для переходной функции будет иметь вид

Реакция САУ на единичную импульсную функцию при условии, что система до приложения воздействия находилась в покое, называется весовой функцией

Выделение областей устойчивости

При помощи критерия устойчивости устанавливается факт устойчивости или неустойчивости САР, все параметры которой заданы.

Допустимые пределы варьирования параметров системы можно определить путем построения области устойчивости. Областью устойчивости называется область в пространстве варьируемых параметров, каждой точке которой соответствуют только левые корни характеристического уравнения. Область устойчивости выделяет из всех возможных значений параметров лишь те значения, при которых САР устойчива. Поверхность, ограничивающая область устойчивости называется границей области устойчивости.

Граница области устойчивости в принципе может быть найдена путем многократного применения одного из критериев устойчивости, при различных значениях варьируемых параметров.

Если часть корней характеристического уравнения находится на мнимой оси, а остальные корни — в левой полуплоскости, то считают, что система находится на границе устойчивости. Значения параметров, при которых система находится на границе устойчивости, называются граничными.

При использовании алгебраических критериев нужно исходить из условия, что система находится на границе устойчивости, если часть коэффициентов и определителей равна нулю, остальная часть – больше нуля.

Дата добавления: 2019-02-22; просмотров: 338; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!