Алгебраические методы устойчивости
D -разбиение Пусть система описывается характеристическим уравнением n-ой степени: A(p) = an p^n +an-1 p^n-1 +an-2 p^n-2 + … + a0 = 0 При заданных коэффициентах уравнение имеет определённые корни, пусть m – в правой полуплоскости; (n - m) – корни в левой полуплоскости. При изменении коэффициентов корни перемещаются в плоскости корней. Это перемещение называется корневым годографом. При некотором сочетании коэффициентов корень может попасть в начало координат или на мнимую ось, тогда значения коэффициентов подчиняются характеристическому уравнению (an = 1): A ( j ω ) = ( j ω ) n + an -1 ( j ω ) n -1 + … + a0 = 0 Это уравнение в (n-1)– мерном пространстве коэффициентов, по осям которого отложены а0 …аn-1 при заданном значенииω соответствует точка, а при измененииω – гиперповерхность. Если изменять коэффициенты, то при некотором сочетании их произойдет пересечение гиперповерхности А(jω ) = 0, следовательно, один или пара мнимых корней перейдет из правой (левой) полуплоскости в левую (правую) полуплоскость. Наиболее простой вариант, когда степень характеристического уравнения не превышает трех (n≤ 3). Разбиение по одному комплексному параметру. Для выяснения влияния какого-либо параметра на устойчивость системы, придерживаются следующего алгоритма: Представить характеристическое уравнение в виде А(р) = Р(р) + ϑQ(р), где: ϑ - исследуемый параметр. Определить границы D-разбиения, для этого заменить р на jω : А(jω ) = Р(jω ) +ϑ Q(jω ). Выразить параметр ϑ из уравнения границы D-разбиения и представить его в алгебраической форме комплексного числа ϑ = -P (jω ) = Х + jY Q (jω ) Изменяя ω от 0 до +∞ , построить половину границы. В силу симметричности относительно действительной оси границы D-разбиения построить вторую половину границы, соответствующую изменению ω от -∞ до 0. Провести штриховку полученной границы слева при движении по границе в сторону увеличения частоты. Определить устойчивость системы в области с внутренней штриховкой, выбирая самое простое значение ϑ , например ϑ = 0.
|
|
|
Алгебраические критерии устойчивости
Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:
1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;
2) во второй строке - с нечетными;
3) остальные элементы таблицы определяется по формуле: ck,i = ck+ 1,i - 2 - ri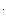 
ck + 1,i - 1, где ri = c1,i - 2/c1,i - 1, i 
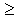3 - номер строки, k - номер столбца.
4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
|
|
|
Критерий Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица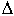 
по алгоритму:
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an;
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.
Алгебраические методы устойчивости
Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:
1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;
2) во второй строке - с нечетными;
3) остальные элементы таблицы определяется по формуле: ck,i = ck+ 1,i - 2 - ri 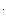ck + 1,i - 1, где ri = c1,i - 2/c1,i - 1, i 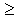3 - номер строки, k - номер столбца.
|
|
|
4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Критерий Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица 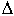по алгоритму:
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an;
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.
Дата добавления: 2019-02-22; просмотров: 508; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!