Эквивалентная схема электроприёмника
Любой электроприёмник можно представить эквивалентной схемой, состоящей из активного, индуктивного и ёмкостного элементов. Такая схема изображена на рис. 1.4.1, а. Как видно из схемы рис.1.4.1, а напряжение приложено ко всем трём элементам, соединённым параллельно.
Рисунок 1.4.1 – Цепь с активным, индуктивным и ёмкостным элементами: а – схема включения, б – векторная диаграмма, в – треугольник сопротивлений
Для схемы рис. 1.4.1, а построена векторная диаграмма (рис.1.4.1, б). Ток в цепи с индуктивностью отстаёт от напряжения на угол 
, значение которого определяется из треугольника сопротивлений, изображённого на рис. 1.4.1, г, где 
. Ток в цепи с активным сопротивлением совпадает по фазе с приложенным напряжение, а ток в цепи с конденсатором опережает напряжение на 90˚. В схеме (рис.1.4.1, а) 
, соответственно, результирующий ток будет отставать от напряжения на угол φ. Из векторной диаграмм (рис.1.4.1, б) следует, что эквивалентную схему можно представить в виде простой цепи, состоящей из эквивалентных сопротивлений R΄ и 
(рис.1.4.2, а), для которой векторная диаграмма и треугольник сопротивлений представлены на рис. 1.4.2, б и рис. 1.4.2, в.
Рисунок 1.4.2 – Цепь с активно-индуктивными элементами: а – схема замещения, б – векторная диаграмма, в – треугольник сопротивлений.
В схеме замещения (рис.1.4.2, а) является результатом компенсации части индуктивного сопротивления за счёт действия ёмкостного элемента
|
|
|
. (17)
Мгновенная мощность, потребляемая электроприёмником (рис. 1.4.2, а), равна:
, (18)
где 
– мгновенная мощность резисторного элемента,
– мгновенная мощность реактивного сопротивления.
Из векторной диаграммы рис. 1.4.2, б видно, что 
, а 
, т.е. активную мощность можно представить как 
, а реактивную - 
, чему соответствует треугольник мощностей, изображённый на рис. 1.4.3.
Рисунок 1.4.3 – Треугольник мощностей
Отношение реактивной мощности Q к активной P называется коэффициентом реактивной мощности
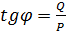. (19)
Данная величина показывается долю реактивной мощности от активной и является одним из критериев качества электрической энергии.
Коэффициент мощности определяется косинусом сдвига фаз между током и напряжением и выражается как
, (20)
где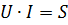 
– полная (предельная) мощность.
Полная мощность S является геометрической суммой активной и реактивной мощностей и определяется как
(21)
На рис. 1.4.4 изображены графики изменения мгновенных значений полной, активной и реактивной мощностей для схемы замещения, изображённой на рис. 1.4.2, а.
|
|
|
Рисунок 1.4.4 – График изменения мгновенный значений мощностей
Из графиков рис. 1.4.4 следует, что в течение интервала времени 
мгновенная мощность, а также её составляющие 
и 
положительны, т.е. энергия от источника преобразуется в сопротивлении R΄ в тепло, а частично в энергию магнитного поля в катушке индуктивности. В течение интервала времени 
мгновенная и активная мощности приёмника положительные, а реактивная мощность отрицательная, т.е. в сопротивлении R΄ энергия, передаваемая от источника и частично от запасённой энергии в катушке, преобразуется в тепло. В течение интервала времени 
реактивная мощность , превосходящая по абсолютной величине положительную мощность , отрицательная, т.е. энергия магнитного поля, запасённая в катушке, передаётся от приёмника генератору и частично преобразуется в тепло в сопротивление R΄.
Из выше сказанного следует, что в сопротивление R΄ энергия преобразуется в тепло не только за счёт протекания тока активной составляющей мощности, но и за счёт обмена энергией между генератором и магнитным полем, т.е. при обмене энергией возникают дополнительные потери активной мощности.
|
|
|
Дата добавления: 2019-02-22; просмотров: 170; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!