Базис совокупности векторов.Базиа на плоскости и в пространстве.Единственность разложения вектора в заданном базисе.






Координаты вектора, их арифметическое свойство.Ортонормированнвй базис.Орт оси.
Определение1. Арифметическим п - мерным вектором называется любая последовательность из п действительных чисел 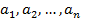 .
.
Краткая запись 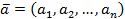 . Числа
. Числа  называются координатами вектора. Например, вектор
называются координатами вектора. Например, вектор  имеет координаты 0, -2, 1, 5.
имеет координаты 0, -2, 1, 5.
Геометрически можно изобразить только одномерные (направленные отрезки на прямой), двумерные (на плоскости), трёхмерные (в пространстве) арифметические векторы.
Определение 2.Два вектора 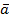 и
и  с одним и тем же числом координат
с одним и тем же числом координат 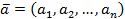 ,
,  будем считать равными в том и только том случае, когда
будем считать равными в том и только том случае, когда  Равенство векторов обозначается обычным образом
Равенство векторов обозначается обычным образом  .
.
Определение 3. Суммой двух векторов  называется вектор
называется вектор
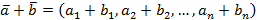 .
.
Вектор 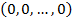 называется нулевым и обозначается
называется нулевым и обозначается  . Вектор
. Вектор  называется противоположным вектору
называется противоположным вектору  и обозначается
и обозначается  .
.








1.  .
.
2.  .
.
3. 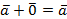 .
.
4.  .
.
Определение 4. Произведением вектора 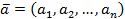 на число k называется
на число k называется
вектор
 .
.



|

5.  .
.
6. 
7. 
8. 







27 . Скалярное произведение векторов, его свойства, вычисление в ортонормированном базисе





Приложение скалярного произведения.Геометрический смысл координат вектора в ортонормированном базисе.Направляющие косинусы вектора





ПРАВАЯ И ЛЕВАЯ ТРОЙКА ВЕКТОРОВ.ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ,ЕГО СВОЙСТВА, ВЫЧИСЛЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
|
|
|
ОПРЕДЕЛЕНИЕ
Упорядоченная тройка векторов называется правой, если из конца третьего вектора поворот от вектора к вектору по наименьшему углу происходит против часовой стрелки (рис. 1), и левой – если поворот по наименьшему углу происходит по ходу часовой стрелки (рис. 2).


Замечание. Правая тройка векторов также называется еще положительно ориентированной, а левая – отрицательно ориентированной.
Замечание. Перестановка двух соседних векторов в рассматриваемой тройке меняет ее ориентацию.
Замечание. Циклическая перестановка или ориентацию тройки не меняет.
Утверждение. Тройка векторов является правой тогда и только тогда, когда смешанное произведение этих векторов больше нуля; и левой – если смешанное произведение меньше нуля.
Определение. Векторным произведением вектора 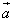 на вектор
на вектор  называется вектор
называется вектор  , обозначаемый символом
, обозначаемый символом  и удовлетворяющий следующим трём требованиям:
и удовлетворяющий следующим трём требованиям:
1) длина вектора  равна произведению длин векторов
равна произведению длин векторов 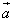 и
и  на синус угла
на синус угла  между ними, то есть
между ними, то есть
 ;
;
2) вектор  ортогонален к каждому из векторов
ортогонален к каждому из векторов 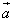 и
и  ;
;
3) вектор  направлен так, что тройка векторов
направлен так, что тройка векторов  является правой.
является правой.
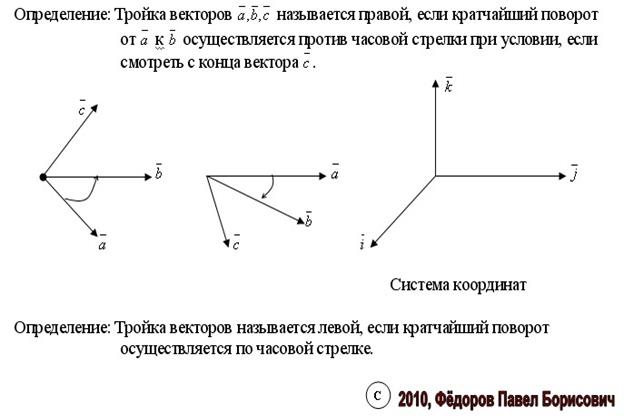


30. Смешанное произведение трех векторов, его геометрический смысл, свойства, вычисление в ортонормированном базисе трехвекторов 
|
|
|






Использование ортонормированных базисов облегчает вычисление скалярного произведения по координатам векторов. Пусть в евклидовом пространстве Ε задан некоторый базис е = (e1 ... еn). Рассмотрим два произвольных вектора х и у в этом пространстве. Эти векторы представляются в базисе е своими координатами:
х = x1e1 + ... + хnеn, у = y1e1 + ... + ynen.
Запишем эти разложения векторов по базису в матричной форме:

Скалярное произведение векторов х и у может быть выражено через скалярные произведения векторов базиса:

Составив из скалярных произведений базисных векторов ква-дратную матрицу Г = ((ei,ej)) порядка n, мы можем записать скалярное произведение заданных векторов в матричной форме:
(x,y) = xTГy.
Матрица Г является симметрической в силу коммутативности операции скалярного умножения. Ее называют матрицей Грама системы векторов e1, ..., еn.
Пусть базис е является ортонормированным. Тогда скалярное произведение (еi, еj) при несовпадающих i и j равно нулю, а скалярные квадраты базисных векторов равны e2i = ||еi||2 = 1. Это значит, что для ортонормированного базиса матрица Г является единичной. Поэтому
|
|
|
(x, у) = хTЕу = xTу = x1y1 + x2y2 + ... + xnуn.
В частности, в ортонормированием базисе норма вектора х, которая выражается через скалярный квадрат этого вектора, может быть вычислена по формуле
||x|| = √(х,х) = √(х21 + ... + х2n) = √(xTx), (3.7)
а для косинуса угла φ между ненулевыми векторами х и у получаем выражение
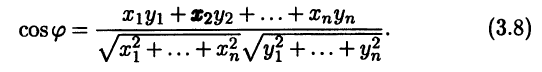
В ортонормированном базисе e1, ..., еn также упрощается вычисление координат вектора: они выражаются через скалярные произведения. Бели х = x1e1 + ... + хnеn, то, умножив равенство скалярно на вектор еi, находим, что
(х, еi) = xi, i = 1,n.
Пример 3.13. В евклидовом арифметическом пространстве R4 найдем угол между векторами а = (-1, 1, 0, 2) и b = (2, -1, 1, 0). Согласно формуле (3.8),

Условия коллинеарности, ортогональности, компланарности в ортонормированном базисе.
Определение.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
Дата добавления: 2019-02-22; просмотров: 1564; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
