В третьем случае необходимы дополнительные исследования
19..Выпуклость графика функции :достаточное условие.
20.Точки перегиба: достаточное условие.
21. Наклонные асимптоты кривой: необходимое и достаточное условие. ВЕртикальнае асимптоты.
Прямая L : y = kx + b является наклонной асимптотой графика функции
y = f ( x ) тогда и только тогда, когда существуют конечные пределы:
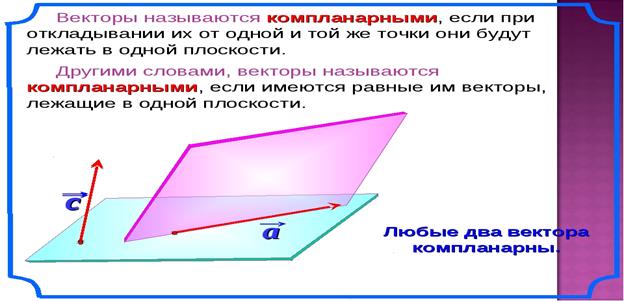
Угол между векторами. Проекция вектора на вектор, ее свойства.
Под углом между векторами понимается угол между векторами равными данным и имеющими общее начало. Если направление отсчета угла не указано, то углом между векторами считается тот из углов, который не превосходит π. Если один из векторов нулевой то угол считается равным нулю. Если угол между векторами прямой то векторы называются ортогональными.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначения: коллинеарность векторов записывают привычным значком параллельности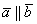 
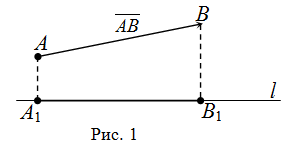
Проекцией вектора на ось называется число, которое равно величине отрезка , принадлежащего указанной оси, где точки и – проекции точек и на рассматриваемую ось соответственно (рис. 1).
ОПРЕДЕЛЕНИЕ
Проекцией вектора на направление вектора , называется число, которое равно величине проекции вектора на ось , проходящую через второй вектор (рис. 2).
Проекция вектора на направление вектора равна скалярному произведению этих векторов, деленному на длину вектора :
|
|
|
Проекции векторов обладают следующими свойствами:
-
(проекция суммы равна сумме проекций); -
(проекция произведения вектора на число равна произведению проекции вектора на число).
Линейная зависимость и независимость системы векторов. Необходимое и достаточное условие линейной зависимости, следствие.Теорема о системе, содержавшей нулевой вектор.
Понятие линейной комбинации векторов
Линейная комбинация - это сумма векторов, умноженных на некоторые числа . Эти векторы могут иметь разное направление.
То есть, линейная комбинация - это выражение вида
,
где 
- какие угодно вещественные числа.
Теорема о системе, содержавшей нулевой вектор.
Длина нулевого вектора равна нулю:
С нулевым вектором не связано никакое направление в пространстве. Нулевой вектор считается сонаправленным любому вектору. Нулевой вектор одновременно коллинеарен и ортогонален любому вектору пространства.
Все координаты нулевого вектора в системе координат равны нулю. Например, в трехмерном пространстве
допустим есть какая то система векторов, содержащая нулевой вектор.
рассмотрим их линейную комбинацию
α1*x1 + α2*x2 + α3*x3 = 0 (этого хватит)
пусть x1 =0
α1*x1 = -α2*x2 -α3*x3
пусть α1 не равно нулю.
тогда можно поделить на α1.
0=x1 = -α2/α1*x2 -α3/α1*x3
можно взять α2=α3=0
|
|
|
если имеется хотя бы одно число α , не равное нулю, и при этом линейная комбинация обращается в нуль, то
система линейно зависима
Дата добавления: 2019-02-22; просмотров: 387; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!