Или хотя бы одна из этих производных не существует.

Производная функция Дифференцируемость и не дифференцируемость функций Производная функции (в точке) — это понятие дифференциального исчисления, которое характеризует скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, которая имеет конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). - - правая производная - - левая производная Критерий ∃ производной: Физический смысл производной функции. : s'(t)=v(t) v'(t)=a(t), где s(t) -пройденный путь; v(t) - скорость; a(t) - ускорение. – Математическое определение производной функции в заданной точке X. Читается это определение так: Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. то отношение показывает, на сколько единиц В среднем изменится Y, если X изменится на единицу длины участка . То есть отношение определяет Среднюю скорость изменения функции на участке оси Ох. . Пусть функция определяет Закон движения некоторой материальной точки по траектории ее движения, где X – время, а Y – координата точки на траектории   Если X – время, а Y – координата движущейся точки на траектории ее движения (рис. 4.3), то функция определяет закон движения точки, а производная этой функции – мгновенную скорость движения точки по ее траектории: В этом состоит Физический смысл производной функции.     Но у производной функции есть и наглядный Геометрический смысл. Для его выяснения рассмотрим рис.4.4. Проведем к графику функции через точку и точку секущую , а через точку Касательную L. Их углы наклона к оси Охобозначим соответственно и . Из следует: (1.8) Если устремить к нулю, то и устремится к нулю, а точка N устремится к точке M. Соответственно секущая устремится к касательной L, проведенной в точке M, а угол наклона секущей устремится к углу наклона касательной. То есть при . Но тогда при Иначе говоря, , Что с учетом  дает То есть Производная функции в точке X – это угловой коэффициент касательной, проведенной к графику функции в точке графика с абсциссой X (см. рис. 4.5). В этом и состоит Геометрический смысл Производной функции.         Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование. Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — помогут таблица производных и правила дифференцирования, то есть правила нахождения производной. Основные правила дифференцирования 1) С = 0, С - cons t; 2) (u±v)' =u'±v', u(х), v(x) - дифференцируемые функции; 3) (u - v) = u' · v + u · v’, С · u = (С · u)'; 4) 5) дифференцирование сложной функции: если у = ƒ(u), где u = φ(х), то y'x=ƒ'u · u'x; 6) дифференцирование обратной функции: Пример: у = ln(х3 - Зх2)   2. Связь между дифференцируемостью и непрерывностью функций   Теорема. Если функция дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано. Доказательство. Пусть функция Дифференцируема в точке X. Это значит, что ее производная существует и конечна в точке X. То есть Существует и конечен. По определению предела это значит, что при . То есть при малых имеем , откуда , причем это приближенное равенство тем точнее, чем меньше . Устремляя в нем , получаем, что и . А это и означает непрерывность функции в точке X. Первая часть теоремы доказана. Обратно, если функция непрерывна в некоторой точке X, то это еще не значит, что она дифференцируема в этой точке. Например, функция непрерывна в любой точке X, ибо её график сплошной (без разрывов). И тем не менее в точках X1, X2 и X3, как было показано выше, она не дифференцируема.     3.Теоремы о дифференцируемости некоторых элементарных функций: y = C , Y =^2, y = lnx , Y = sinx

Теоремы о дифференцируемых функциях

1. Теорема. Ролля. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g(a)=g(b)=0, то существует по крайней мере одна точка a < c < b в которой производная g¢ обращается в нуль g¢(c)=0.

Доказательство. Так как функция непрерывна на [a,b], то она имеет на этом отрезке наибольшее (M) и наименьшее значение m. Пусть g(c) - наибольшее значение.

Отсюда

g(c+Dx) - g(c) Dx £ 0, Dx > 0

g(c+Dx) - g(c) Dx ³ 0, Dx < 0

Переходим к пределу и получаем одновременно g¢(с) ³ 0 и g¢(с) £ 0, следовательно, g¢(с)=0.

Пример функции, для которой не выполняется условие теоремы, поэтому производная внутри отрезка в 0 не обращается

y=1-(x2)1/3

2. Теорема. Лагранжа. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство

g(b)-g(a)=g¢(c)(b-a)

3. Доказательство. Применим теорему Ролля к функции

g(x)-g(a)-(x-a)Q,

4. где

Q=(g(b)-g(a))/(b-a)

5. Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка, причем h¢(x) ¹ 0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство

g(b)-g(a) h(b)-h(a) = g¢(c) h¢(c)

6. Доказательство. Применим теорему Ролля к функции

g(x)-g(a)-(h(x)-h(a))Q,

7. где

Q=(g(b)-g(a))/(h(b)-h(a))

8. Теорема. Лопиталя. Пусть функции g(x) и h(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x=a, т.е. g(a)=h(a)=0, тогда если существует предел отношения g¢(x)/h¢(x) при x® a, то существует и

lim x® a g(x)/h(x)

9. причем

lim x® a g¢(x)/h¢(x)= lim x® a g(x)/h(x).

4. Арифметические свойства дифференцируемых функций

Сумма f+g дифференцируемых функций f, g является дифференцируемой функцией, а ее производная равна (f+g)' = f' +g'

Произведение fg дифференцируемых функций f, g является дифференцируемой функцией, а ее производная равна (fg)' = f' g +f g'

Отношение f/g дифференцируемых функций f, g, при g не равной нулю, является дифференцируемой функцией, а ее производная равна (f/g)' = (f' g - f g' )/ g^2

 

 

5.Дифференцирование сложных функций

6.Обратная функция и ее дифференцирование. Производная функция y=acrsin

Если y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции g'(x)=1/f'(x).

Таким образом, производные взаимно обратных функций — обратные величины. Формула для производной обратной функции:

7 Таблица производных.

8.Дифференциал, его связь с приращением функции, геометрический смысл, свойства

)Дифференциа́л — линейная часть приращения функции. Дифференциал функции в точке может быть определён как линейная функция где f'(x₀) обозначает производную f в точке x₀.Таким образом df есть функция двух аргументов .Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция линейно зависящая от h и для которой верно следующее соотношение

Свойства дифференциала:

1. Постоянный множитель можно вынести за знак дифференциала:

2. дифференциал алгебраической суммы функций равен алгебраической сумме дифференциалов этих функций 3. дифференциал произведения 4. дифференциал дроби (дифференциал частного) 5. дифференциал сложной функции где d g(x), в свою очередь, можно дифференцировать дальше.

 

9..Инвариативность формы дифференциала сложной функции

Если Х является независимой переменной, то дифференциал функции y=f(x) можно записать так: dy=f / (x)dx. Покажем, что эта форма сохраняется и в случае, если x является не независимой переменной, а функцией. Действительно, пусть y=f(x) и x=ϕ(t), то есть y – сложная функция от t: y=f[ϕ(t)]. Тогда, dy=yt / dt. По правилу дифференцирования сложной функции: yt /=yx / ⋅ xt / . Отсюда, dy=yx / ⋅ xt / dt=yx / dx=f / (x)dx. Этим мы доказали следующее:

 

Теорема. Дифференциал сложной функции y=f(x), для которой x=ϕ(t), имеет такой же вид, dy=f / (x)dx, как и в том случае, когда аргумент x является независимой переменной. Это свойство называется – инвариантность формы дифференциала.

 

10.Производные высших порядков.

Если задана произвольная дифференцируемая функция y=f(x), тогда ее производная y /=f / (x) в свою очередь является функцией того же аргумента x. Поэтому, можно видимо искать производную и от этой функции. Производная от производной данной функции, если она существует, называется производной второго порядка, или второй производной от данной функции y //=f //(x), то есть (y / ) /=y //=f //(x). Здесь y /=f / (x) – производная первого порядка. Механический смысл: v=s /=f / (t); ω=v /=s //=f //(t) – это скорость изменения скорости движения, то есть ускорение. Можно ввести и дальнейшие производные: (y //) /=y ///, (y ///) /=y IV=f IV(x),… Определение. Производной (n+1)-го порядка от данной функции называется производная от производной n-го порядка этой функции (y n ) /=y n+1=f n+1(x

11.Дифференциалы высших порядков.

Дифференциалом -го порядка функции называется дифференциал от дифференциала -го порядка этой функции, то есть

 Известно, что для функции y=f(x) дифференциал dy=f / (x)dx, то есть он зависит от двух переменных: независимой переменной (или аргумента x) и dx=∆x; причем dx от x не зависит, так как приращение в данной точке x можно выбирать независимо от этой точки. Рассматривая dy=f / (x)dx только как функцию x, то есть, считая dx постоянным, можно найти дифференциал этой функции.

 Определение. Дифференциал от дифференциала данной функции y=f(x) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d 2 y или d 2 f(x), то есть по определению d 2 y=d(dy). d 2 y=d(dy)=d(f/ (x)dx)=[f/ (x)dx]/ dx=[f//(x)dx+f/ (x)⋅ 0]dx=f//(x)(dx)2 . Итак, d 2 y=f //(x)(dx)

 2 . Аналогично, можно определить дифференциалы второго, третьего и так далее порядков.

Определение. Дифференциалом n-го порядка (или n-ым дифференциалом) функции y=f(x) называется дифференциал от ее (n-1)-го дифференциала: d n y=d(d n-1y). Для функции y=f(x), аргумент которой является независимой переменной, справедливо равенство: d n y=f (n) (x)dxn . Отсюда, f (n) (x)= n n dx d y . Например, f / (x)= 3 3 /// 2 2 // ; ( ) ; ( ) dx d y f x dx d y f x dx dy = =

Определение. Производной n-го порядка данной функции (при условии, что ее аргумент является независимой переменной) называется отношение ее дифференциала n-го порядка к n-ой степени дифференциала независимой переменной. Мы знаем, что форма дифференциала первого порядка dy=f / (x)dx обладает свойством инвариантности. Однако форма дифференциала высшего порядка d n y=f n (x)dxn (n>1) не обладает этим свойством инвариантности. Поэтому, вообще говоря, производную f n (x) (n>1) в случае, когда x не является независимой переменной, нельзя рассматривать как отношение d n y к dxn .

Но условились сохранять запись f (n) (x)= n n dx d y , понимая n n dx d y не как отношение дифференциалов, а как новое символическое обозначение n-ой производной

12. НЕинвариативность формы дифференциала второго порядка

При , -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение зависит, вообще говоря, от того, рассматривается ли переменная как независимая, либо как некоторая промежуточная функция другого переменного, например, .

Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При n = 2 и :

• если — независимая переменная, то
• если и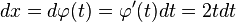

1.

2. при этом, и

С учётом зависимости , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.

13.Дифференцированность функций, заданных неявно

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

<< Пример 21.1

Найти производную функции у, заданную уравнением х³+у³-3ху=0.

Решение: Функция у задана неявно. Дифференцируем по х равенство х³+у³-3ху=0. Из полученного соотношения

3х²+3у²· у'-3(1· у+х· у')=0

следует, что у²у'-ху'=у-х², т. е. у'=(у-х²)/(у²-х).

 

14.Дифференцированность функций, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

 

15. Свойства функции непрерывной на замкнутом промежутке

 

 

16 ТЕОРЕМЫ

 

 

 

 

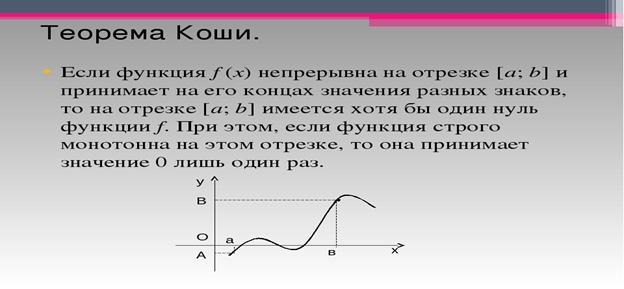
17.Теоремы о постоянстве, монотонности функции на интервале

 

 

18.Экстремум;необходимое и достаточное условие

Необходимое условие экстремума. Если точка является точкой экстремума функции то

или хотя бы одна из этих производных не существует.

Точки, для которых эти условия выполнены, называются стационарными или критическими. Точки экстремума всегда являются стационарными, но стационарная точка может и не быть точкой экстремума. Чтобы стационарная точка была точкой экстремума, должны выполняться достаточные условия экстремума.

Введем обозначения

Достаточное условие экстремума. Пусть функция имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку . Тогда:

1. если то точка является точкой экстремума для данной функции, причем будет точкой максимума при и точкой минимума при ;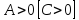

2. если то в точке экстремума нет;

3. если то экстремум может быть, а может и не быть.

---

Дата добавления: 2019-02-22; просмотров: 719; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!