Третье обоснование теории вероятностей
Если до Бореля было принято рассматривать либо вероятности конечного числа событий (типа бросаний монеты), либо непрерывные вероятности (типа попадания неточно измеренной величины в данный отрезок или квадрат), то Борель стал оперировать с бесконечными последовательностями цифр, т.е. со счетными множествами и, соответственно, со счетными вероятностями. При этом расплывчатое выражение "событие происходит с ничтожной вероятностью" уступило место точному термину "событие имеет нулевую вероятность", понимаемому так: событие возможно, но его вероятность выражается нулевой мерой. Пример из области непрерывных вероятностей: шар может упасть на плоскость любой своей точкой, однако вероятность того, что он упадет любой заданной точкой, равна нулю.
Вернемся к упомянутому примеру Бореля из области счетных вероятностей: равна нулю вероятность того, что наугад взятая последовательность цифр периодична. Вообще, нулевую меру имеет любая особенность в структуре действительного числа и, в частности, такая: если значение m-ой цифры зависит от значения n-ой (m>n). Этот фундаментальный факт значит, что почти всякое(*) иррациональное (а значит, и почти всякое действительное) число случайно по Ламберту.
Другое столь же фундаментальное свойство, которое следует из того, что все последовательности взяты по одному разу, звучит так: почти всякое вещественное (в том числе рациональное) число имеет столько же нулей, сколько и единиц (Борель назвал такие числа "нормальными"). Его можно выразить иначе: вероятность того, что в двоичной дроби число нулей равно числу единиц, равна единице. Легко видеть, что это утверждение есть ЗБЧ для идеальной монеты, брошенной бесконечное число раз [Кац, 1963, c. 26-36; Ширяев, 1998, c. 112–113]. Вместе оба свойства означают устойчивость частот.
|
|
|
Она тут не постулирована, а выведена из свойств поля вещественных чисел. Этот фундаментальный результат есть следствие реализационной симметрии множества действительных чисел, т.е. того факта, что каждая запись взята ровно один раз. Иначе говоря, Борель истолковал меру как вероятность, продолжив линию Кардано – Бернулли, когда вместо случайных испытаний производится математическое действие, "демонстрирующее все формы". Воттретье обоснование феномена вероятности. Исторически оно явилось первым.
Борель фактически ответил на вопрос Ламберта: отсутствие "порядка сходства" между знаками иррационального числа есть наиболее общая симметрия, какая вообще мыслима среди чисел. Любая зависимость между знаками числа, даже самая на вид симметричная, являла бы собой более частную симметрию. Однако этот ответ чисто формален и практически бесполезен, пока не сказано, как устроено множество тех конкретных чисел, с которыми мы обычно имеем дело. А вдруг большинство интересных нам чисел как раз неслучайны по Ламберту? Ответ будет дан в п. 8.
|
|
|
Тройная симметрия
Симметрийный подход многое разъясняет и в отношении предельных теорем. Центральная предельнаятеорема (ЦПТ), рассмотренная в главе 3, гласит, что сумма независимых случайных величин (одинаковых или различных) в широких условиях сходится к одному-единственному распределению (гауссову). Точную формулировку см. например [Феллер, 1984, с. 301], нам же достаточно следующего: суммирование случайностей приводит к гауссову распределению, если выполнены три условия:
1) равновозможность (самих событий и их серий);
2) аддитивность (результирующая случайность есть сумма);
3) одномасштабность (дисперсии слагаемых равномерно ограниченны).
Вся тройка в целом достаточна для выполнения ЦПТ. Этой тройке условий ранее [Чайковский, 1988; 1990] было дано название тройная симметрия. Тройка достаточно разнородна – равновозможности событий можно придать точный симметрийный смысл, введя понятия микро- и макросостояний; равновозможности серий (независимости событий) можно придать точный смысл, введя новую форму симметрии – реализационную; аддитивности тоже можно придать точный смысл, но она существенна не сама по себе, а как единственный обследованный в ТВ пример действия, обладающего симметрией в форме коммутативности и ассоциативности – сложение им обладает:
|
|
|
a + b = b + a; (a + b) + c = a + (b + c);
что же касается одномасштабности, то она является симметрией лишь в некотором фигуральном смысле.
Столь же различна и их роль в отношении необходимости – одномасштабность для выполнения ЦПТ, грубо говоря, необходима (точнее см. ниже), тогда как аддитивность – не более чем один обследованный пример. Что касается равновозможности событий, то она (точнее, равновозможность микросостояний), по-видимому, необходима; наоборот, независимость (равновозможность серий) может нарушаться, но – в определенных пределах, о которых еще будет речь.
Предоставляя математикам принять (уточнив смысл) или отвергнуть высказанные положения, ограничусь несколькими соображениями, которые призваны прояснить суть тройной симметрии и облегчить переход к случайностям, ее не имеющим.
1. Рассмотренные в главе 3 примеры действия ЦПТ показывают, насколько важна обычная наглядная симметрия: равномерная плотность симметрична, и ЦПТ весьма эффективна – сумму уже трех слагаемых можно заменить нормальной плотностью; наоборот, плотность хи-квадрат радикально асимметрична, и сходимость чисто номинальна. В промежуточных случаях, когда асимметрия не столь радикальна (диссимметрия) эффективность ЦПТ тоже промежуточна: таковы пуассоново, логнормальное и другие скошенные и смещенные колоколообразные плотности.
|
|
|
2. Читая учебник Уиттла, довольно легко понять, что тройная симметрия перемалывает любую совокупность случайностей, ею обладающую, в одну – гауссову, самую симметричную. Можно пойти и дальше: признать, что всякая устойчивость частот есть разновидность симметрии [Марков В.А., 1988, c. 50].
3. Просчет Мизеса состоял в отказе от симметрийного подхода. Постулировав беспорядочность, он отверг симметрию, ибо полагал эти идеи противоположными. По-моему же, они взаимодополнительны (в том смысле, какой придавал этому термину Нильс Бор – см. п. 5-7): симметрийное понимание вероятности (как инварианта структуры равновозможностей) взаимодополнительно к пониманию вероятности как предела частоты. Подробнее см. конец главы 5.
4. И само нормальное распределение, и его двухсотлетний успех выглядят загадочно. Как признал сто лет назад Пуанкаре [1999, c. 140], нормальное распределение не имеет строгого вывода, а сделанные самим Гауссом при его выводе допущения не только грубы, но и прямо нарушаются. Тем не менее "все верят в этот закон. Как мне однажды сказал П. Липпманн, потому что экспериментаторы думают, что это математическое утверждение, а математики – что это результат эксперимента". Яркость афоризма за сто лет не потускнела, но загадочность закона несколько поубавилась – чем менее симметрична ситуация, тем хуже он действует. Слова "менее симметричная ситуация" означают уменьшение роли составляющих тройной симметрии в исследуемом случайном явлении. Поясню этот тезис примерами.
5. Самые легкие примеры касаются условия равномерной ограниченности дисперсии случайных слагаемых, поскольку оно, грубо говоря, необходимо (точнее см. [Феллер, 1984, c. 299, 301; Стоянов, 1999, c. 180], где показано, что "условие Линдеберга", ограничивающее дисперсию случайной величины и обычно называемое необходимым и достаточным, не всегда является необходимым). Даже у распределения с плотностью f(x), для которого сама ЦПТ грубым образом не выполняется, может иметься какая-то характеристика g(x), сходящаяся к нормальному распределению, если и f, и g симметричны. Таково распределение Коши
F(x) = 1/2 + (1/p) arctg x,
имеющее плотность: F'(x) = f(x) = 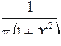 ,
,
у которого ЦПТ выполнена для медианы, т.е. для х, задаваемого уравнением F(x)=1/2. Очевидно, что у распределения с симметричной плотностью медиана совпадает со средним значением плотности, а это и есть та величина, которую обычно хотят найти.
Плотность Коши имеет, как и гауссоида, колоколообразную форму, однако убывает с ростом х так медленно, что бесконечны не только дисперсия, но и мат. ожидание. Распределение Коши естественным образом возникает в астрономических расчетах, поскольку ему подчиняется случайная величина x=tg h, где угол h распределен равномерно между -p/2 и +p/2. Тем самым, на границах области определения величины h переменная х неограниченна. Ввиду бесконечности мат. ожидания тут среднее от любого числа измерений величины х оказывается не точнее, чем единичное измерение. Это значит, что грубо нарушен даже ЗБЧ, не говоря уж о ЦПТ. Вроде бы статистика бессильна, но спасает симметрия распределения: зная, что случайная величина Х распределена по Коши, нужно не суммировать сами х, а вычислять F(x) для каждого х по формуле, определяющей функцию распределения:
F(x) = P(y<x),
где y – измеряемые величины (в данном случае тангенсы), а затем решить уравнение F(x) = 1/2 и тем самым вычислить выборочную медиану для данного х. Нормированная сумма выборочных медиан для различных случайных значений х, распределенных по Коши, сходится к нормальному распределению [Варден, 1960, c. 107].
6. В качестве примера нарушения условия аддитивности в главе 3 приведено распределение хи-квадрат: если складывать не сами случайные величины, а их квадраты, то ЦПТ хоть и плохо, но выполняется (рис. 3). Другой пример: случайные величины, распределенные нормально, можно перемножать, т.е. складывать их логарифмы – получится логнормальное распределение, для которого ЦПТ тоже справедлива. Это – единственный известный мне пример, когда тройная симметрия достигается за счет не сложения, а другого симметричного действия над случайными величинами (умножения – оно тоже обладает коммутативностью и ассоциативностью).
7. Наоборот, ЦПТ может нарушаться даже для очень "хороших" распределений, если только равномерная ограниченность слагаемых нарушена достаточно сильно. Самый для меня удивительный пример (из простых) – сумма равномерно распределенных величин, определенных на различных интервалах. Казалось бы, пример на рис. 2 должен быть достаточно устойчив к вариациям, однако стоит достаточно быстро устремить длину n-го интервала к нулю (т.е. случайные величины – к детерминированному пределу), и сходимость суммы n слагаемых к нормальному распределению исчезает [Феллер, 1984, c. 303]. Здесь оказывается слишком велика роль первых слагаемых по сравнению с последующими.
Противоположный случай (когда длины интервалов растут – приведен там же) менее удивителен. Вся его удивительность состотит в том, насколько быстро должна расти длина n-го интервала (как 2N), чтобы ЦПТ перестала выполняться. Это говорит о большом запасе ее прочности.
Другой пример, когда экспоненциальное расширение области определения случайной величины разрушает саму стохастичность, мы рассмотрим а п. 7-1.
Дата добавления: 2019-02-22; просмотров: 218; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
