Суммирование случайных величин
Очень многие виды случайностей, если суммировать их в большом количестве, образуют итоговую случайную величину с одной и той же плотностью распределения – гауссоидой. Поэтому гауссоида оказывается наиболее важной плотностью распределения, отчего само гауссово распределение получило имя нормального.
Сто лет назад французский математик Анри Пуанкаре [1999, гл. 10–11] подробно исследовал феномен гауссовости и пришел к выводу, что его широкая распространенность – итог объективного существования в природе суммирования малых величин. Это объяснение негласно царит до сих пор.
Для читателей, далеких от ТВ, поясню смысл суммирования независимых случайных величин, поскольку это важно для понимания дальнейшего. Вероятность совместного осуществления пары исходов независимых испытаний по определению равна произведению вероятностей этих исходов; эти произведения надо, для получения функции распределения суммы двух независимых случайных величин, сложить, а если величины непрерывны, проинтегрировать. Плотность распределения суммы, получаемая интегрированием произведения плотностей двух складываемых случайных величин, называется свёрткой. Для получения плотности распределения трех независимых случайных величин надо произведение свертки (двух величин) на плотность третьей величины снова проинтегрировать, т.е. получить свертку свертки. При этом порядок суммирования (какую величину считать третьей) не имеет значения. То есть для изучения суммы n+1 независимых непрерывных случайных величин надо получить n-кратную свертку. Формулы можно найти в разных учебниках, из которых рекомендую [Шметтерер, 1976, c. 85; Тутубалин, 1992, с. 89].
|
|
|
Смысл ЦПТ удобно пояснить двумя примерами. На рис. 2 показано, как гауссоида образуется из совсем не похожих на нее прямоугольников. Если случайная величина X1 распределена равномерно на интервале –1<х<1, то плотность ее распределения изобразится отрезком y=1/2 (график всякой плотности распределения содержит под собой фигуру единичной площади). Если случайная величина X2 распределена точно так же, причем принимает отличные от нуля значения на интервале –1<х<1 независимо от X1, то их сумма распределена согласно треугольной плотности: пределы возможных изменений расширятся (–2<х<2), а центральные значения окажутся более вероятными. Аналогично, сумма трех таких величин обладает гладкой плотностью y(x), образованной отрезками парабол, причем область изменения суммы снова расширилась: –3<х<3. Вот почему мы ограничиваемся на практике тремя измерениями (простаферезис Лейбница – см. гл. 2): в большинстве реальных процедур измерений среднее по первой тройке измерений дает основную информацию об измеряемой величине; усреднение больше чем по трем точкам полезно лишь для тех редких случаев, когда хотя бы одно из первых трех слагаемых дало сильное отклонение от истины. Заодно здесь виден и ответ на вопрос Симпсона.
|
|
|
Вот почему мы пользуемся одними и теми же приемами (например, оценкой Муавра, т.е. 
) всюду, где видим многократную однотипную случайность. Как видим, ТВ вполне подтвердила ту "природную математику", о которой писал Лейбниц.
Однако подтверждение это может быть иллюзорным. Пример, изображенный на рис. 3, показывает, что безоглядно верить в ЦПТ не следует. Здесь суммируются величины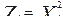 
, где Xi – одинаковые независимо распределенные нормальные случайные величины. 
– хорошо известное в статистике распределение "хи-квадрат". Казалось бы, здесь сходимость к гауссоиде должна быть лучше, чем на рис. 2, но выходит не так.
Рассмотрим случайную величину Z, значения которой z являются квадратами величин х. Если случайная величина X принимает любые числовые значения, то Z – только неотрицательные, поэтому ее плотность g(z) имеет максимум при z=0 и монотонно убывает с ростом z (как говорят, является однохвостой). Чтобы найти g(x), надо вспомнить, что реальный вероятностный смысл имеет функция распределения, тогда как плотность распределения (ее производная) – скорее иллюстративный.
|
|
|
Функция распределения G(z) случайной величины Z есть вероятность того, что
x2 < z. Имеем: если x2 < z, то 
, а потому
.
Введя переменную z = x2, получим:
,
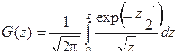где функция под знаком интеграла как раз и есть функция g(z).
Удивительно и, пожалуй, контр-интуитивно то, что g(z) при z=0 обращается в бесконечность. Однако при суммировании даже двух таких случайных величин получаем ограниченную плотность, а плотности всех последующих сумм обращаются при z=0 в нуль, что тоже неожиданно.
Плотности величин Zi на рис. 3 резко асимметричны ("однохвосты") за счет того, что отрицательные значения аргументов x случайных величин Xi отображаются в положительные значения аргументов z величин Zi. Поэтому симметрия суммы складывается медленно и нечетко, приближение ее к гауссоиде достигается путем расползания самой этой гауссоиды и смещением ее вершины вправо [Варден, 1960, с. 118; Шметтерер, 1976, с. 93]. Хотя формально ЦПТ и тут верна, пользоваться ею практически нет возможности.
Поскольку сама по себе сумма Sn случайных величин с ростом n стремится, как правило, к бесконечности, вместо нее в ЦПТ рассматривается нормированная сумма
|
|
|
sn = (Sn — M(Sn))/D(Sn),
где M(Sn) – математическое ожидание суммы Sn, а D(Sn) – ее дисперсия.
В нынешней формулировке ЦПТ – очень сильная теорема. В частности, в ней не требуется, чтобы случайные величины были распределены одинаково. Она в форме, какую придал ей финский математик Ярл Линдеберг (1922 г.), звучит так: нормированная сумма взаимно независимых случайных величин имеет распределение, сходящееся к нормальному, если дисперсии слагаемых равномерно ограничены (т.е. не превосходят некоторого общего для всех слагаемых числа D0).
Независимость величин не является необходимой – существуют различные виды зависимости слагаемых, не нарушающие ЦПТ (см. например, работы, указанные у Феллера [1984, c. 304], и гл. 7 книги [Ширяев, 1989]). Наоборот, ограниченность дисперсий необходима [Феллер, 1984, c. 301]. Мы вернемся к этому в главе 4.
Изменился и ЗБЧ: он выражается теперь формулами типа (1) и мало похож на ту теорему, что доказал Я. Бернулли. Индивидуальное испытание исчезло: вместо него исследуется распределение вероятностей случайной величины. Само существование вероятности этим постулируется, так что прежний смысл (существование предела, к которому стремится частота в длинной серии испытаний) утрачен, и встает вопрос: в чем же теперь смысл ЗБЧ? Только в выяснении условий сходимости? А разве возможна вероятность, к которой частота не сходится? (Этим вопросом мы займемся в гл. 4.) В частности, выяснено, что для сходимости частоты к вероятности достаточно, чтобы дисперсия этой частоты существовала, т.е. не обращалась в бесконечность при бесконечном числе испытаний.
Это условие не является необходимым – существуют более слабые требования, например, в теореме Хинчина. Она гласит: если независимые случайные величины распределены одинаково, то их нормированная сумма сходится к пределу (математическому ожиданию) даже если их дисперсии бесконечны [Тутубалин, 1992, c. 100; Стоянов, 1999, c. 152]. (ЗБЧ в форме сходимости частоты к вероятности и в форме сходимости суммы к мат. ожиданию равносильны.) Теорему Хинчина мы рассмотрим в главе 7.
ЗБЧ – более широкое утверждение, чем ЦПТ: есть много случайных величин, у которых частоты сходятся к вероятностям, но суммы этих величин к нормальному распределению не сходятся. Дело, как легко понять, в том, что для дисперсий при этом не существует единого числа D0. Точнее см. [Феллер, 1964, с. 260]. Это важно помнить, чтобы не применять (как часто делают) ЦПТ ко всем стохастическим случайностям.
Дата добавления: 2019-02-22; просмотров: 658; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!