Независимость без случайности
Почему же все комментаторы дружно видят в теореме Бернулли независимые испытания, которых там нет? Дело в том, что идея независимости лежит в основе нынешней ТВ, фактически заменяя в ней отсутствующую идею случайности. Как писал в 1933 г. Колмогоров, без понятия независимости ТВ осталась бы просто частью теории меры и не могла бы "доставить никакого базиса для развития большой оригинальной теории". Независимость он ввел просто – отказавшись обсуждать философский смысл явления(*) , он дал определение: испытания называются независимыми, если вероятность их совместного наступления равна произведению вероятностей этих испытаний [Колмогоров, 1998, c. 10–12].
Если так, то у Бернулли надо было найти только одно – подходящие произведения. И они, естественно, нашлись. Его теорема доказана не для случайных бросаний, а для методичных раскладок, но если разделить обе части равенства (2) на tN, то получится очевидное равенство: сумма вероятностей всех возможных раскладок равна 1, если положить, что каждое произведение вида
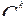rN—ksk
есть вероятность раскладки, в которой k костей легло на незакрашенные грани, а (N–k) – на закрашенные. Если же вероятность совместного наступления событий выражается через произведение этих событий, то события, как мы видели, называются независимыми.
(Замечание для математиков: правило перемножения вероятностей свидетельствует вовсе не о физической (или, шире, онтологической) независимости событий, а о выполнении некоторого свойства ортогональности для множества функций, именуемых случайными величинами. Об этом мимоходом писал Алимов [1980, c. 32]: "С математической стороны, теорема Бернулли и другие формы ЗБЧ... представляют собой не что иное, как теоремы об ортогональных функциях". Данным свойством, в частности, обладает полное множество раскладок, не содержащее никакой случайности, и это совпадение позволило видеть в чисто комбинаторной теореме Бернулли первый вариант ЗБЧ.)
|
|
|
Итак, независимость испытаний – лишь одна из интерпретаций "золотой теоремы", случайностная интерпретация неслучайной процедуры. "Мы на самом деле не знаем, что такое независимость, но чем бы она ни была, если она имеет смысл, она должна обладать следующими свойствами" – записали двое методологов и тут же повторили колмогоровское определение независимости [Кац, Улам, 1971, c. 72]. Это верно, но следовало бы добавить: отнюдь не всякая совокупность событий, обладающая этим свойством, являет независимость в обычном понимании. То есть налицо достаточность, а необходимости нет. Мы вернемся к этому вопросу в главе 6, когда пойдет речь о роли независимости в теории динамического хаоса.
|
|
|
Я уже приводил фразу: "И что не дано вывести a priori, то, по крайней мере, можно вывести a posteriori, т.е. из многократного наблюдения". Оптимизм Бернулли странен с нашей нынешней позиции (вероятность по выборке не восстанавливается, ибо частота к вероятности не сходится – на этом обжегся Мизес). Но оптимизм вполне естествен с позиции реализации "всех форм" Кардано: если та "многогранная кость", о которой мы выше вели речь, действительно существует, то рано или поздно конкретное число "раскладок" укажет на нее с любой наперед заданной точностью; и, что не менее важно, дальнейшее удлинение раскладок не отклонится от ранее найденного r/s (чего не скажешь о частотах при реальных бросаниях).
Поэтому и саму "золотую теорему" можно условно назвать теоремой Кардано – Бернулли . Случайность в ней не столько описана, сколько обойдена, отчего и возникла потребность в интерпретациях, спор о которых не затих до сих пор. Это важно помнить потому, что общепринятая схема Колмогорова развила именно схему Бернулли, которая, как видим, была чисто детерминистической.
Точнее, у Бернулли бином Ньютона являл собою всего лишь форму записи всех подмножеств множества элементарных событий. В системе понятий, где число событий несчетно, аналогичное множество строится сложнее (но в принципе так же) и именуется борелевским полем событий, или сигма-алгеброй. В схеме Бореля – Колмогорова, как и у Бернулли, каждое элементарное событие взято ровно один раз т.е. случайность вновь не столько описана, сколько обойдена. Обеим вероятностям (Р и р) в формуле (1) теперь приписан один и тот же статус – обе понимаются как меры. Эту унификацию математики восприняли как успех в понимании вероятности, хотя, на мой взгляд, его тут не было, а была лишь спутана частота со степенью уверенности.
|
|
|
Дата добавления: 2019-02-22; просмотров: 297; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!