Характер господарських ситуацій, які передбачають використання математичного програмування, теорій ігор та теорій масового обслуговування

Одним із найбільш ефективних, фундаментально досліджених і експериментально перевірених на практиці економіко-математичних моделей є клас оптимізаційних задач з лінійною формулою взаємозв’язків, математичним апаратом якого є лінійне програ­мування.

До основних вимог, які слід враховувати при застосуванні методів лінійного програмування, належать такі: будь-яка задача повинна бути представлена в математичній формулі з допомогою системи нерівностей або рівнянь; будь-який одержаний розв’язок не повинен вступати в протиріччя з економічним змістом задачі; система лінійних рівнянь повинна бути визначеною; для знаходження оптимального розв’язку системи необхідно сформулювати критерій оптимальності і визначити його у формі цільової функції, яка в процесі розв’язку одержить екстремальне значення.

Розглянемо модель оптимізації виробничої програми підприємства, зміст якої полягає в наступному. Для організації виробництва деяких видів продукції підприємство має в наявності ряд виробничих ресурсів, по яких задано обсяги і норми їх використання на одиницю продукції.

Відомий розмір попиту на окремі види продукції, а також ефе­ктивність їх виробництва (ціна або прибуток за одиницю продукції, собівартість одиниці продукції). Необхідно визначити: оптимальну виробничу програму підприємства по випуску різних видів продукції на основі наявних ресурсів.

Для побудови економіко-математичної моделі задачі введемо такі позначення: і – індекс виду ресурсу, і = 1, 2, ..., n; j – індекс виду продукції,
j = 1, 2, ..., m; а_ij – норма використання і-го виду ресурсу на одиницю j-го виду продукції; А_і – обсяг запасів і-го виду ресурсу; В_j – величина договірних поставок j-го виду продукції; С_j – ефективність (ціна або прибуток) ви­робництва одиниці продукції j-го виду; х_j – обсяг виробництва j-го виду продукції; J – множина видів продукції. Враховуючи введені позначення, математична модель набуде виду.

Знайти розв’язок {x _j ³ 0, j = 1, ..., m}, який забезпечить

         max

при умовах:

1) по використанню наявних ресурсів:

, і = 1, 2, ..., n;

2) по виконанню договірних поставок

x_j ³ В_j, j Î J.

Для одержання числових розв’язків задач лінійного програмування можна використовувати існуючі пакети прикладних програм.

Методи динамічного програмування застосовуються в розв’язку оптимізаційних задач, в яких цільова функція або обмеження, чи пер­ше і друге одночасно характеризуються нелінійними залежностями. Ознаками нелінійності є наявність змінних у степені, під коренем, під знаком логарифма.

У практичній діяльності нерідко доводиться приймати рішення в конфліктних ситуаціях. Це пов’язано з практичною важливістю, яку відіграють конфлікти в житті і ро­звитку суспільства і з специфічною складністю конфлікту як явища, в якому доводиться приймати рішення. Справа в тому, що в умовах конфлікту особі, що приймає рішення необхідно раху­ватись не тільки із власними цілями, а також з цілями, що ставить пе­ред собою інша особа. Необхідно враховувати також, крім об’єктивних, відомих йому причин конфлікту, ще й ті рішення, які може прийняти партнер, і які, взагалі кажучи, йому не відомі. Звідси випливає, що математичні моделі, які враховують конфлікти, є складними і специфіч­ними.

Теорія ігор є теорією математичних моделей, в яких учасники мають різні інтереси, і для досягнення своїх цілей користуються різними шляхами. Основними поняттями теорії ігор є поняття конфлікту, кроку, стратегії. Конфліктом називають всяке явище, про яке доцільно з’ясувати: хто і як бере в ньому участь, які можливі його наслідки, хто є зацікавленим у тих наслідках, у чому ця зацікавленість проявляється і т.п. Всі ці дані повинні бути записані у вигляді най­простіших математичних співвідношень. Учасники, які беруть участь у конфлікті, будуть називатися гравцями. В грі можуть переплітатися інтереси двох чи більше гравців. У першому випадку гра називається парною, в другому – множинною. Під грою розуміють таку послідовність дій (ходів) гравців (їх, як правило, позначають терами А, В, С...), яка здійснюється у відповідності до чітко сформульованих правил, які враховують всі можливі ситуації, що можуть трапитись. Вважають, що інтереси гравців піддаються кількісному опису, тобто задаються певними числами. Ходом гравця називають вибір однієї з можливих, згідно правил гри, дії та її здійснення. Стратегією гравця називають план, що показує, який вибір він буде здійснювати в будь-якій можливій ситуації і при будь-якій можливій фактичній інформації.

Завданням теорії ігор є розробка рекомендацій гравцям, тобто визначення для них оптимальних стратегій. Під оптимальною страте­гією розуміють таку стратегію, яка при багатократному повторенні за­безпечує гравцю максимально можливий середній виграш. Очевидно, для кожної гри може бути своє поняття оптимальності. Для одного класу гри одні принципи оптимальності, для другого – зовсім інші, причому, можливо, навіть протилежні.

Конкретні класи теорії ігор одержують, накладаючи на компоненти гри різні обмеження. В залежності від цілей гри і її характеру допус­кається така умовна класифікація:

Ø  за кількістю гравців, які беруть участь у грі:

а) гра двох осіб;

б) гра трьох осіб і т.д.;

Ø  за кількістю стратегій:

а) задачі із скінченою кількістю стратегій;

б) задачі з нескінченною кількістю стратегій;

Ø  за властивостями цільової функції гри:

а) ігри з нульовою сумою;

б) ігри з ненульовою сумою;

Ø  за попередньою домовленістю відносно можливихдій:

а) кооперативні (з деякими домовленостями);

б) некооперативні (без будь-яких домовленостей) і т.д.

Розглянемо гру, в якій приймає участь два гравці, один з яких може вибрати стратегію і із n своїх можливих стратегій (і = 1, 2, …, n), а другий, не знаючи вибору першого, вибирає стратегію із своїх можливих стратегій (j = 1, 2, …, m). В результаті, перший гравець (А) виграє a_ij, а другий (В) програє цю величину.

Величини a_ij утворюють платіжну матрицю (матрицю гри):

 

		B1	…	Bm
	A1	a11	…	a1m
[аij] =	A2	a21	…	a2m
	…	…		…
	An	an1	…	anm

 

Рядки матриці [а_ij] відповідають стратегіям (A₁, A₂, …, А_n) гравця A, а стовпці – стратегіям (B₁, B₂, …, B_m) – B. Дані стра­тегії називаються чистими. Будемо вважати, що при а_ij > 0 гравець А виграє, а гравець В програє величинуа_ij. Якщоа_ij < 0,то, навпаки, виграє гравець В і програє гравець А.

Спочатку знайдемо найкращу із стратегій гравця А, тобто най­кращу серед А₁, А₂, …, А_n, з врахуванням можливих відповідей на неї гравця В. При цьому ми повинні розраховувати на те, що на довільну стратегію А_і гравець В відповість стратегією В_j, для якої виграш гравця А виявиться мінімальним. Для знаходження стратегіїВ_j необхідно в і-му рядку платіжної матриці знайти б_і = min а_ij. При зміні стратегій гравця А одночасно будуть мінятись відповідні їм чис­ла б_і. Зрозуміло, що гравцеві А вигідно завжди зупинитися на такій стратегіїА_і, для якої значенняб= max б_і, або, вра­ховуючи значення б_і, одержимоб = max min а_ij.

 Числоб називається нижньою ціною гри або максиміном, а відповідна його стратегія (рядок) – максиміною.

Якщо гравець А буде дотримуватись максиміної стратегії, то йому, при довільній поведінці гравця В, в будь-якому випадку гарантований виграш не менший б.

Аналогічно можна визначити найкращу стратегію для гравця В, мета якого привести виграш гравця А до мінімуму. Для цього гравець В прагне для кожної своєї стратегіїВ_j одержати максимальне значення виграшу при довільній стратегії гравця, тобто він шукає зна­чення в_j = max а_ij.

Проте гравець В не може розраховувати на те, що гравець А дозволить йому одержати будь-який з виграшів b_j. Єдине, на що може розраховувати гравець В, то це на те, щоб одержати виграш, який буде не меншим за величину b = min max а_ij. Величина b називається верхньою ціною гри або мінімаксом, а відповідна йому стра­тегія гравця (стовпець) – мінімаксною. Мінімаксна стратегія є найбільш обережною стратегією для гравця В, яка забезпечує йому в будь-якому випадку програш не більший b і, відповідно, виграш гравцеві А, так само не більший b. Якщо б = b = v, то число v на­зивається ціною гри.

Гра, для якоїб = b, тобто мінімаксне значення рівне максиміному називається грою із сідловою точкою. Для гри із сідловою точкою знаходження розв’язку полягає у виборі максиміної і мінімаксної стра­тегій, які являються оптимальними. «Оптимальність» тут означає, що ні один гравець не прагне змінити свою стратегію, оскільки його суперник може на це відповісти вибором іншої стратегії, яка може дати гірший результат для першого гравця. Взагалі значення гри повинно задовольнити нерівності:

[Максиміне значення] ≤ [Значення гри] ≤ [Мінімаксне значення]

 Покажемо застосування теорії ігор у формуванні виробничої програми пивзаводу. Для прикладу візьмемо такі умовні дані: витрати пивзаводу на один декалітр бочкового пива складають 4 грн., пляш­кового – 4,5 грн. Ціна реалізації бочкового пива 8 грн., пляшкового – 8,5 грн. За даними спостережень за минулі роки, завод може реалізувати упродовж літніх місяців в умовах теплої погоди 4 млн. дкл бочкового пива і 2 млн. дкл пляшкового, а при холодній погоді – 2 млн. дкл боч­кового і 3 млн. дкл пляшкового. Необхідно сформувати виробничу програму підприємства так, щоб воно завжди отримувало середній прибуток, незважаючи на погодні умови.

 Пивзавод у цій ситуації може використовувати дві стратегії: стратегія А – в розрахунку на теплу погоду; стратегія В – в розрахун­ку на холодну погоду. Природа теж може вибирати дві стратегії: С – стратегія теплого літа; D – прохолодного.

Якщо пивзавод прийме стратегію А, то пиво, що відповідає теплій погоді (стратегія природи С), буде повністю реалізоване, при­буток заводу складе: 4 млн. дкл (8 – 4) + 2 млн. дкл (8,5 – 4,5) = 24 млн. грн.

Якщо завод буде здійснювати свою стратегію А в умовах прохолодної погоди (стратегія природи D), то пляшкове пиво буде реалізоване пов­ністю, а бочкове – лише у кількості 2 млн. дкл. Прибуток у цій ситуації складе:

2 млн. дкл (8 – 4) + 2 млн. дкл (8,5 – 4,5) – 2 4,0 = 8 млн. грн.

Аналогічно визначаємо прибуток заводу у випадку використання ним стратегії В. Тобто, завод візьме стратегію на холодну погоду, а погода виявиться теплою. В цьому випадку бочкове пиво буде реалізоване пов­ністю, а пляшкове в кількості 2 млн. дкл. Прибуток підприємства в цьому випадку складе: 2 (8 – 4) + 2 (8,5 – 4,5) – (3 – 2) 4,5 = 11,5 млн. грн.

Використання цієї ж стратегії в умовах холодної погоди приведе до інших результатів: 2 (8 – 4) + 3 (8,5 – 4,5) = 20 млн. грн.

Розглядаючи завод (Р₁) і природу (Р₂) як двох гравців, отримаємо так звану платіжну матрицю вигляду:

                                      Платіжна матриця                       (млн. грн.)

Гравці	Р2 (природа)
Р1 (підприємство)	Стратегія	Стратегія С	Стратегія D	Мінімальне по рядках
	Стратегія А	24	8	8
	Стратегія В	11,5	20	11,5
	Максимальне по стовпцях	24	20

 

Із платіжної матриці видно, що гравець Р₁ (підприємство) ніколи не отримає прибуток, менший 8 млн. грн. Якщо погодні умови співпадуть з вибраною стратегією, то прибуток підприємства буде складати 24 або
20 млн. грн. Якщо гравець Р₁ буде постійно використовувати стратегію А, а гравець Р₂ – стратегію D, то виграш знизиться до 8 млн. грн. Невисоким буде прибуток, якщо гравець Р₁ буде постійно використовувати стратегію В, а гравець Р₂ – стратегію С. Звідси висновок, що найбільший прибуток підприємство забезпечить собі тоді, коли буде поперемінно використовувати то стратегію А, то стратегію В. Така стратегія називається змішаною, а її елементи А і В – чистими стратегіями.

Якщо гравець Р₁ прийме оптимальну змішану стратегію, то, незалежно від стратегії гравця Р₂, він повинен отримати однаковий середній прибуток.

 Позначимо частоту використання гравцем Р₁ стратегії А через f, тоді частота використання ним стратегії В буде рівна 1 – f. Розрахуємо середній прибуток за формулою середньоарифметичної зваженої:

 24^.f  + 11,5 (1 – f ) = 8 f  + 20^. (1 – f );

 24,5f  =  8,5;

; .

 Дійсно, при стратегії С гравця Р₂ середній прибуток підприємства складе:

 млн. грн.

 При стратегії D гравця Р₂ середній прибуток підприємства складе:

 млн. грн.

 Значить, гравець Р₁, використовуючи чисті стратегії А і В у співвідношенні 17:32, буде мати оптимальну змішану стратегію, що забезпечить йому в будь-якому випадку середній прибуток у сумі 15,8 млн. грн. Нарешті, визначимо кількість бочкового і пляшкового пива, які повинен виготовляти завод для оптимізації свого прибутку:

(4 млн. дкл бочк. + 2 млн. дкл пляшк.)  + (2 млн. дкл бочк. +
+ 3 млн. дкл пляшк.) [17(4 млн. дкл бочк. + 2 млн. дкл пляшк.) +
+ 32 (2 млн. дкл бочк. + 3 млн. дкл пляшк.)] = [68 млн. дкл бочк. +
+ 34 млн. дкл пляшк. +  64 млн. дкл бочк. + 96 млн. дкл пляшк.] =
 = =  2,69 млн. дкл бочк. + 2,65 млн. дкл пляшк.

Отже, оптимальна стратегія заводу означає випуск 2,69 млн. дкл бочкового пива і 2,65 млн. дкл пляшкового. Тоді при будь-якій погоді він отримає середній прибуток у сумі 15,8 млн. грн.

Завданням теорії масового обслуговування є аналіз та дослідження явищ і процесів, що виникають у системах масового обслуговування (СМО). Одним з головних завдань теорії є визначення таких характер­них ознак системи, які забезпечують задану якість її ефективного функціонування, мінімальний час очікування, мінімальну середню до­вжину черги тощо.

Довільна СМО складається із вхідного потоку, черги, апаратів (каналів) обслуговування та вихідного потоку. Наприклад, надходження заявок на ремонт устаткування – вхідний потік; очікування ремонту – черга; ремонтні бригади – апарати обслуговування; відремонтоване устаткування – вихідний потік.

Економічна ефективність СМО буде залежати від вхідного по­току, кількості каналів обслуговування та організації системи обслуго­вування. Так, будівельна організація в своєму розпорядженні має 5екскаваторів та 15 автомашин для транспортування землі. У даному випадку маємо декілька варіантів вивезення землі із будівельних об’єктів. Можна всі екскаватори зосередити на одному об’єкті, тоді ефективно будуть використовуватися транспортні засоби, але буде втрачатися час на переїзд екскаваторів від одного об’єкта до іншого. Якщо наявний парк екскаваторів рівномірно розподілити між будівельними об’єктами, тоді екскаватори будуть простоювати в очікуванні транспортних засобів. Отже, в кожному окремому випадку необхідно вибирати ту або іншу форму організації обслуговування.

Дуже часто як критерій ефективності використовується мінімізація витрат пов’язаних з очікуванням вимог у черзі та простою каналів обслугову­вання.

Припустимо, що в систему входить 5 каналів обслуговування. Позначимо: М₁ – середнє число вимог у черзі; М₂ – середнє число вільних каналів обслуговування;С₁ – вартість очікування однієї вимо­ги за одиницю часу; С₂ – вартість простою одного апарата за одиницю часу. Враховуючи введені позначення, повна вартість витрат, пов’язаних з очікуванням та простоєм за інтервал часу Т, буде мати вигляд:

F(S) = (C₁M₁ + C₂M₂) T – min.

Довільна СМО має свою відповідну організаційну структуру. За своєю структурою вона може бути одно- або багатоканальною. Наприклад, у цеху певний вид устаткування обслуговує одна брига­да – система одноканальна; те ж саме, тільки три бригади – система ба­гатоканальна.

Іншою класифікаційною ознакою є час перебування вимог у системі до початку обслуговування. На основі даної ознаки всі системи можна поділити на три групи: системи з необмеженим часом очікування, системи з відмовою (втратами) та системи змішаного типу.

У системі з відмовою будь-яка вимога, заставши всі канали зайня­тими, покидає її. У системах з необмеженим часом очікування вимога, заставши всі канали зайнятими, вимушена очікувати черги до тих пір, поки один з них не звільниться. Системи змішаного типу характе­ризуються тим, що вимоги, які надійшли, знаходяться в черзі обмежений час, після чого, не дочекавшись обслуговування, залишають систему.

Отже, тип задачі масового обслуговування визначається за такими ознаками:

1) характеристикою вхідного потоку;

2) часом обслуговування вимог;

3) числом каналів обслуговування;

4) порядком утворення черги вимог та обслуговування;

5) характеристикою вихідного потоку.

Відомо, що процес надходження вимог носить випадковий характер, і його математична модель є функцією х(t), яка дорівнює числу вимог, що надходять у систему за проміжок часу (0, t). На прак­тиці дуже часто використовують простий потік вимог, який має такі властивості: стаціонарність, відсутність наслідків та ординарність.

Властивість стаціонарності полягає в тому, що ймовірність надход­ження будь-якої кількості вимог протягом певного часу не залежить від початку відліку часу, а тільки від довжини цього проміжку. Отже, ймовірність появи k вимог протягом проміжку часу від t₀ до t₀ + t не залежить від t₀і є функцією тільки параметрів k i t.

Властивість відсутності наслідків полягає в тому, що ймовірність надходження k вимог протягом проміжку часу t₀, t₀+t не залежить від того, скільки було вимог іяк вони поступали до цього проміжку. Ординарність потоку вимог виражається умовою практичної неможливості появи двох або декількох вимог в один і той самий мо­мент.

Порівнюючи властивості простого потоку із властивостями розподілу Пуассона, можна переконатися в їх ідентичності. Тому математично простий потік можна представити як Пуассонівський розподіл.

, k  = 1, 2, …, m;

де: λ – інтенсивність потоку, тобто середнє число вимог за одиницю часу;

Р_k(t) – імовірність надходження k вимог за проміжок часу (0, t).

У системі управління виробництвом, як правило, необхідно вміти кількісно оцінити ефективність функціонування діючої системи обслуговування з очікуванням. Для цього необхідно розрахувати середні значення параметрів:

1) кількість вимог у черзі та системі;

2) час очікування вимог у черзі;

3) число незайнятих каналів обслуговування;

4) коефіцієнти простою в черзі та системі;

5) коефіцієнти простою каналів обслуговування.

Розглянемо систему, яка складається з S каналів обслуговування. Кожен з каналів може одночасно обслужити тільки одну вимогу. В систему поступає обмежений потік вимог (не більше m вимог) з інтенсивністю λ. Вимога, яка надійшла в систему і застала хоча б один канал вільним, відразу надходить на обслуговування. Якщо всі канали зайняті, вимога ставиться в чергу і обслуговується тільки після то­го, коли будуть задоволені всі вимоги, що надійшли раніше. Середня кількість вимог, що обслуговуються одним каналомза одиницю часу, становить μ. Отже, інтенсивність обслуговування буде:

ρ = λ/μ.

Час обслуговування розподіляється за показниковим законом.

У даному випадку кількість вимог у системі обмежена величиною m і, як наслідок, система може знаходитись у довільний момент часу в од­ному із m + 1 станів.

Розглянемо розрахунок кількісних оцінок у випадку одноканальної системи обслуговування з обмеженою кількістю вимог.

1. Ймовірність того, що в системі знаходиться k вимог:

P_k = (m – k + 1) ·ρ·P_k-1, 1£ k £ m.

2. Ймовірність того, що в системі немає жодної вимоги:

3. Математичне сподівання кількості вимог у черзі (середня довжина черги):

.

4. Математичне сподівання кількості вимог у черзі та на обслугову­ванні (в системі):

.

5. Математичне сподівання простою каналів обслуговування:

.

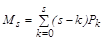6. Середній час очікування вимог у черзі:

.

7. Коефіцієнт простою вимог у черзі:

L_r = M_r / m.

8. Коефіцієнт простою вимог у системі:

L_c = M_c / k.

9. Коефіцієнт простою каналів обслуговування:

L_s = M_s / s.

Перейдемо до розрахунку параметрів багатоканальної системи з обмеженою кількістю вимог обслуговування. Порівняно з одноканальною системою виняток складають тільки розрахунки Р_k і Р₀. Ці величини розраховуються відповідно до формул:

Р_k = а_k Р₀.

причому а₀ = 1;

 .

Інші параметри оцінюються за наведеними вище формулами.

Приклад. У цеху 7 однотипних устаткувань, які працюють незалежно одне від одного. Неполадки, які виникають в устаткуванні, носять випадковий характер і розподіляються за законом Пуассона. Протягом однієї години в середньому виходитьз ладу 2 одиниці устаткування. Ці неполадки ліквідовуються одним механіком, який може обслужити протягом однієї години 8 вимог.

Необхідно розрахувати: коефіцієнти простою вимог у черзі та системі, коефіцієнт простою механіка та середній час очікування вимог у черзі.

Розв’язання. Відповідно до наведених позначень та умови задач, маємо:

S = 1; λ = 2; μ = 8; m = 7.

Знайдемо інтенсивність обслуговування: ρ = λ/μ = 2/8 = 0,25.

Знайдемо P_0­ :

= =

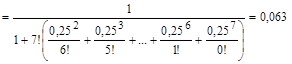
Таким чином, ймовірність того, що в системі не буде жодної вимо­ги, або все устаткування справне, буде 0,063. На основі формули
P_k = (m – k + 1) ·ρ·P_k-1, 1£ k £ m знайдемо P_k:

Р_k = (7 – k + 1) 0,25Р_k-1, k = 1, 2, ...,7;

Р₁  = (7 – 1 + 1) 0,25Р₀ =  0,11;       Р₂  = (7 – 2 + 1) 0,25Р₁ = 0,165;

Р₃  = (7 – 3 + 1) 0,25Р₂ =  0,206;    Р₄  = (7 – 4 + 1) 0,25Р₃ = 0,206;

Р₅  = (7 – 5 + 1) 0,25Р₄ = 0,154;     Р₆  = (7– 6 + 1) 0,25Р₅ = 0,077;

Р₇  = (7 – 7 + 1) 0,25Р₆ = 0,019.

Обчисливши значення Р_k, можемо перейти до визначення основних числових характеристик заданої системи обслуговуван­ня. Так, математичне сподівання кількості вимог у черзі

 Р₂ + 2Р₃ + 3Р₄ + 4Р₅ + 5Р₆ + 6Р₇ = 2,31.

 Отже, в середньому в черзі простоює 2,31 вимог. Коефіцієнт простою вимог у черзі: L_r = M_r / m = 2,31 / 7 = 0,33.

Тобто 33% робочого часу через неполадки устаткування простоює в черзі, чекаючи на обслуговування.

Визначимо коефіцієнт простою устаткування в системі. Для цього спочатку необхідно обчислити математичне сподівання кількості ви­мог у системі (в черзі на обслуговування):

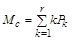= Р₁ + 2Р₂ + 3Р₃ + 4Р₄ + 5Р₅ + 6Р₆ + 7Р₇ = 3,247.

Таким чином, у середньому в черзі та на обслуговуванні простоює 3,247 устаткування. Коефіцієнт простою устаткування в системі стано­вить L_c = Mc / m = 3,247 / 7 = 0,46.

Для визначення коефіцієнта простою каналів обслуговування не­обхідно знайти математичне очікування простою каналів обслугову­вання в системі. У нашому випадку одноканальної системи обслугову­вання отримаємо:

 = P₀  = 0,063.      Отже, L_s = М_s / s = 0,063.

Таким чином, у середньому механік простоює 6,3% робочого часу, що свідчить про його високу завантаженість.

Знайдемо середній час очікування вимог у черзі:

Як бачимо, при існуючій організації проведення ремонтних робіт устаткування велику частину робочого часу витрачають на усунення неполадок, що призводить до значних економічних витрат. Зменшити витрати можна за допомогою збільшення кількості каналів обслуговування, тобто кількості механіків. Таким чином, виникає задача багатока­нальної системи обслуговування.

Припустимо, що в цеху працює два механіки з однаковою продуктивністю. Вхідні параметри системи залишаються незмінними.

Для знаходження числових характеристик багатоканальної системи насамперед визначимо імовірність того, що в систему поступить k вимог
(1 ≤ k ≤ 7). Відомо, що

, а₀ = 1, s = 2.

Знайдемо значення коефіцієнтів а_k:

              

         

         

.

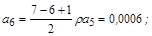
Тоді ;

Р₁ = а₁ Р₀ = 0,37441; Р₂ = а₂ Р₀ = 0,14041; Р₃ = а₃ Р₀ = 0,0439;

Р₄ = а₄ Р₀ = 0,011; Р₅ = а₅ Р₀ = 0,00206; Р₆ = а₆ Р₀ = 0,00026;

Р₇ = а₇ Р₀ = 0,00002.

Обчислимо значення M_r, M_c i M_s:

;

;

.

Коефіцієнт простою устаткування в очікуванні ремонту:

.

Коефіцієнт простою устаткування в системі:

.

Коефіцієнт простою механіків:

.

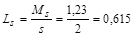Середній час очікування вимог у черзі:

Отже, використання в ремонті додатково ще одного механіка дозволить більш ефективно використовувати у виробничому процесі наявний парк устаткування. В той же час 61,5% свого робочого часу механіки будуть простоювати.

Одержані дані можуть бути використані для покращення організації виробничого процесу.

Для визначення оптимальної кількості каналів обслуговування послідовність дій буде наступною:

1. Для заданої системи масового обслуговування послідовно розгля­дається різна кількість каналів обслуговування (S = 1, 2, …, n).

2. Для кожної кількості каналів розраховуються основні параметри систем обслуговування, в тому числі середній час простою вимоги в системі .

3. Встановлюється середня вартість витрат С_т внаслідок простою вимог за одиницю часу.

4. Визначаються витрати на утримання одного каналу обслуговування С _k за одиницю часу.

5. Розраховується величина втрат, пов’язана з простоєм вимог при кількості каналів S за період Т:

L _{t s} = C_т ·  ·T·λ.

6. Обчислюються сумарні затрати на утриманняS каналів обслуго­вування за період Т:

L_ks = C_k· S · T.

7. Знаходяться сумарні витрати в системі обслуговування при різній кількості каналів:

L_s = L_ts + L_ks.

8. Вибирають мінімальні витрати L = min, яким відповідає оптимальне значення числа каналів обслуговування.

Зробимо розрахунок оптимального числа механіків за даними умовного прикладу в таб. 1.18.

 

Таблиця 1.18

Розрахунок оптимального числа механіків

Показники	Кількість механіків
	1	2
1. Середній час простою устаткування, год	0,307	0,0059
2. Середньогодинна продуктивність одиниці устаткування, грн.	500	500
3. Середня величина недоданої продукції в зв’язку з простоєм устаткування, грн. (п.1 х п. 2)	153,5	2,95
4. Середньогодинна ставка оплати механіка, грн.	5	5
5. Сума заробітної плати механіків за зміну, грн. (п. 4 х 8* х кількість механіків)	40	80
6. Всього витрат, грн. (п. 3 + п. 5)	193,5	32,92

 

8* – тривалість робочого дня, год

Розрахунок показує, що мінімальна сума витрат досягається при умові утримання двох механіків.

 

---

Дата добавления: 2019-02-12; просмотров: 242; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!