Переміщення під час рівноприскореного руху
 Ми знаємо із 9 класу:
Ми знаємо із 9 класу:
Для будь-якого руху проекція переміщення чисельно дорівнює площі фігури під графіком залежності  .
.
Розглянемо рівноприскорений рух, за якого початкова швидкість і прискорення мають однаковий напрямок із віссю OX.
1. Розіб’ємо весь час руху тіла на невеликі інтервали часу 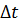 . .
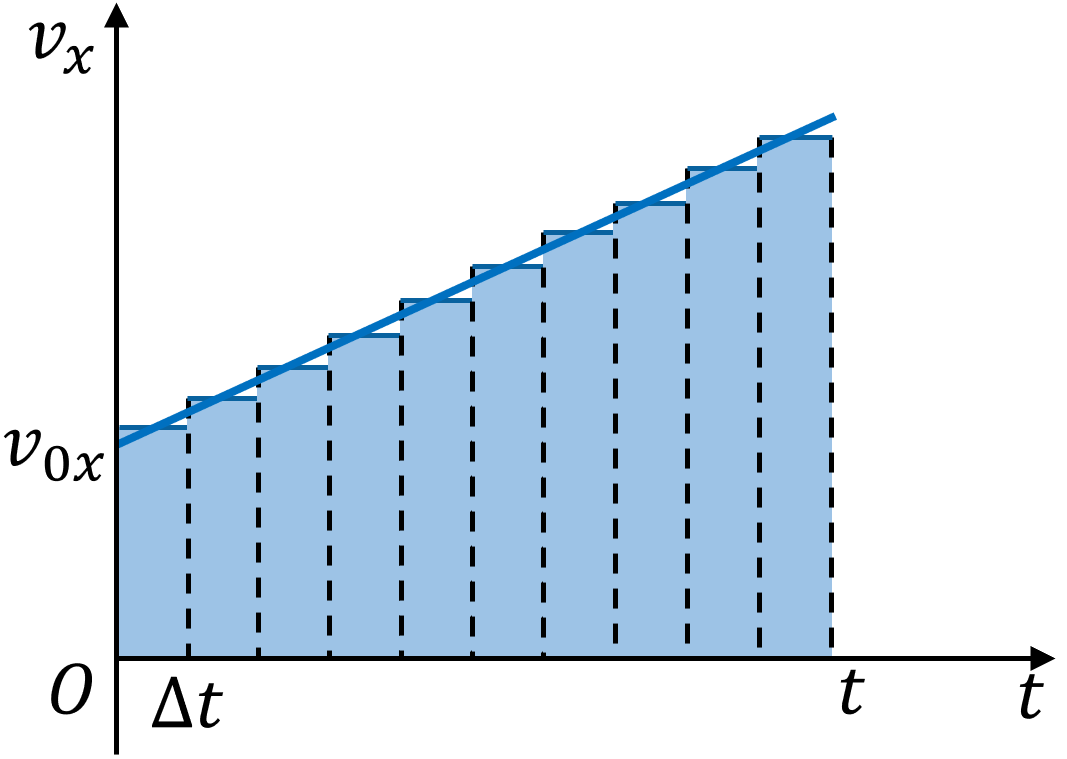
| 2. Припустимо, що протягом кожного інтервалу часу швидкість руху тіла залишалася незмінною. Загальне переміщення під час такого уявного руху дорівнює сумі площ смужок завширшки 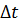 , які разом утворюють східчасту фігуру. , які разом утворюють східчасту фігуру.
|

| 
|
4. У результаті нескінченного зменшення інтервалів часу  східчаста фігура «перетвориться» на трапецію, а переміщення чисельно дорівнюватиме площі цієї трапеції. східчаста фігура «перетвориться» на трапецію, а переміщення чисельно дорівнюватиме площі цієї трапеції.
| 3. Якщо зменшити інтервали часу 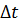 то переміщення, як і раніше, дорівнюватиме площі східчастої фігури, яка поступово набуває вигляду трапеції. то переміщення, як і раніше, дорівнюватиме площі східчастої фігури, яка поступово набуває вигляду трапеції.
|

| 
|
В разі рівноприскореного руху проекція переміщення чисельно дорівнює площі трапеції:



Рівняння проекції переміщення:

 Графік проекції переміщення в разі рівноприскореного прямолінійного руху – парабола.
Графік проекції переміщення в разі рівноприскореного прямолінійного руху – парабола.
Якщо  , то вітки параболи напрямлені вгору.
, то вітки параболи напрямлені вгору.
Якщо  , то вітки параболи напрямлені вниз
, то вітки параболи напрямлені вниз
Скориставшись означенням прискорення та формулою (1), можна отримати ще одну формулу для обчислення переміщення.



|
|
|
Рівняння координати
Для будь-якого виду руху проекція переміщення і координата пов’язані співвідношенням:

 – початкова координата (координата тіла в момент початку спостереження);
– початкова координата (координата тіла в момент початку спостереження);
 – проекція переміщення.
– проекція переміщення.

Для рівноприскореного руху 
Рівняння координати для рівноприскореного прямолінійного руху:

Проаналізувавши останнє рівняння, доходимо висновку, що залежність x(t) є квадратичною, тому графік координати – парабола.
ІV. ЗАКРІПЛЕННЯ НОВИХ ЗНАНЬ І ВМІНЬ
Рух тіл вважайте рівноприскореним прямолінійним.
1. Тролейбус, рухаючись зі швидкістю 18 км/год, зупинився за 4 с. Визначте прискорення його руху та гальмівний шлях тролейбуса.
Дано:



| Розв’язання
Відповідь: |

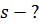
|
2. Залежність швидкості руху тіла від часу має вигляд:  . Визначте параметри руху тіла та охарактеризуйте його.
. Визначте параметри руху тіла та охарактеризуйте його.
Дано:

| Розв’язання Порівняємо задане в умові задачі рівняння з рівнянням швидкості для рівноприскореного прямолінійного руху:
Тіло рухається у напрямку координатної осі
Відповідь:
| ||


|
3. Координата тіла, що рухається, змінюється згідно з рівнянням 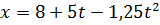 . Визначте параметри руху тіла, охарактеризуйте його, запишіть рівняння залежності швидкості руху від часу та побудуйте графік залежності
. Визначте параметри руху тіла, охарактеризуйте його, запишіть рівняння залежності швидкості руху від часу та побудуйте графік залежності  .
.
Дано:
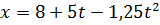
| Розв’язання Наведене рівняння відповідає рівнянню рівноприскореного прямолінійного руху, яке має вигляд:
Вважаючи, що всі величини дано в СІ, бачимо, що
Формула миттєвої швидкості під час рівноприскореного прямолінійного руху має вигляд:
Для побудови графіка такого рівняння достатньо знайти координати двох точок цього графіка, позначити ці точки на координатній площині і провести через них пряму.
| ||||||




|
4. За графіком залежності швидкості від часу, який наведено на рисунку, охарактеризуйте рух тіла, визначте початкову швидкість, прискорення його руху та запишіть рівняння  .
.
|
|
|
 Розв’язання
Розв’язання




Тіло рухається у напрямку координатної осі 
 рівноприскорено (
рівноприскорено (  ;
;  , швидкість руху зменшується)
, швидкість руху зменшується)
Відповідь: 
V. ПІДБИТТЯ ПІДСУМКІВ УРОКУ
Бесіда за питаннями
1. Який рух називають рівноприскореним прямолінійним?
2. Охарактеризуйте прискорення як фізичну величину.
3. Як рухається тіло, якщо напрямок його прискорення: а) збігається з напрямком руху? б) протилежний напрямку руху? в) якщо прискорення тіла дорівнює нулю?
4. Запишіть рівняння залежності  для рівноприскореного прямолінійного руху. Який вигляд має графік цієї залежності?
для рівноприскореного прямолінійного руху. Який вигляд має графік цієї залежності?
5. За допомогою яких формул можна обчислити проекцію переміщення? Виведіть ці формули.
6. Доведіть, що графіком залежності  є парабола. Як напрямлені її вітки? Якому моменту руху відповідає вершина?
є парабола. Як напрямлені її вітки? Якому моменту руху відповідає вершина?
7. Запишіть рівняння координати для рівноприскореного прямолінійного руху. Назвіть фізичні величини, які пов’язує це рівняння.
VI. Домашнє завдання
Опрацювати § 6, Пункт 4 Задача 1, Вправа № 6 (1)
Дата добавления: 2019-01-14; просмотров: 930; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!









 .
. 

 .
. 



 За параметрами руху тіла та графіком швидкості робимо висновок: тіло рухається у напрямку координатної осі
За параметрами руху тіла та графіком швидкості робимо висновок: тіло рухається у напрямку координатної осі  рівноприскорено (
рівноприскорено ( 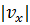 лінійно зростає) проти координатної осі
лінійно зростає) проти координатної осі  .
.