Алгебраические понятия, важные для суперизации

⇐ ПредыдущаяСтр 4 из 4

Определение свойства когерентности пучков, изначально сформулированное с топологической точки зрения, допускает алгебраизацию. Для этого мы в качестве мультипликативно замкнутого подмножества S возьмем систему степеней элемента 𝑓 из кольца А. Тогда вместо модуля M_S (его построение см. в начале § 1.3.) мы будем писать M_𝑓, который является A_𝑓-модулем. Поскольку, при S⊂S', каждому гомоморфизму A_S→A_S_' мы сопоставляем гомоморфизм M_S→M_S_', то А-модулю М мы можем сопоставить пучок 𝓜 над X=SpecA.

Это, в некотором смысле, обратная конструкция и поэтому требует для построения пучка 𝓜 ввести понятие из теории категорий проективного (обратного) предела, который, в свою очередь, можно интерпретировать, как двойственный к уже встречавшемуся у нас индуктивному (прямому) пределу. Если у нас задана, например, последовательность абелевых групп {A_n} и их морфизмов ⍺_n₊₁:A_n₊₁→A_n, то можно говорить, что у нас задана соответствующая проективная система (A_n, ⍺_n). Тогда множество последовательностей {a_n}, где a_n∈A_n, таких, что ⍺_n₊₁(a_n₊₁)=a_n, образуют группу, которая и называется проективным пределом проективной системы (A_n, ⍺_n). Другими словами, мы строим некоторый новый объект по семейству, индексированному направленным множеством I, однотипных объектов A_i и набору отображений A_j→A_i, i≤j и i, j∈I. Более строго, пусть I – направленное множество с отношением порядка ≤, и пусть каждому i∈I сопоставлена алгебраическая система A_i какого либо фиксированного класса (абелевых групп, А-модулей и т.п.), причем каждой паре (i, j), такой, что i≤j и i, j∈I, сопоставлен гомоморфизм ⍺_ij:A_j→A_i с двумя условиями: ⍺_ii=id для любого i∈I и ⍺_ik=⍺_ij∘⍺_jk для любых i≤j≤k и i, j , k∈I. Тогда множество-носитель проективного предела данного направленного семейства – это фактормножество А прямого произведения A_i по транзитивному замыканию отношения эквивалентности, говорящему, что каждый элемент эквивалентен меньшим элементам в соответствии с отношением порядка ≤, что можно записать, как:

proj lim A_i = {(x_i)∈ 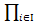A_i │ x_i = ⍺_ij(x_j) ∀ i≤j}.

Существуют канонические проекции 𝜋_i:A→A_i, которые выбирают i-ю компоненту прямого произведения для каждого i∈I. Алгебраическая структура на проективном пределе восстанавливается исходя из того, что эти проекции 𝜋_i являются гомоморфизмами. Поскольку мы будем использовать проективный предел для построения пучка, нам нужно иметь его определение в категорном смысле. Делается это при помощи его универсального свойства, а именно, пусть (A_i, ⍺_ij) – семейство объектов и морфизмов категории K с условиями, что каждой паре (i, j), такой, что i≤j и i, j∈I, сопоставлен гомоморфизм ⍺_ij:A_j→A_i, причем: ⍺_ii=id для любого i∈I и ⍺_ik=⍺_ij∘⍺_jk для любых i≤j≤k и i, j , k∈I. Тогда А называется проективным пределом системы (A_i, ⍺_ij), который мы будем записывать как А = proj lim A_i, если выполнены следующие два условия:

(I) Существует такое семейство отображений 𝜋_i:A→A_i, что 𝜋_i=⍺_ij∘𝜋_j для любых i≤j;

(II) Для любого семейства отображений 𝜓_i:B→A_i произвольного множества B, для которого выполнены равенства 𝜓_i=⍺_ij∘𝜓_j для любых i≤j, существует единственное отображение 𝑢:B→A, такое, что 𝜓_i=𝜋_i∘𝑢 для всех i∈I.

Таким образом, мы имеем следующую коммутативную диаграмму, описывающую универсальное свойство проективного предела системы (A_i, ⍺_ij):

𝑢

𝜓_j A 𝜓_i

𝜋_j 𝜋_i

A_j A_i

⍺_ij

Примером проективного предела является инициальная топология на соответствующем множестве-носителе в категории Top.

Приведем еще один пример – кольцо формальных степенных рядов R[[t]] над коммутативным кольцом R является проективным пределом факторколец R[t]∕tⁿR[t], которые индексированы натуральными числами n и с естественными проекциями вида R[t]∕tⁿ⁺^jR[t]→R[t]∕tⁿR[t]. Поскольку именно этот пример очень актуален для нас при построении искомого пучка 𝓜, сделаем короткое замечание относительно формальных степенных рядов. По определению, формальный степенной ряд – это формальное алгебраическое выражение вида:

F(X) = a_nXⁿ, a_n∈R, где R – некоторое кольцо.

Формальный степенной ряд не имеет числовых значений (а, следовательно, и не рассматриваются вопросы его сходимости), но для него определены алгебраические операции, если F=F(X)= a_nXⁿ, G=G(X)= b_nXⁿ, H=H(X)= c_nXⁿ, то:

(I) Сложение: H = F+G ⟺ ∀n c_n = a_n + b_n;

(II) Умножение: H = FG ⟺ ∀n c_n = 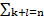a_kb_l;

(III) Дифференцирование: H = F' ⟺ ∀n c_n = (n+1)a_n₊₁;

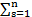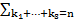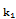(IV) Композиция: H = F∘G ⟺ ∀n c_n = a_s b 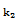b … b 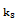, b₀=0.

Таким образом, формальные степенные ряды над кольцом R образуют кольцо R[[X]]. Понятно, что за X мы можем принять модуль [t], порожденный элементом t (и его степенями) и получим кольцо R[[t]] из нашего примера.

Кольцо R[[X]] можно превратить в топологическое, если задать метрику в виде равенства d((a_n), (b_n))=2⁻^k, где k наименьше натуральное число, такое, что a_k≠b_k. Умножение и сложение в топологии, порожденной данной метрикой d являются непрерывными и формальные степенные ряды в такой топологии образуют топологическое кольцо R[[X]]. Также важно отметить, что формальный степенной ряд a_nXⁿ в кольце R[[X]] является обратимым тогда и только тогда, когда в кольце R является обратимым его элемент a₀. Необходимость следует из того, что свободный член произведения равен a₀b₀, а достаточность следует из того, что коэффициенты обращенного ряда определяются по формулам:

b₀ = 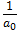, b₀ = −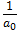 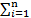a _i b_n-i ∀n≥1.

Приведем свойства для формальных степенных рядов над кольцом R, в том числе и свойства кольца R[[X]], рассматриваемого как топологическое кольцо:

(I) Если R – нётерово кольцо, то и кольцо R[[X]] – нётерово;

(II) Если R – целостное кольцо, то и кольцо R[[X]] – целостное;

(III) Если R – локальное кольцо, то и кольцо R[[X]] – локальное;

(IV) Если R – конечное кольцо, то кольцо R[[X]] является компактным;

(V) Топологическое метрическое пространство (R[[X]], d) является полным.

Чтобы построить пучок 𝓜, мы положим для каждого открытого множества U=D(𝑓) (в топологии Зарисского) равенство 𝓜(U)=M_𝑓 и рассмотрим все элементы 𝑓 для которых D(𝑓)⊂U. Для них определены гомоморфизмы ограничения M_g→M_𝑓 при D(g)⊃D(𝑓). Определим проективный предел

𝓜(U) = proj lim _D₍_𝑓₎_⊂_U M_𝑓.

Этот проективный предел 𝓜(U) является модулем над кольцом Q(U), который, в свою очередь, является проективным пределом Q(U)=proj lim _D₍_𝑓₎_⊂_U A_𝑓. Включения U⊂V определяют ограничения ρ│ 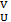:𝓜(V)→𝓜(U), а система локальных модулей и соответствующих ограничений (𝓜(U), ρ) определяет искомый пучок модулей 𝓜 над пучком колец Q(X)=Q(SpecA). Используемые гомоморфизмы ограничений должны быть пронумерованы целыми числами и их должно быть конечное число, т.е. нам всегда будет требоваться свойство бикомпактности для X.

Определив пучок 𝓜, используя понятие проективного предела, мы очевидно замечаем, что целесообразно использовать свойство нётеровости. А именно, схема 𝒳 называется нётеровой, если она обладает таким конечным покрытием аффинными открытыми множествами X=⋃U_i, U_i=SpecA_i (т.е. областями в 𝔸ⁿ, n-мерном аффинном пространстве над полем 𝕂, состоящими из точек (a₁, … , a_n), a_i∈𝕂), что все кольца A_i являются нётеровыми. Пучок Q(X)-модулей 𝓕 на нётеровой схеме 𝒳=(X, Q(X)) называется квазикогерентным, если существует такое покрытие X открытыми аффинными подмножествами U_i=SpecA_i, что для каждого i существует A_i-модуль M_i, такой, что 𝓕∣_Ui=𝓜_i.

Заметим, что если A_i – алгебра конечного типа над кольцом B, то и 𝒳 является схемой конечного типа. В случае нётеровости кольца B, схема конечного типа становится нётеровой, поэтому мы рассматриваем именно нётеровы схемы. Учитывая сказанное мы можем принять следующее определение – квазикогерентный пучок 𝓕 называется когерентным, если каждый из модулей M_i является конечно порожденным A_i-модулем.

В дальнейшем мы также будем интересоваться комплексным случаем, поэтому дадим необходимые определения. Будем использовать определения из комплексного анализа, где голоморфная функция (иногда называемая регулярной) – функция комплексного переменного, определённая на открытом подмножестве комплексного пространства ℂⁿ комплексно дифференцируемая в каждой точке. Голоморфные функции также называют иногда аналитическими (т.е. могут быть представлены сходящимися к ним рядами Тейлора), но аналитическая функция не обязана быть определена на множестве комплексных чисел. Для комплексных функций комплексной переменной множества голоморфных и аналитических функций совпадают. Производная голоморфной функции опять является голоморфной, поэтому голоморфные функции являются бесконечно дифференцируемыми в своей области определения.

Пусть G – область в n-мерном пространстве ℂⁿ и Q(G) – пучок ростков голоморфных функций на G, тогда пара (G, Q(G)) – окольцованное пространство, являющееся областью в ℂⁿ. Зададим в G подмножество M, определяемое уравнениями 𝑓_i(z₁, … , z_n)=0, i=1,…,k, где 𝑓_i – голоморфные функции на G, и положим Q(M)=Q(G)∕𝔊│_M, где 𝔊 – подпучок идеалов в Q(G), порожденный 𝑓_i. Полученное окольцованное пространство (M, Q(M)) называется аналитическим множеством в G. Соответственно, комплексным пространством назовем хаусдорфово топологическое пространство X, наделенное структурным пучком комплексных алгебр Q(X) так, что каждая точка в X имеет открытую окрестность, изоморфную, как окольцованное пространство, аналитическому множеству в области пространства ℂⁿ. В целом можно утверждать, что по отношению к комплексному пространству аналитические множества играют роль локальных моделей, о которых мы говорили в первой части настоящей работы. Если в качестве локальных моделей взять области в пространстве ℂⁿ, то мы получим определение комплексного многообразия.

Практически всегда аналитическое суперпространство есть такое суперпространство (M, Q(M)), что (M, Q(M) ) является комплексным пространством, а Q(M) является когерентным пучком Q(M) -модулей. Аналогично выглядит ситуация для алгебраического суперпространства, где пара с четной частью пучка является алгебраическим пространством и для суперсхемы, где четная часть пучка является схемой, а нечетные части пучков являются соответствующими когерентными пучками Q(M) -модулей.

Уточним, как устроено градуировка для пучка Q(M)-модулей. Пусть (M, Q(M)) – суперпространство и 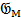=Q(M) +[Q(M) ]² – пучок идеалов в Q(M). Тогда построив пучок Gr Q(M)=Q(M)∕ 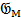, мы получим M_p=(M, Gr Q(M)) – чисто четное суперпространство. Обобщая, введем окольцованное пространство, у которого структурный пучок ℤ-градуирован, это будет пара

GrM = (M, GrQ(M)) = (M, ⊕_i_≥₀Gr_iM), Gr_iM = ∕ .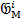

Говоря о GrM как о суперпространстве мы, конечно, подразумеваем градуировку ℤ mod 2. Пусть теперь ℰ пучок Q(M)-модулей. Определим для него градуировку в виде:

Grℰ = ⊕_i_≥₀Gr_iℰ = ∕ .

Как мы увидим в дальнейшем, компонентный анализ, т.е. информация о градуированных объектах, оказывается очень полезным. Для изучения внутренней структуры супермногообразия нам потребуется обобщить понятие группы Пикара, что даст нам новые полезные инварианты. Приведем основные сведения в отношении этой группы из классического случая. Для этого нам потребуется еще одно важное понятие из алгебраической геометрии – дивизоры. Дивизоры могут быть определены различными способами, мы будем использовать достаточно общий случай – дивизоры Картье.

Пусть 𝒳=(X, Q(X)) – некоторая схема. И пусть каждого аффинного подмножества у нас задана мультипликативная система , образованная множеством всех элементов из кольца , не являющимися делителями нуля. Тогда мы получим полное кольцо частных….

Дата добавления: 2018-10-27; просмотров: 252; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!