Геометрическое и физическое подобие.
Напомним, что геометрически подобными фигурами считаются такие, у которых отношение сходственных геометрических размеров остается постоянным при изменении их размеров. Это дает возможность преобразования одной фигуры в другую, подобную ей фигуру. Условия такого преобразования были сформулированы в 1872 г. Феликсом Клейном. При этих преобразованиях инварианты этих фигур, характеризующие их форму, остаются неизменными. Любая геометрия это теория инвариантов особой группы преобразований. Следуя этому, в теории подобия нужно рассматривать группу преобразований подобия в инварианты подобия.
В классической теории геометрического подобия группа преобразований подобия включает себя изменение масштаба, а инвариантом является форма фигуры. Между элементами геометрически подобных фигур можно установить взаимно - однозначное соответствие, и, следовательно, они изоморфны между собой. Учитывая это, можно рассматривать перенос представлений о геометрическом подобии в область физических явлений как попытку создания прикладной теории изоморфных (или гомоморфных) объектов. Следуя Ф. Клейну, такую теорию нужно строить как теорию инвариантов группы физически подобных преобразований. Чтобы теория стала прикладной, в нее надо включить выработку правил (алгоритмов):
1) Нахождения инвариантов указанных преобразований для «натуры», которую в дальнейшем будем называть оригиналом.
|
|
|
2) Сохранения их неизменности в модели.
Таков первоначальный план теории подобия и моделирования.
Уточним понятие «физически подобные преобразования». В математике преобразование понимается, как установление соответствия между элементами двух множеств. При этом каждому элементу одного множества ставится в соответствие элемент другого (или того же) множества из семейства множеств, произвольной природы. Геометрически подобное преобразование состоит, в изменении всех расстояний в постоянном отношении К. Будем называть это соотношение коэффициентом подобия. Таким образом, преобразуемой величиной здесь оказывается линейный размер или протяженность. При подобном преобразовании физических явлений в объекте необходимо изменять не только пространственные переменные, но и все физические величины, существенные для моделируемого явления. При этом для каждой физической величины необходимо вводить свой коэффициент подобия. Результат такого преобразования - объект, физически подобный преобразуемому, должен соответствовать принципу математического изоморфизма: математическое описание модели и объекта должны быть одинаковыми. Поясним эти положения примером.
|
|
|
Пример:
Пусть оригинал – механическая система, поведение которой описывается вторым законом Ньютона:
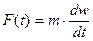(2.1)
где F(t) - внешняя сила, действующая на систему;
m –масса системы
w – скорость,
t – время,
Модель, математически изоморфная оригиналу, также должна подчиняться уравнению (2.1). Поэтому, для сопоставляемой пары объектов мы можем записать следующую пару уравнений:
; 
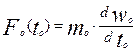; (2.2)
Здесь индекс «о» относится к объекту, а индекс «М» к модели. Введем коэффициенты подобия для всех величин, входящих в уравнения (2.2):
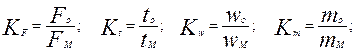(2.3)
Заменим все переменные в уравнении (2.2) для модели на переменные для объекта, выраженные через коэффициенты подобия К:
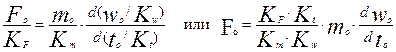(2.4)
Уравнение (2.4) эквивалентно уравнению модели, приведенному выше. Оно будет тождественно уравнению оригинала, если станет математически изоморфным оригиналу, если при разработке модели удастся обеспечить равенство:
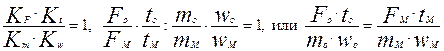
Представим себе, что создается несколько разномасштабных моделей М1, М2,… изучаемой системы. Тогда нетрудно показать простыми выкладками, что в этом случае будут соблюдаться соотношения:
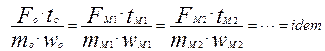(2.5)
Получена специфическая функция (обозначим ее Ne от Newton), которая является инвариантом нашего подобного преобразования, инвариантом физического преобразования систем, подчиняющихся уравнению (2.1)
|
|
|
(2.6)
Эта функция представляет отношение важных механических характеристик моделируемой системы: импульса силы F×t к импульсу тела m×w. Заменив в формуле (2.6) время t через расстояние l и скорость w, t=l/w, можно получить иную форму записи инварианта подобия:
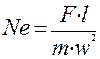(2.7)
В этом случае этот инвариант обозначает отношение работы силы F на расстоянии l к удвоенной кинетической энергии системы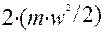 
. Работа численно равна изменению энергии, и это отношение имеет смысл отвлеченного безразмерного числа, характеризующего убыль энергии в долях от ее запаса в движущейся системе.
Из рассмотренного примера можно сделать три вывода:
1). Инварианты физического подобия представляют собой специфические комбинации из переменных – физических характеристик оригинала, степенные одночлены, например следующего вида:
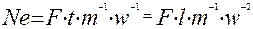(2.8)
2) Указанные комбинации переменных можно интерпретировать как отношение двух фундаментальных величин одинаковой размерности, как меру соотношения интенсивностей, сил, энергий и т.д.
3) Инварианты физического подобия представляют собой отвлеченные безразмерные числа.
В теории подобия указанные инварианты называются критериями подобия.
|
|
|
Первый из выводов в теории подобия формулируется в виде так называемой первой теоремы подобия:
Инвариантами преобразования физического подобия являются критерии подобия.
Задачу моделирования можно подразделить на две:
1. Разработка модели изучаемого процесса или аппарата.
2. Собственно моделирование, которое включает в себя:
а) получение искомых результатов с помощью модели.
б) перенос этих результатов с модели на оригинал
Теория подобия формулирует основные приемы и правила указанных
этапов моделирования:
1. Определить критерии подобия, существенные для моделируемого объекта в данной ситуации.
2. Сформулировать задачу моделирования, соответствующую общей задаче разработки объекта.
3. Оценить пределы изменения выявленных критериев подобия для разрабатываемого объекта.
4. Сформулировать в критериальной форме модель, обеспечивающую равенство определяющих критериев в модели и в объекте.
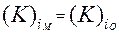(2.9).
Дата добавления: 2014-01-07; просмотров: 9464; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!