Линейные однородные дифференциальные уравнения

Nbsp;                           7. Дифференциальные уравнения                                       7.1.Основные понятия Многие задачи техники, физики, биологии, экономики и социальных наук решаются при помощи дифференциальных уравнений. При этом широко используется физический, геометрический и механический смысл производной.   Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и её производные или дифференциалы:        F ( x , y , y ¢ , y ² … , y n ) = 0   Решением дифференциального уравнения называется функция, которая обращает данное уравнение в тождество. Порядком дифференциального уравнения называется порядок высшей производной входящей в уравнение.  Общим решением или интегралом дифференциального уравнения называется такое решение, которое содержит столько независимых постоянных, каков порядок уравнения. Частным решением называется решение, получаемое из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных можно найти, если заданы начальные значения аргумента и функции. Графиком частного решения дифференциального уравнения называется интегральная кривая. Общему решению соответствует семейство (совокупность) всех интегральных кривых.

Дифференциальные уравнения первого порядка

С разделяющимися переменными

   Дифференциальным уравнением 1-го порядка  называется уравнение, связывающее между собой независимую переменную х, функцию и её производную или дифференциал:

                                   F ( х, у, у ¢ ) = 0

  Данное уравнение называется дифференциальным уравнением первого порядка, так как содержит производную первого порядка.

  Общим решением или общим интегралом называется такое решение, которое

обращает это уравнение в тождество и содержит одну произвольную постоянную.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольной постоянной.

Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши. График частного решения дифференциального уравнения называется интегральной кривой.

Диффренциальным уравнением с разделяющимися переменными называется уравнение вида:

                                                    у ¢ = f ( x ) y ( y ) .

   Если производную функции выразить через дифференциал функции, то уравнение примет вид:

 

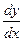= f(x) y (y)

 

  Дифференциальное  уравнение с разделяющимися переменными приводится к дифференциальному уравнению с разделенными переменными:

 

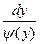=f(x)dx

 

   После интегрирования каждой части уравнения получается решение вида:

y = у (х, С)

 

  Пример

 

Найти общее решение дифференциального уравнения:

 

  3у² dу = 4х³ dх

 

  Решение

  В данном уравнении переменные уже разделены, следовательно нужно проинтегрировать каждую часть уравнения

 

ò3у ² dy = ò 4 x ³ dx

 

     y³ = х⁴ + С

 

  Пример

 

Найти частное решение дифференциального уравнения

 

xdу = уdх ,  если у = 6 при х = 2

 

  Решение

В данном уравнении переменные не разделены, поэтому проведем разделение переменных:

       

   =   ,

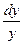Проинтегрируем каждую часть уравнения с использованием таблицы интегралов:

 

ln у = ln x + ln C, так как произвольное постоянное С может принимать

любые численные значения, то для удобства записали lnC.

Пропотенцировав равенство получим общее решение:

y = Сх

Найдем частное решение. Подставим значения х =2 и у = 6 в уравнение, от-

куда получили, что С = 3.

  Запишем частное решение: у = 3х.

   Ответ: частное решение дифференциального уравнения у = 3х.

 

 

           7.3.Однородные дифференциальные уравнения

Первого порядка

Однородной функцией переменных f ( x , y ) называется функция, все члены которой имеют одинаковую степень. Например: f ( x , y ) = 3х²  + 4ху – однородная функция второй степени.

Однородное дифференциальное уравнение  первого порядка имеет вид:

 

                                 f ( x , y ) dx = y ( x , y ) dy ,

 где f ( x , y ) , y ( x , y ) – однородные функции первого порядка.

Однородное дифференциальное  уравнение приводится к дифференциальному уравнению с разделяющимися переменными посредством подстановки у = v • x , где v – новая функция от х.

 

Пример

Найти общее решение однородного уравнения

 

(x+y)dx – xdy = 0

 

Решение

Положим, что у = vx, где v –новая функция от х.

Найдем дифференциал произведения:

dy= xdv + vdx    

 Запишем уравнение с новой функцией v:

 

 (х + vx) dx – x(xdv + vdx) = 0

После преобразований получим:

 

dx – xdv = 0

Разделим переменные:

 dv = , после интегрирования получим: v = lnx + lnC или v = ln(Cx)

Тогда у = х ln(Cx) – общее решение дифференциального уравнения.

 

 7.4. Линейные дифференциальные уравнения первого порядка

 

Линейные дифференциальные уравнения первого порядка имеют вид:

 

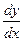                             + f ( x ) × y + y ( x ) = 0

Эти уравнения приводятся к дифференциальным уравнениям с разделяющимися переменными с помощью подстановки y = u • z , где u и z  - новые функции от х.

 

 

Линейные однородные дифференциальные уравнения

---

Дата добавления: 2018-10-27; просмотров: 141; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!