Одноканальная СМО с неограниченной очередью
Рассмотрим одноканальную систему массового обслуживания с ожиданием. Пусть входящий поток заявок на обслуживание – простейший поток с интенсивностью l.
Интенсивность потока обслуживания равна μ. Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Рис.3.4. Граф состояния СМО с неограниченной очередью
Здесь:
l – интенсивность входного потока требований (среднее число заявок на обслуживание, приходящихся на единицу времени).
μ – интенсивность обслуживания (число требований, обслуживаемых в единицу времени).
Состояния:
S0 – канал свободен;
S1 – канал занят, очереди нет;
S2 – канал занят, одна заявка в очереди;
S3 – канал занят, две заявки в очереди;
Sn – канал занят, n-1 заявка в очереди.
Найдём вероятности pk:
Для состояния S0: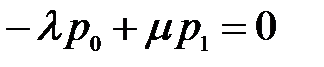 
, отсюда 
;
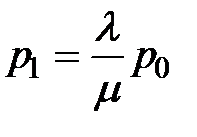Для состояния S1: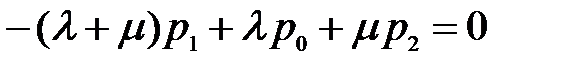 
, подставляем полученное значение для p 1: 
.
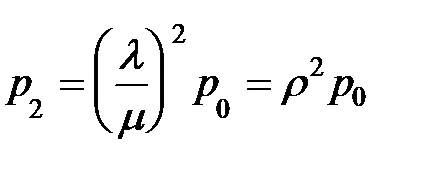Аналогично, для состояния Sk: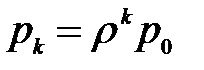 
.
Вероятность p 0 найдём из нормировочного условия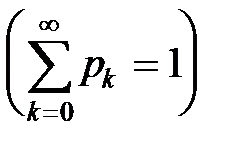 
:
, 
– геометрическая прогрессия, при r < 1 сходится. 
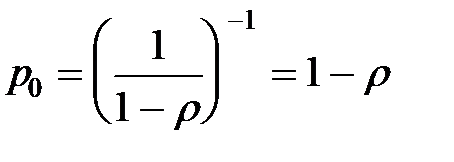– вероятность того, что нет заявок.
r = l/m – мера загрузки одноканальной СМО.
– вероятность того, что прибор занят обслуживанием заявки.
В текущий момент времени в системе может быть 0, 1, 2, ..., k, ... заявок с вероятностями p 0, p 1, p 2, ... .
|
|
|
Математическое ожидание количества заявок:
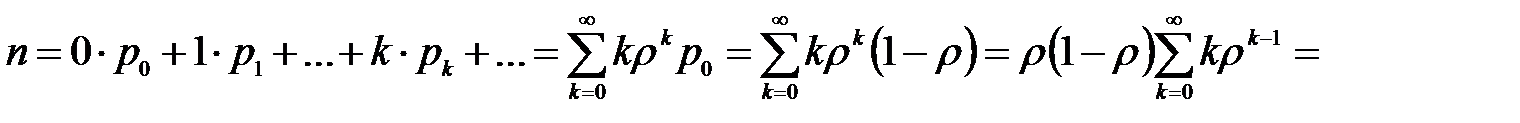
учитывая, что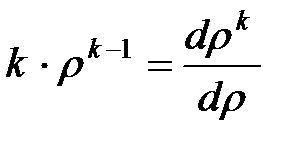 
, получим:
.
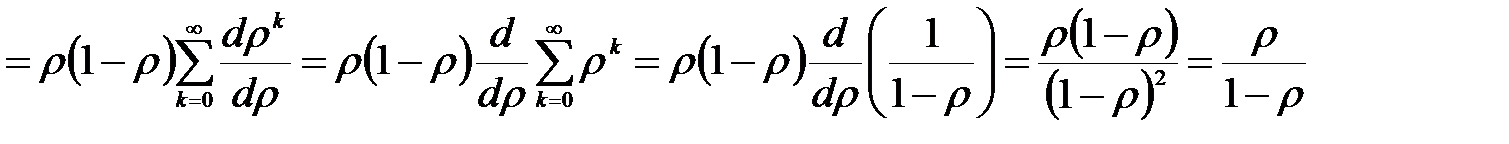Средняя длина очереди равна разности между средним числом заявок в системе и средним числом заявок, находящихся под обслуживанием:
.
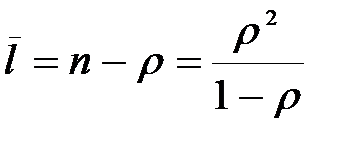Формулы Литтла
|
Рис.3.4 |
Первая формула Литтла позволяет определить время реакции СМО (время пребывания заявки в системе).
Пусть X ( t ) – число заявок, поступивших в СМО до момента времени t, Y ( t ) – покинувших СМО до t. Обе функции случайны и увеличиваются скачком на единицу в моменты прихода и ухода заявок. Тогда число заявок в системе в момент времени t можно определить как: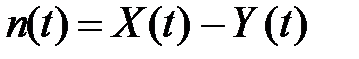 
. Рассмотрим очень большой промежуток времени T и вычислим среднее число заявок в системе:
.
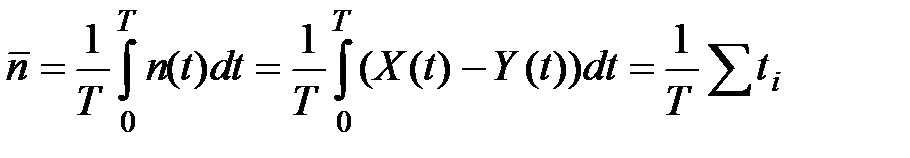Интеграл равен площади ступенчатой фигуры, ограниченной функциями X ( t ) и Y ( t ), эта сумма состоит из прямоугольников, высота которых равна единице, а длина – времени пребывания i-ой заявки в системе ti. Сумма распространяется на все заявки, поступившие в систему за время T. Правую часть домножим и разделим на l: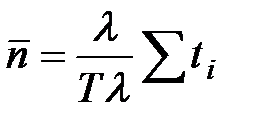 
. T l – среднее количество заявок, пришедших за время T. Поделив сумму всех времён ti на среднее число заявок, получим среднее время пребывания заявки в системе: 
.
|
|
|
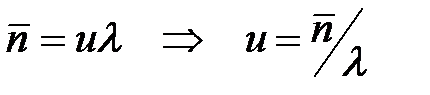Совершенно аналогично можно получить среднее время пребывания заявки в очереди: 
.
Дата добавления: 2018-10-26; просмотров: 255; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!