Консервативные и диссипативные силы. Закон сохранения механичсекой энергии. Условие равновесия механической системы.
Консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)
Консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0.
 работа консервативных сил по произвольному замкнутому контуру равна 0;
работа консервативных сил по произвольному замкнутому контуру равна 0;

Силу  , действующую на материальную точку, называют консервативной или потенциальной, если работа
, действующую на материальную точку, называют консервативной или потенциальной, если работа  , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:
, совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло: 
Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина  меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории
меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории  , например
, например 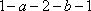 , работа консервативной силы равна нулю .
, работа консервативной силы равна нулю . 
Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.
Диссипативные силы - силы, при действии которых на движущуюся механическую систему её полная механическая энергия убывает, переходя в другие, немеханические формы энергии, например в теплоту.
|
|
|
пример диссипативных сил: сила вязкого или сухого трения.
Закон сохранения механичсекой энергии:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Ek1 + Ep1 = Ek2 + Ep2
Замкнутая система- это система, на которую не действуют внешнии силы или из действие скомпенсировано.
Условие равновесия механической системы:
Статика - раздел механики, изучающмй условия равновесия тел.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю: M1 + M2 + ... = 0.
Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Произведение модуля силы F на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки.
|
|
|

Билет 8.
Кинематика вращательно движения твердого тела. Угловое перемещение, угловая скорость, угловое ускорение. Связь между линейными и угловыми характеристиками. Кинетическая энергия вращательного движения.
+Билет 3.
Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω
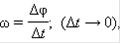

В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.

Вращательно движение твердого тела :
1) вокруг оси - движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси;
2) вокруг точки - движение тела, при котором одна его точка О неподвижна, а все другие движутся по поверхностям сфер с центром в точке О.
Кинетическая энергия вращательного движения.
Кинетическая энергия вращательного движения – энергия тела связанная с его вращением.
|
|
|
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина  зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:
зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

В пределе при Δm → 0 эта сумма переходит в интеграл.
Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

Кинетическая энергия вращательного движения определяется моментом инерции тела относительно оси вращения и его угловой скоростью.
Билет 9.
Дата добавления: 2018-10-26; просмотров: 4598; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
