Задача № 22. Найти наибольший общий делитель двух натуральных чисел

Формулировка. Даны два натуральных числа. Найти их наибольший общий делитель.

Примечание: наибольшим общим делителем (сокращенно пишут НОД) двух натуральных чисел m и n называется наибольший из их общих делителей. Обозначение: НОД(m, n).

Примечание 2: общим делителем двух натуральных чисел называется натуральное число, на которое натуральное число, которое является делителем обоих этих чисел.

Например, найдем НОД(12, 8):

Выпишем все делители числа 12: 1, 2, 3, 4, 6, 12;

Выпишем все делители числа 8: 1, 2, 4, 8;

Выпишем все общие делители чисел 12 и 8: 1, 2, 4. Из них наибольшее число – 4. Это и есть НОД чисел 12 и 8.

Решение. Конечно, при решении мы не будем выписывать делители и выбирать нужный. В принципе, ее можно было бы решить как задачу 14, начав цикл с наименьшего из двух заданных чисел (так как оно тоже может быть НОД, например, НОД(12, 4) = 4). Но мы воспользуемся так называемым алгоритмом Евклида нахождения НОД, который выведен с помощью математических методов. В самом простейшем случае для заданных чисел m и n он выглядит так:

1) Если m неравно n, перейти к шагу 2, в противном случае вывести m и закончить алгоритм;

2) Если m > n, заменить m на m – n, в противном случае заменить n на n – m;

3) Перейти на шаг 1

Как видим, в шаге 2 большее из двух текущих чисел заменяется разностью большего и меньшего.

Приведем пример для чисел 12 и 8:

a. Так как 12 > 8, заменим 12 на 12 – 8 = 4;

b. Так как 8 > 4, заменим 8 на 8 – 4 = 4;

c. 4 = 4, конец.

Не проводя каких-либо рассуждений над алгоритмом и не доказывая его корректности, переведем его описание в более близкую для языка Pascal форму:

Алгоритм на естественном языке:

1) Ввод m и n;

2) Запуск цикла с предусловием m < > n. В цикле:

1. Если m > n, то переменной m присвоить m – n, иначе переменной n присвоить n – m;

3) Вывод m:

Код:

1. program GreatestCommonDiv; 2. 3. var 4. m, n: word; 5. 6. begin 7. readln(m, n); 8. while m <> n do begin 9. if m > n then begin 10. m := m - n 11. end 12. else begin 13. n := n - m 14. end 15. end; 16. writeln(m) 17. end.

Задача № 23. Найти наименьшее общее кратное двух натуральных чисел

Формулировка. Даны два натуральных числа. Найти их наименьшее общее кратное.

Примечание: наименьшим общим кратным двух чисел m и n называется наименьшее натуральное число, которое делится на m и n. Обозначение: НОК(m, n)

Решение. Из теории чисел известно, что НОК(m, n) связан с НОД(m, n) следующим образом:

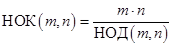
Следовательно, для нахождения ответа нам нужно лишь использовать предыдущую задачу нахождения НОД двух чисел m и n:

while m <> n do begin

if m > n then begin

m := m - n

end

else begin

n := n - m

end

end;

Так как исходные переменные будут испорчены в процессе работы алгоритма Евклида, нам нужно вычислить их произведение до входа в описанный выше цикл и присвоить это произведение переменной prod (от англ. product – «произведение»):

prod := m * n;

После этого нам остается вывести на экран результат арифметического выражения в правой части нашей формулы. В качестве самого НОД будет использоваться переменная m:

writeln(prod div m);

Кстати, деление в формуле будет целочисленным (через div) именно потому, что если два числа делятся на некоторое число, то и их произведение также делится на него.

Код:

1. program LeastCommonMult; 2. 3. var 4. m, n, prod: word; 5. 6. begin 7. readln(m, n); 8. prod := m * n; 9. while m <> n do begin 10. if m > n then begin 11. m := m - n 12. end 13. else begin 14. n := n - m 15. end 16. end; 17. writeln(prod div m) 18. end.

Задача № 24. Вычислить xⁿ

Формулировка. Даны натуральные числа x и n (которое также может быть равно 0). Вычислить xⁿ.

Решение. Для того чтобы решить эту задачу, вспомним определение степени с натуральным показателем: запись xⁿ означает, что число x умножено само на себя n раз.

Сразу из определения видно, что здесь заранее известно количество повторений при вычислении результата, так что задача легко решается через цикл for. Выходит, мы копируем исходное число x в некоторую переменную res (от англ. result – «результат»), а затем просто умножаем его на x n раз? Не стоит торопиться с ответом.

Рассмотрим пример: 3⁴ = 3 * 3 * 3 * 3 = 81. Если посмотреть на эту запись, то мы видим, что возведение в четвертую степень как выражение содержит четыре слагаемых, но только три операции, так как мы с первого шага домножаем число 3 на три тройки. Тогда реализация идеи из абзаца выше будет давать число в степени на 1 больше, чем требуется.

Какой можно придумать выход? Например, можно сократить цикл на одну операцию, но что тогда будет при вычислении нулевой степени? Как известно, любое число в нулевой степени дает 1, а здесь при вводе в качестве n нуля приведет к тому, что не будет осуществлен вход в цикл (так как не существует целочисленного отрезка от 1 до 0) и в итоге на выход так и пойдет исходное число x.

А что, если изменить схему умножения так: 3⁴ = 1 * 3 * 3 * 3 * 3 = 81? Так мы можем сравнять показатель степени и число требуемых операций, да и с нулевой степенью все становится просто, так как при вводе в качестве n нуля не будет осуществляться вход в цикл и на выход в программе пойдет число 1!

Теперь алгоритм на естественном языке:

1) Ввод x и n;

2) Присваивание переменной res числа 1;

3) Запуск цикла, при котором i изменяется от 1до n. В цикле:

1. Присваиваем переменной res значение res * x;

4) Вывод переменной res.

Код:

1. program Exponentiation; 2. 3. var 4. x, n, i, res: word; 5. 6. begin 7. readln(x, n); 8. res := 1; 9. for i := 1 to n do begin 10. res := res * x 11. end; 12. writeln(res) 13. end.

Кстати, стоит понимать, что объявление переменной res при использовании типа word достаточно условно, так как этот тип принимает значения от 0 до 65535, что на единицу меньше числа 256²_,хотя вводить в программу можно числа, предполагающие возведение в более высокую степень. Так как в условии задачи не сказано ничего о том, в каком числовом промежутке по x и n она должна выдавать корректный ответ, оставим это в таком виде, достаточном для проверки приложения на работоспособность.

Задача № 25. Вычислить xⁿ по алгоритму быстрого возведения в степень

Формулировка. Даны натуральные числа x и n. Вычислить xⁿ, используя алгоритм быстрого возведения в степень:

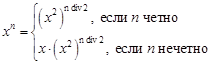
Решение. Разберем этот пока неясный алгоритм, представленный в нашей задаче лишь единственной формулой. Легко понять, что указанное равенство имеет место: например, 3⁴ = 3⁴^{div 2} = (3²)² = 9² = 81. Другой пример: 4⁵ = 4 * (4²)⁵^{div 2}= 4 * (4²)² = 4 * 16² = 4 * 256 = 1024. Причем если выражение со степенью нельзя в один шаг преобразовать таким образом, то необходимо продолжить преобразование выражения вплоть до получения конечного ответа. Однако как теперь реализовать эту схему?

Рассмотрим пример немного сложнее. Вычислим 4⁷ = 4 * (4²)³ = 4 * (16)³ = 4 * 16 * (16²)¹ = 4 * 16 * 256 = 16384. Стоит обратить внимание на то, что на каждом шаге при вычислении изменяется только единственное обрабатывающееся число, а остальные множители выносятся однократно и необходимы только для получения ответа в последнем действии.

Чтобы исключить их из рассмотрения, при нечетном текущем числе n мы будем домножать на них некоторую промежуточную переменную r, поначалу равную 1 (кстати, нечетность числа в Pascal определяет функция odd), затем (уже независимо от условий) возведем в квадрат текущее x и разделим n на 2 с отбрасыванием остатка. При повторении этих действий на некотором шаге n обязательно станет равным 1. Это происходит потому, что деление любого нечетного числа a на 2 с отбрасыванием остатка равносильно делению на двойку числа ( a – 1), которое является четным, и при делении, двигаясь по цепочке четных чисел, мы всегда придем к единице. Условие n = 1 и будет окончанием цикла с предусловием. По выходе из цикла необходимо будет в качестве ответа вывести последнее значение x, умноженное на r.

Теперь алгоритм на естественном языке:

1) Ввод x и n;

2) Присваивание переменной r числа 1;

5) Запуск цикла с предусловием n < > 1. В цикле:

1. Если n нечетно, домножаем r на x;

2. Переменной x присваиваем значение x * x;

3. Переменной n присваиваем результат от деления этой переменной на 2 с отбрасыванием остатка;

3) Вывод выражения x * r.

Код:

1. program FastExponentiation; 2. 3. var 4. x, n, r: word; 5. 6. begin 7. readln(x, n); 8. r := 1; 9. while n <> 1 do begin 10. if odd(n) then r := r * x; 11. x := x * x; 12. n := n div 2 13. end; 14. writeln(x * r) 15. end.

Из анализа данного алгоритма известно, что его асимптотическая сложность порядка O(log₂n).

Дата добавления: 2018-10-25; просмотров: 1080; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!