Марковский процесс с дискретным временем
Основные понятия Марковских процессов
Марковские случайные процессы названы по имени выдающегося русского математика А.А. Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать “динамикой вероятностей”. В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория Марковских процессов и ее приложения широко применяются в самых различных областях таких наук, как механика, физика, химия и др.
Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений особое внимание Марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.
Несмотря на указанную выше простоту и наглядность, практическое применение теории Марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров.
Как указывалось, Марковские случайные процессы относятся к частным случаям случайных процессов (СП). В свою очередь, случайные процессы основаны на понятии случайной функции (СФ).
Случайной функцией называется функция, значение которой при любом значении аргумента является случайной величиной (СВ). По- иному, СФ можно назвать функцию, которая при каждом испытании принимает какой-либо заранее неизвестный вид.
|
|
|
Такими примерами СФ являются: колебания напряжения в электрической цепи, скорость движения автомобиля на участке дороги с ограничением скорости, шероховатость поверхности детали на определенном участке и т.д.
Как правило, считают, что если аргументом СФ является время, то такой процесс называют случайным. Существует и другое, более близкое к теории принятия решений, определение случайных процессов. При этом под случайным процессом понимают процесс случайного изменения состояний какой-либо физической или технической системы по времени или какому-либо другому аргументу.
Нетрудно заметить, что если обозначить состояние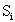 
и изобразить зависимость 
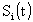, то такая зависимость и будет случайной функцией.
Случайные процессы классифицируются по видам состояний 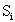и аргументу t. При этом случайные процессы могут быть с дискретными или непрерывными состояниями или временем.
Кроме указанных выше примеров классификации случайных процессов существует еще одно важное свойство. Это свойство описывает вероятностную связь между состояниями случайных процессов. Так, например, если в случайном процессе вероятность перехода системы в каждое последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия.
|
|
|
Отметим, во-первых, что случайный процесс с дискретными состояниями и временем называется случайной последовательностью.
Если случайная последовательность обладает Марковским свойством, то она называется цепью Маркова.
С другой стороны, если в случайном процессе состояния дискретны, время непрерывно и свойство последействия сохраняется, то такой случайный процесс называется Марковским процессом с непрерывным временем.
Марковский случайный процесс называется однородным, если переходные вероятности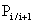 
остаются постоянными в ходе процесса.
Цепь Маркова считается заданной, если заданы два условия.
1. Имеется совокупность переходных вероятностей в виде матрицы:
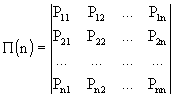. (2)
2. Имеется вектор начальных вероятностей
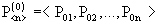, ….. (3)
описывающий начальное состояние системы.
Кроме матричной формы модель Марковской цепи может быть представлена в виде ориентированного взвешенного графа (рис. 1).
|
|
|
Рис. 1 Ориентированный взвешенный граф
Множество состояний системы Марковской цепи, определенным образом классифицируется с учетом дальнейшего поведения системы.
1. Невозвратное множество (рис. 2).
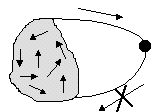
Рис.2. Невозвратное множество
В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.
2. Возвратное множество (рис. 3).
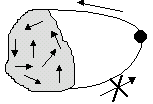
Рис. 3. Возвратное множество
В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.
3. Эргодическое множество (рис. 4).
Рис. 4. Эргодическое множество
В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.
4. Поглощающее множество (рис. 5)
Рис. 5. Поглощающее множество
При попадании системы в это множество процесс заканчивается.
В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие Марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений, о чем будет сказано впоследствии.
|
|
|
Основным признаком дискретной Марковской цепи (ДМЦ) является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими.
Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний Марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество. В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (циклов) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают.
Марковский процесс с дискретным временем
Итак, модель Марковского процесса представим в виде графа, в котором состояния (вершины) связаны между собой связями (переходами из i-го состояния в j-е состояние), см. рис. 1.
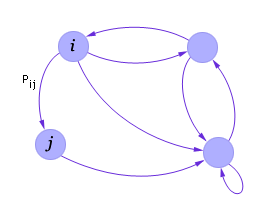
Рис. 2.1. Пример графа переходов
Каждый переход характеризуется вероятностью перехода Pij. Вероятность Pij показывает, как часто после попадания в i-е состояние осуществляется затем переход в j-е состояние. Конечно, такие переходы происходят случайно, но если измерить частоту переходов за достаточно большое время, то окажется, что эта частота будет совпадать с заданной вероятностью перехода.
Ясно, что у каждого состояния сумма вероятностей всех переходов (исходящих стрелок) из него в другие состояния должна быть всегда равна 1 .
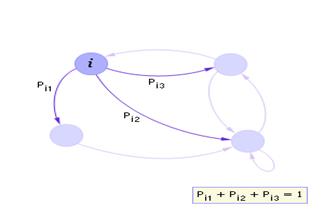
Рис. 2.2. Фрагмент графа переходов (переходы из i-го состояния являются полной группой случайных событий)
Реализация Марковского процесса (процесс его моделирования) представляет собой вычисление последовательности (цепи) переходов из состояния в состояние (см. рис.2.3.). Цепь является случайной последовательностью и может иметь также и другие варианты реализации.
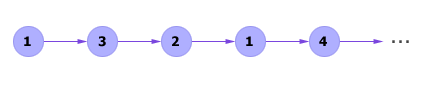
Рис. 2.3.. Пример марковской цепи, смоделированной по марковскому графу, изображенному на рис. 2.2.
Математический аппарат дискретных Марковских цепей
Основным математическим соотношением для ДМЦ является уравнение, с помощью которого определяется состояние системы на любом ее k-м шаге. Это уравнение имеет вид:
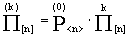(4)
и называется уравнением Колмогорова-Чепмена.
Уравнение Колмогорова-Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний Марковского случайного процесса на любом шаге (этапе) при наличии информации о предшествующих состояниях.
Дата добавления: 2018-10-26; просмотров: 418; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!