Постановка задачи многомерной оптимизации
Пусть f(x) = f(x1, x2, … ,xn) – действительная функция n переменных, определенная на множестве X Ì Rn. Точка x* Î X называется точкой локального минимума f(x) на множестве X, если существует такая e-окрестность этой точки, что для всех x из этой окрестности, т. е., если || x - x*|| < e, выполняется условие f(x*) £ f(x). Если выполняется условие f(x*) < f(x), то x* называется точкой строгого локального минимума. У функции может быть несколько локальных минимумов. Точка x*Î X называется точкой глобального минимума f(x) на множестве X, если для всех x Î X выполняется условие f(x*) £ f(x). Значение функции f(x*) называется минимальным значением f(x) на множестве X, Для нахождения глобального минимума необходимо найти все локальные минимумы и выбрать наименьшее значение. В дальнейшем будем рассматривать задачу нахождения локального минимума.
Необходимые сведения из курса математического анализа
Множество точек, для которых функция принимает постоянное значение f(x) = c, называется поверхностью уровня. Если число переменных n = 2, это множество называют линией уровня. На рис 2.1 показано, как получаются линии уровня для функции двух переменных. Функция f(x1, x2) задает в трехмерном пространстве некоторую поверхность u = f(x1, x2), низшая точка которой и дает решение задачи минимизации. Для того, чтобы изобразить рельеф этой поверхности, проведем несколько равноотстоящих плоскостей u = const. Проекции на плоскость (x1 x2) линий пересечения этих плоскостей с поверхностью u = f(x1, x2) и дают линии уровня.
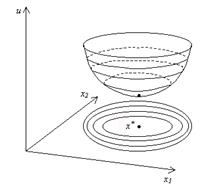
Рис. 2.1
Вектор из первых частных производных
g(x) = f '(x) = 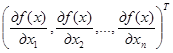
называется градиентом. Если в точке x градиент не равен нулю, то он перпендикулярен проходящей через эту точку поверхности уровня и указывает направление наискорейшего возрастания функции. Вектор – g(x) называется антиградиентом и указывает направление наискорейшего убывания функции (рис. 2.2).
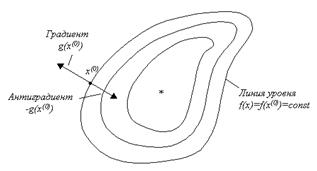
Рис. 2.2
Точка x, для которой градиент равен нулю, т.е.
f '(x) = 0, (2.11)
называется стационарной точкой. Условие (2.11) является необходимым условием того, чтобы точка x была точкой локального минимума дифференцируемой функции f(x).
Равенство (2.11) представляет собой систему n нелинейных уравнений с неизвестными x1, x2, …, xn, которая в развернутом виде выглядит так:
 = 0,
= 0,
……………………. (2.12)
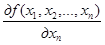 = 0
= 0
Достаточным условием того, чтобы стационарная точка x была точкой локального минимума, является положительная определенность (см. п. 2.1) матрицы
G(x) = f "(x) = 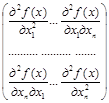 , (2.13)
, (2.13)
составленной из вторых частных производных функции f(x). Матрица (2.13) называется матрицей Гессе.
Важную роль в задачах безусловной оптимизации играют квадратичные функции, которые имеют следующий вид:
f(x) = 
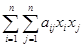 +
+ 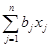 + с. (2.14)
+ с. (2.14)
Используя матричные обозначения, квадратичную функцию f(x) можно записать так:
f(x) =  (Ax , x) + (b, x) + c, (2.15)
(Ax , x) + (b, x) + c, (2.15)
где A – симметричная положительно определенная матрица, b – вектор-столбец коэффициентов bj.
Вычислим градиент и матрицу Гессе для квадратичной функции (2.15). Продифференцировав f(x) по xk, получим
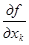 =
= 
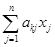 +
+ 
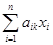 + bk.
+ bk.
Так как aik = aki в силу симметрии матрицы A, получим формулу
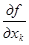 =
= 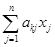 + bk. (2.16)
+ bk. (2.16)
Матричная форма (2.16) имеет вид:
f '(x) = Ax + b . (2.17)
Дифференцируя обе части равенства (2.16) по xi, получим
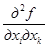 = aik.
= aik.
Это означает, что для квадратичной функции (2.14) матрица Гессе не зависит от x и равна A.
Пример 2.1.
Дана квадратичная функция
f(x) = 2x 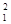 – 2x1x2 + 3x1x3 +x
– 2x1x2 + 3x1x3 +x 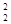 – 2x2x3 + 4x
– 2x2x3 + 4x 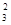 + x1 – x2 + 3x3 +5.
+ x1 – x2 + 3x3 +5.
Запишем матрицу A, вектор b и коэффициент c:
4 -2 3 1
A = -2 2 -2 , b = -1 , c = 5.
3 -2 8 3
Найдем первые производные f(x):
 = 4x1–2x2 +3x3+1,
= 4x1–2x2 +3x3+1,  = –2x1+2x2 – 2x3 – 1,
= –2x1+2x2 – 2x3 – 1,  = 3x1–2x2 +8x3 + 3.
= 3x1–2x2 +8x3 + 3.
Найдем вторые производные f(x):
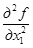 = 4,
= 4, 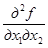 =
=  = –2,
= –2, 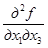 =
= 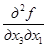 = 3,
= 3, 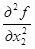 = 2,
= 2,  =
= 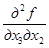 = –2,
= –2, 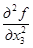 = 8.
= 8.
Легко убедиться, что матрица Гессе равна A .
Пример 2.2.
f(x) = sinx1 + е 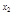 + x1x2.
+ x1x2.
Найдем первые производные f(x):
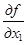 = cosx1 +x2,
= cosx1 +x2,  = е
= е 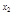 + x1.
+ x1.
Найдем вторые производные f(x):
 = – sinx1,
= – sinx1, 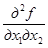 =
=  = 1,
= 1, 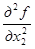 = е
= е 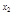 .
.
Матрица Гессе равна
– sinx1 1
1 е 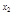 .
.
Методы спуска
Методы спуска – группа методов, широко применяющихся для решения задачи минимизации функции многих переменных f(x) = f(x1, x2, … xn). Основная идея методов спуска состоит в построении минимизирующей последовательности {x(m)}, m = 0, 1, 2, … по алгоритму:
x(m+1) = x(m) + a(m)p(m), (2.18)
где x(m) = (x  , x
, x 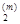 , … , x
, … , x 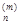 ) – m -оеприближение к точке минимума, p(m) – ненулевой вектор, называемый направлением спуска, a(m) – положительное число, называемое шагом спуска. Различие конкретных методов спуска состоит в способе выбора p(m), a(m).
) – m -оеприближение к точке минимума, p(m) – ненулевой вектор, называемый направлением спуска, a(m) – положительное число, называемое шагом спуска. Различие конкретных методов спуска состоит в способе выбора p(m), a(m).
Опишем общую схему методов спуска. Пусть x(m) = (x  , x
, x 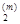 , … , x
, … , x 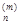 ) –приближение к точке минимума, полученное в результате m -ой итерации.
) –приближение к точке минимума, полученное в результате m -ой итерации.
1. В точке x(m) находят направление спуска p(m) из условия, чтобы при всех достаточно малых a выполнялось неравенство
f (x(m) + a p(m)) < f(x(m)), (2.19)
т.е. значение функции уменьшалось.
2. Вычисляют шаг спуска a(m), так, чтобы выполнялось неравенство
f (x(m) + a(m)p(m)) < f(x(m)),
3. За очередное приближение к точке минимума берут
x(m+1) = x(m) + a(m)p(m). (2.20)
4. Проверяют выполнение критерия окончания итераций. Если критерий выполняется, то итерации прекращают и полагают x * » x(m+1). В противном случае итерации продолжаются.
На практике часто используют следующие критерии окончания итераций:
||x(m+1) – x(m)|| < e, (2.21)
|f(x(m+1)) – f(x(m))| < e, (2.22)
||f '(x(m))|| < e, (2.23)
где e – заданное положительное число (допустимая погрешность).
Последовательность точек x(0), x(1), …, x(m), …называют траекторией спуска.
Дата добавления: 2018-09-23; просмотров: 741; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
