Графический метод решения игр

МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР

В СМЕШАННЫХ СТРАТЕГИЯХ

Постановка вопроса

Если игра n×m не имеет седловой точки, то нахождение решения вообще довольно трудная задача, особенно при больших n и m.

Иногда эту задачу удается упростить, предварительно уменьшив число стратегий путем вычеркивания некоторых излишних.

Излишние стратегии бывают: а) дублирующие и б) заведомо невыгодные.

Рассмотрим, например, игру с матрицей:

В А	В₁	В₂	В₃	В₄
А₁	1	2	4	3
А₂	0	2	3	2
А₃	1	2	4	3
А₄	4	3	1	0

Нетрудно убедиться, что стратегия A₃ в точности повторяет ("дублирует") стратегию A₁, поэтому любую из этих двух стратегий можно вычеркнуть. Далее, сравнивая почленно строки A₁ и A₂, видим, что каждый элемент строки A₂меньше (или равен) соответствующего элемента строки А₁. Очевидно, что мы никогда не должны пользоваться стратегией А₂, она является заведомо невыгодной. Вычеркивая A₃ и A₂, приводим матрицу к более простому виду:

В А	В₁	В₂	В₃	В₄
А₁	1	2	4	3
А₄	4	3	1	0

Далее замечаем, что для противника стратегия В3 заведомо невыгодна; вычеркивая ее, приводим матрицу к окончательному виду :

В А	В₁	В₂	В₄
А₁	1	2	3
А₄	4	3	0

Таким образом, игра 4×4 вычеркиванием дублирующих и заведомо невыгодных стратегий сведена к игре 2×3.

Процедура вычеркивания дублирующих и заведомо невыгодных стратегий всегда должна предшествовать решению игры.

Игры 2×2 и 2×m являются наиболее простыми случаями конечных игр, которые всегда можно решить элементарными способами.

3.2. Аналитический метод решения игры 2×2, 2×m и n×2

Пусть игра 2×2 задана платежной матрицей

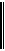
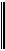а₁₁ а₁₂

А=

а₂₁ а₂₂

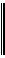
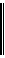Пусть седловой точки нет и, следовательно, нижняя цена игры не равна верхней: α≠β. Требуется найти оптимальную смешанную стратегию игрока A

A₁ A₂

S_a* =

p*₁ p*₂

Она отличается тем свойством, что, каковы бы ни были действия противника (если только он не выходит за пределы своих "полезных" (активных) стратегий), выигрыш будет равен цене игры n. В игре 2×2 обе стратегии противника являются "полезными", - иначе игра имела бы решение в области чистых стратегий (седловую точку). Значит, если мы придерживаемся своей оптимальной стратегии S*_a, то противник может пользоваться любой из своих чистых стратегий B₁, В₂, не изменяя среднего выигрыша n.

То есть, если игрок В использует чистую стратегию B₁ (это соответствует 1-му столбцу платежной матрицы), выигрыш игрока A, применяющего смешанную стратегию, равен цене игры n: a₁₁·p₁* + a₂₁·p₂* = n.

Тот же средний выигрыш получает игрок A, если 2-й игрок применяет стратегию B₂, т.е. a₁₂·p*₁ + a₂₂·p*₂ = n. Учитывая, что p₁* + p₂* = 1, получаем систему уравнений для определения оптимальной стратегии S*_a и цены игры n:

a₁₁·p*₁ + a₂₁·p*₂ = n (3.1)

a₁₂·p*₁ + a₂₂·p*₂ = n

p*₁ + p*₂ = 1

Решая эту систему, получим оптимальную стратегию

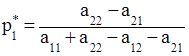(3.2)

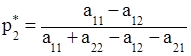
и цену игры

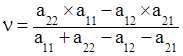(3.3)

Применяя теорему об активных стратегиях при отыскании S*_b - оптимальной стратегии игрока B, получаем, что при любой чистой стратегии игрока A (A₁ или A₂) средний проигрыш игрока B равен цене игры n, т.е.

a₁₁·q*₁+ a₁₂·q*₂ = n (3.4)

a₂₁·q*₁ + a₂₂·q*₂ = n

q*₁ + q*₂ = 1

Тогда оптимальная стратегия S*_b (q*₁, q*₂) определяется формулами:

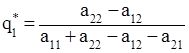(3.5)

Графический метод решения игр

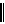Решение игры 2×2 допускает наглядную геометрическую интерпретацию. Пусть игра задана матрицей A= а_ij , i,j=1,2, приведенной ниже.

В А	В₁	В₂
А₁	a₁₁	a₁₂
А₂	a₂₁	a₂₂

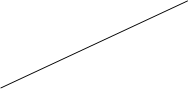
Возьмем участок оси абсцисс длиной 1 (как сумма вероятностей р₁+р₂=1) -рис. 3.1. Левый конец участка (точка с абсциссой х=0) будет изображать стратегию A₁, правый конец участка (х=1)- стратегию A₂. Проведем через точки A₁ и A₂ два перпендикуляра к оси абсцисс: ось I-I и ось II-II. На оси I-I будем откладывать выигрыши при стратегии А1, на оси II-II - выигрыши при стратегии A₂. Рассмотрим стратегию противника В₁; она дает две точки на осях I-I и II-II c ординатами, соответственно, a₁₁ и а₂₁. Проведем через эти точки прямую В₁-В₁.

Очевидно, если мы будем применять смешанную стратегию

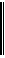
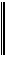A₁ A₂

S_a =

p₁ p₂

а игрок В - чистую стратегию B₁, то наш средний выигрыш, равный а₁₁·р₁ + а₂₁·р₂, изобразится точкой М на прямой В₁-В₁; абсцисса этой точки равна р₂. Прямую В₁-В₁, изображающую выигрыш при стратегии В₁, условно будем называть “стратегией В₁”.

Очевидно, точно таким же способом может быть построена и стратегия В₂ (рис. 3.2).

I II I II

а₁₂

В₁

B₁ B₂

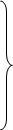
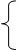
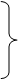
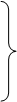
M N

В₂

a₂₁ a₂₁

а₁₁

B₁ n a₂₂

a₁₁ p₂p₁ p₂ p₁

0 (A₁) 1 (A₂) 0 (A₁) 1 (A₂) I II I II

Рис. 3.1. Рис. 3.2.

Нам нужно найти оптимальную стратегию S*_a, т.е. такую, для которой минимальный выигрыш (при любом поведении В) обращался бы в максимум. Для этого построим нижнюю границу выигрыша при стратегиях В₁, В₂, то есть, ломаную В₁-N-В₂, отмеченную на рис. 3.2 жирной линией. Эта нижняя граница будет выражать минимальный выигрыш игрока А при любых смешанных его стратегиях; точка N, в которой этот минимальный выигрыш достигает максимума, и определяет решение и цену игры. Нетрудно убедиться, что ордината точки N есть цена игры n, а ее абсцисса равна р*₂ - частоте применения стратегии A₂ в оптимальной смешанной стратегии S*_a.

Геометрическая интерпретация дает возможность представить наглядно также нижнюю и верхнюю цену игры.

В нашем случае решение игры определялось точкой пересечения стратегий. Однако, это не всегда будет так; на рис. 3.3 показан случай, когда, несмотря на наличие пересечения стратегий, решение дает для обоих игроков чистые стратегии (А₂ и В₂), а цена игры n= а₂₂.

В данном случае матрица имеет седловую точку, и стратегия А₁ является заведомо невыгодной, т.к. при любой чистой стратегии противника она дает меньший выигрыш, чем А₂.

В₂

а₂₁

а₂₂

а₁₂

В₁

I II

В₂

ν =a₂₂

В₁

В₂

В₁

а₂₁

а₁₁

В₁

а₁₁

X X

0 (A₁) 1 (A₂) 0 (A₁) 1 (A₂)

I II I II

Рис. 3.3. Рис. 3.4

В случае, когда заведомо невыгодная стратегия имеется у противника, геометрическая интерпретация имеет вид, представленный на рис.3.4. В данном случае нижняя граница выигрыша совпадает со стратегией В₁; стратегия В₂ для противника является заведомо невыгодной.

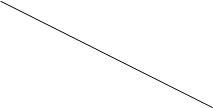
Пусть мы располагаем двумя стратегиями А₁, А₂, а противник - m стратегиями: В₁, В₂, ..., В_m. Матрица а_ij задана; она состоит из двух строк и m столбцов. Аналогично случаю двух стратегий, дадим задаче геометрическую интерпретацию; m стратегий противника изобразятся m прямыми (рис. 3.5).

А₃

А₁

I II I II

А₄

А₁

B₂ B₁

B₃

А₂

А₄

B₃ B₄

А₃

B₄ B₂

А₂

B₁ ν ν

0 (A₁) p₂ p₁1 (A₂) 0 (В₁) q₂ q₁1 (B₂)

I II I II

Рис. 3.5. Рис. 3.6.

Строим нижнюю границу выигрыша (ломаную В₁MNВ₂) и находим на ней точку N с максимальной ординатой. Эта точка дает решение игры (стратегию)

A₁ A₂

S*_a =

р*₁ p*₂

координата точки N равна цене игры n, а абсцисса равна частоте р*₂ стратегии А₂. В данном случае оптимальная стратегия противника получается применением смеси двух “полезных” (активных) стратегий: В₂ и В₄, пересекающихся в точке N. Стратегия В₃ является заведомо невыгодной, а стратегия В₁ - невыгодной при оптимальной стратегии S*_a.

Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих "полезных" стратегий не пользовался В, однако, он изменится, если В перейдет к стратегиям В₁ или В₃.

Пользуясь геометрической интерпретацией, можно дать простой способ решения любой игры 2´m. Непосредственно по чертежу находим пару "полезных" стратегий противника В_j и В_k, пересекающихся в точке N (если в точке N пересекаются более двух стратегий, берем любые две из них). Мы знаем, что, если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои "полезные" стратегии, следовательно

a₁_j·p₁ + a₂_j·p₂ = n a₁_k·p₁ + a₂_k·p₂ = n

Из этих уравнений и условия р₂ =1 - р₁ находим р₁, р₂ и цену игры. Зная цену игры, можно определить оптимальную стратегию игрока В:

B_j B_k

S*_b =

q_j q_k

Для этого решается, например, уравнение: q_j·a_1j + q_k·a_1k = n, где q_j + q_k = 1.

В случае, когда мы располагаем n стратегиями, а противник - всего двумя, задача решается совершенно аналогичным способом: заменяя знак выигрыша на обратный, можно превратить игрока А из "выигрывающего" в "проигрывающего". Можно решить задачу и без перемены знака выигрыша; тогда задача решается непосредственно для В, но строится не нижняя, а верхняя граница выигрыша (рис. 3.6). На границе ищется точка N с минимальной ординатой, которая и есть цена игры n.

Дата добавления: 2018-09-22; просмотров: 461; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!