Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
Дифференциальные уравнения высших порядков, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью подстановки данное ДУ сводится к уравнению более низкого порядка.
Рассмотрим три типа уравнений, допускающих понижение порядка.
I.  .
.
Это уравнение интегрируется непосредственно n раз. При каждом интегрировании порядок уравнения понижается на единицу, и появляется произвольная постоянная.
Пример 1. Решить уравнение  .
.
Решение:  ;
;
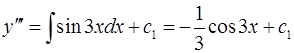 ;
;
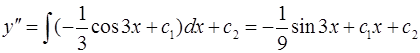 ;
;
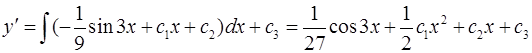 ;
;
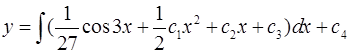 ;
;
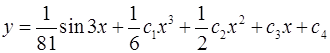 .
.
Ответ: 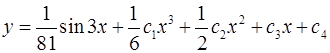 .
.
II. Если дифференциальное уравнение порядка 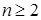 имеет вид
имеет вид 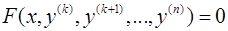 , т.е. не содержит искомой функции и ее производных до порядка
, т.е. не содержит искомой функции и ее производных до порядка  включительно, то порядок уравнения может быть понижен с помощью подстановки
включительно, то порядок уравнения может быть понижен с помощью подстановки 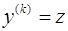 .
.
Пример.2. Решить уравнение 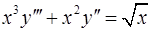 .
.
Решение: уравнение не содержит y и y ¢, поэтому порядок уравнения понижается до первого с помощью подстановки 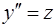 (при этом
(при этом 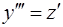 ).
).
Уравнение принимает вид 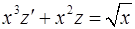 – линейное уравнение первого порядка. Решая его методом подстановки или методом вариации, находим
– линейное уравнение первого порядка. Решая его методом подстановки или методом вариации, находим 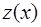 .
.
Возвратимся к исходной переменной: 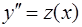 . Два раза проинтегрировав последнее выражение, найдем общее решение исходного уравнения:
. Два раза проинтегрировав последнее выражение, найдем общее решение исходного уравнения:
III. Если уравнение не содержит независимой переменной, т.е. имеет вид 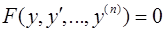 , то порядок уравнения понижается на единицу с помощью замены
, то порядок уравнения понижается на единицу с помощью замены 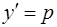 . При этом y рассматривается как новая независимая переменная, а p – как новая неизвестная функция, производные
. При этом y рассматривается как новая независимая переменная, а p – как новая неизвестная функция, производные 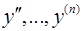 выражаются через p и производные функции p по y.
выражаются через p и производные функции p по y.
|
|
|
Выразим, например, 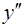 . Поскольку
. Поскольку 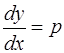 , то
, то
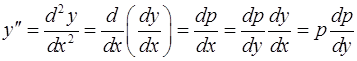 .
.
Аналогично выражается 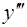 :
:  .
.
Пример 3. Найти решение уравнения 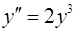 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
, 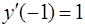 .
.
Решение: примем y за новую независимую переменную, а 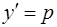 – за новую неизвестную функцию. Тогда
– за новую неизвестную функцию. Тогда 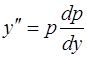 , и данное уравнение в новых переменных примет вид
, и данное уравнение в новых переменных примет вид
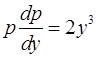 – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
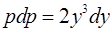 ,
,
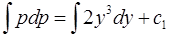
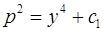 .
.
Произвольную константу 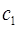 определяем, используя начальные условия
определяем, используя начальные условия  ,
, 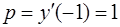 . Подставляя эти условия в найденное решение, получаем
. Подставляя эти условия в найденное решение, получаем 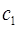 =0. Поэтому
=0. Поэтому 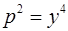 , или
, или 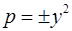 , т.е.
, т.е. 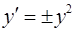 .
.
Данным начальным условиям может удовлетворять только решение уравнения 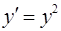 (в случае
(в случае 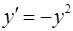 при
при 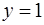
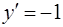 )
)
Общее решение уравнения 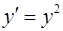 дается формулой
дается формулой 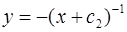 . Из условия
. Из условия  следует, что
следует, что  , и искомым решением будет
, и искомым решением будет 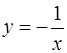 .
.
Ответ: 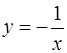 .
.
Линейные дифференциальные уравнения высших порядков
Линейным дифференциальным уравнением n-го порядканазывается уравнение вида
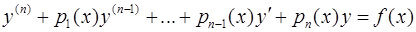 . .
| (1) |
Далее будем предполагать, что коэффициенты 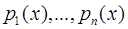 и
и 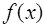 определены и непрерывны при
определены и непрерывны при  .
.
Если 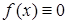 на интервале
на интервале 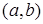 , то уравнение называется однородным, в противном случае – неоднородным.
, то уравнение называется однородным, в противном случае – неоднородным.
Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения n-го порядка):общее решение линейного неоднородного дифференциального уравнения n-го порядка представляется в виде суммы общего решения соответствующего однородного ДУ и частного решения неоднородного дифференциального уравнения: 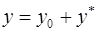 .
.
|
|
|
Теорема (о структуре общего решения линейного однородного дифференциального уравнения n-го порядка): общее решение линейного однородного дифференциального уравнения n-го порядка представляется в виде линейной комбинации n линейно независимых частных решений этого уравнения:
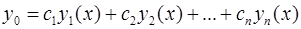
где  – произвольные постоянные,
– произвольные постоянные, 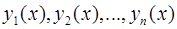 – частные линейно независимые решенияоднородного уравнения, т.е. такие решения, для которых составленный из них определитель Вронского (вронскиан) не равен нулю:
– частные линейно независимые решенияоднородного уравнения, т.е. такие решения, для которых составленный из них определитель Вронского (вронскиан) не равен нулю:
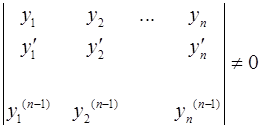 .
.
n линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка образуют фундаментальную систему решенийэтого уравнения.
Если известна фундаментальная система решений однородного уравнения, то согласно методу Лагранжа (методу вариации произвольных постоянных), решение соответствующего неоднородного уравнения можно найти в виде
 ,
,
где неизвестные функции  определяются из системы уравнений
определяются из системы уравнений
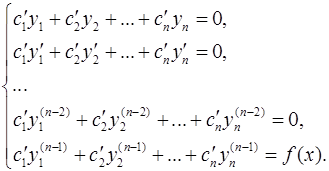
В частности, для уравнения второго порядка 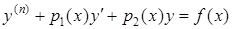 эта система принимает вид
эта система принимает вид
|
|
|
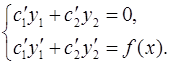
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
Линейным дифференциальным уравнением n-го порядкас постоянными коэффициентами называется уравнение вида
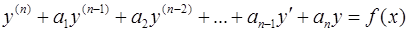 , ,
| (2) |
где 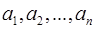 – некоторые числа.
– некоторые числа.
Построение фундаментальной системы решений однородного линейного уравнения с постоянными коэффициентами.
Однородное линейное уравнение с постоянными коэффициентами
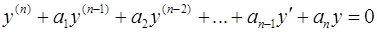 . .
| (3) |
имеет фундаментальную систему решений  , определенную при всех x, структура которой зависит от вида корней характеристического уравнения
, определенную при всех x, структура которой зависит от вида корней характеристического уравнения
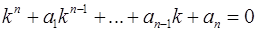 . .
| (4) |
Каждому действительному простому корню  характеристического уравнения (13) соответствует решение
характеристического уравнения (13) соответствует решение 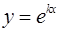 , входящее в фундаментальную систему.
, входящее в фундаментальную систему.
Если уравнение (13) имеет простой комплексный корень 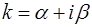 , то сопряженное число
, то сопряженное число 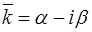 тоже будет корнем уравнения, и корням
тоже будет корнем уравнения, и корням 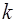 ,
, 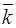 соответствуют два линейно-независимых частных решения
соответствуют два линейно-независимых частных решения 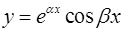 и
и  , входящих в фундаментальную систему.
, входящих в фундаментальную систему.
Действительному корню 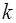 уравнения (13), имеющему кратность p , соответствует p линейно-независимых частных решений
уравнения (13), имеющему кратность p , соответствует p линейно-независимых частных решений 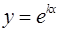 ,
, 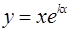 ,
, 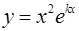 ,...,
,..., 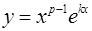 , входящих в фундаментальную систему.
, входящих в фундаментальную систему.
p -кратным комплексно-сопряженным корням 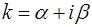 и
и  соответствует 2p линейно-независимых решений вида
соответствует 2p линейно-независимых решений вида
|
|
|
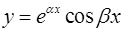 ,
, 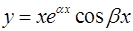 ,
, 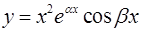 ,...,
,...,  ,
,
 ,
, 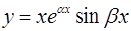 ,
, 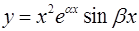 ,...,
,..., 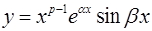 ,
,
входящих в фундаментальную систему.
Таким образом, для того, чтобы найти общее решение линейного однородного уравнения с постоянными коэффициентами, надо найти корни характеристического уравнения, а затем выписать линейно-независимые решения указанного выше вида, соответствующие всем простым и кратным корням уравнения (4). Линейная комбинация этих решений дает общее решение уравнения (3).
Пример 4. Найти общее решение уравнения 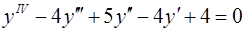 .
.
Решение: общее решение имеет вид 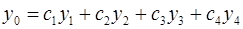
Составим и решим характеристическое уравнение 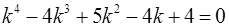 .
.
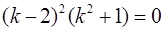 ;
;
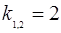 ,
,  .
.
Таким образом, характеристическое уравнение имеет корни: 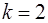 – корень кратности 2, ему отвечают два линейно-независимых решения
– корень кратности 2, ему отвечают два линейно-независимых решения 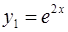 и
и 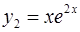 ;
; 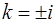 – пара комплексно-сопряженных корней, им соответствуют решения
– пара комплексно-сопряженных корней, им соответствуют решения  и
и  .
.
Общее решение исходного уравнения имеет вид 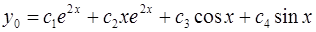 .
.
Ответ: 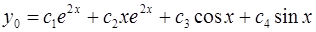 .
.
Пример 5. Решить неоднородное уравнение 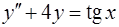 .
.
Решение:
1). Найдем общее решение соответствующего однородного уравнения 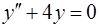 . Характеристическое уравнение
. Характеристическое уравнение 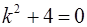 имеет корни
имеет корни 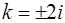 , поэтому
, поэтому 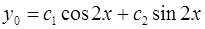 – общее решение однородного уравнения.
– общее решение однородного уравнения.
2). Общее решение исходного уравнения будем искать методом вариации произвольных постоянных в виде  .
.
Функции 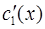 и
и 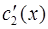 находим из системы
находим из системы
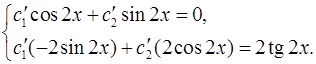
Решая систему, получаем: 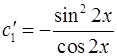 ,
,  .
.
Интегрируя, находим:
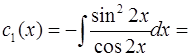
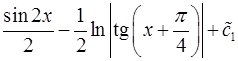 ;
;
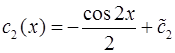 ,
,
где 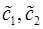 – произвольные постоянные.
– произвольные постоянные.
Общее решение исходного уравнения имеет вид
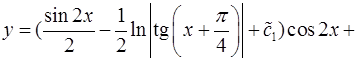
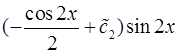 .
.
Упростив это выражение, получим
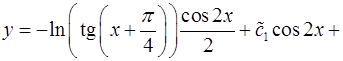
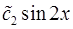 .
.
Ответ: 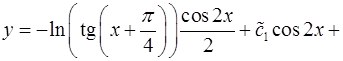
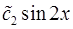 .
.
Дата добавления: 2018-09-20; просмотров: 612; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
