Глава 1. Теорема Шеннона о существовании пропускной способности канала без шума

Стр 1 из 2Следующая ⇒

Nbsp; Ю.Я. АГРАНОВИЧ, С.Л. ПОДВАЛЬНЫЙ, Н.В. КОНЦЕВАЯ, И.Я. НОВИКОВ, В.Л. ХАЦКЕВИЧ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРЕТИЧЕСКОЙ ИНФОРМАТИКИ

Воронеж – 2010

УДК 681
ББК 22.18
М34

Математические основы теоретической информатики: учеб. пособие / Ю.Я. Агранович, С.Л. Подвальный, Н.В. Концевая, И. Я. Новиков, В.Л. Хацкевич. – Воронеж: Изд-во «Институт ИТОУР», 2010. – 100 с.

Ил.:5. Библиогр.:21 назв.

ISBN 978-5-91667-019-6

Данное учебное пособие восполняет пробел, имеющийся в учебной литературе по теоретическим основам информатики. Наряду с подробным обсуждением теоремы К. Шеннона о пропускной способности пособие содержит необходимые сведения об уравнениях в конечных разностях и теории чисел.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по специальности 230101 «Вычислительные машины, комплексы, системы и сети» дисциплине «Информатика». Предназначено для студентов заочной формы обучения и является переработанным изданием учебного пособия «Элементы теоретической информатики» Ю.Я. Аграновича, С.Л. Подвального, И. Я. Новикова, В. Л. Хацкевича.

ISBN 978-5-91667-019-6

Предисловие

Современная учебная литература по теоретической информатике рассчитана, как правило, на людей, имеющих профессиональное математическое образование. К числу таких руководств относятся, например, прекрасные учебники Д. Кнута «Искусство программирования для ЭВМ», «Конкретная математика», однако многолетний опыт преподавания показывает, что студентам инженерных специальностей необходима серьезная предварительная подготовка, после которой можно приступать к изучению указанных выше учебников.

Этот пробел восполняет предлагаемый вводный курс лекций. В нем кроме подробного изложения результатов К. Шеннона по пропускной способности канала без шума и канала с гауссовским белым шумом, излагаются методы решения уравнений в конечных разностях, обсуждаются задача А.А. Маркова и ее обобщение, рассматриваются свойства многоугольных чисел, изложен метод решения уравнения Ферма (Пелля) и близкие вопросы диофантова анализа.

Таким образом, настоящее пособие можно рекомендовать также для первоначального изучения классической теории чисел. Изложение очень подробно и содержит полные доказательства, а также большое количество полностью разобранных конкретных числовых примеров.

Текст лекций сопровождается задачами, среди которых иногда встречаются простые. Решение задач направлено на углубление понимания изучаемого материала. Они могут служить предметом лабораторных работ и самостоятельных исследований студентов.

Главы 5-7, набранные курсивом, предназначены для изучения некоторых специальных разделов информатики.

Авторы благодарны Елене Петровне Федаковой, которая взяла на себя нелёгкий труд компьютерного набора текста этих лекций, а также всем студентам Воронежского государственного технического университета, обучающимся по специальности «Вычислительные машины, комплексы, системы и сети», которые принимали активное участие в решении предложенных задач.

Введение

Информатика первоначально появилась как раздел теории связи. Однако статистический анализ погрешности передачи сообщений сравнительно быстро уступил место теоретико-числовому подходу. Основы такого понимания были заложены К. Шенноном и Н. Винером. По видимому, в целом, это привело к актуализации дискретной математики. По существу в настоящее время информатику можно считать прикладной теорией чисел. Наша небольшая книжка почти полностью посвящена изложению этой дискретной составляющей теоретической информатики.

Изустная форма передачи знания была наиболее плодотворной. Немедленная обратная связь позволяла развиваться учителю и ученикам, делая их соавторами и союзниками, определяющими облик научной школы. По видимому, такая форма обучения была присуща Древнему Египту. Более позднее греческое знание уже в значительной мере тяготело к тексту, к письменной форме передачи информации. Хотя вот интересный парадокс: именно хранитель Александрийской библиотеки Эратосфен (276г. до Р.Х. – 196г. до Р.Х.), известный как автор «решета Эратосфена», наверное, одного из самых перспективных способов изучения свойств целых чисел, мог позволить себе столь свободное, по существу, лекционное отношение к письменному тексту. Возможно, именно как хранитель библиотеки, он, как никто другой, ощущал присутствие египетской формы знания? Лекционная форма передачи знания с многочисленными поясняющими рисунками, терминами, ссылками на различные литературные источники, наиболее важными кусками формулировок, и всё это постоянно варьируется на доске. Как можно совместить такое свободное отношение к тексту, то и дело возникающему на доске, с внутренним смыслом этих лекций, с их семантикой – теоретическая информатика, то есть с изучением способов передачи и хранения информации?

Издание такого курса лекций априори, предполагает неизбежную потерю информации, иногда очень значимой и почти всегда – ключевой. Восполнить естественные в таких случаях пробелы позволяет изучение дополнительной литературы.

По основам статистической теории связи можно рекомендовать следующие издания: А.А. Харкевич «Очерки общей теории связи». М.: ГИТТЛ, 1955, «Борьба с помехами». М.: ГИФМЛ, 1963, Б. П. Латхи «Системы передачи информации». М.: Изд-во «Связь», 1971, В. Денда «Шум как источник информации», М. -Мир, 1993. Список фундаментальных работ в области информатики содержит также библиографический список в конце книги.

Глава 1. Теорема Шеннона о существовании пропускной способности канала без шума

Начнем с нескольких предварительных определений. Объекты, которые мы попытаемся определить, имеют фундаментальный характер и, в сущности, весь наш курс направлен на то, чтобы углубить теоретическое понимание информатики как фундаментальной науки, основанной на результатах комбинаторики, алгебры и теории чисел.

Определение (рабочее). Будем называть информатикой науку о формировании структуры сигналов.

Предположения о существовании:

1. Мы предполагаем, что существует «канал», т.е. среда, в которой распространяются сообщения. «Канал» может иметь качественно различную природу: естественный или искусственный.

Например:

а) ДНК – канал распространения наследственных сообщений – естественный канал;

б) почтовая система – канал распространения письменных сообщений – искусственный канал;

в) полоса частот – канал распространения сообщений закодированных электромагнитными волнами;

г) лекция в Вашей группе – естественный канал распространения сообщений между мной и Вами.

2. Мы предполагаем, что существуют сигналы, т.е. сообщения, имеющие внутреннюю энергию, упорядоченность в совокупности и внутреннюю структуру, определяющую семантику этих сообщений.

Сигналы имеют минимальную продолжительность по времени 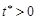. Каждый сигнал имеет продолжительность , где n произвольное натуральное число. Далее естественно установить временной масштаб, так чтобы 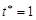(единица времени), что мы и делаем. Это предположение определяет отличие информатики от систем массового обслуживания, где 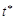, вообще говоря, отсутствует и продолжительность запроса может быть сколь угодно малой, например, ошибочный звонок по телефону.

Обозначим через число допустимых для передачи сигналов длительности Т. Здесь N и Т являются натуральными числами. Таким образом, мы рассматриваем целочисленную функцию от целочисленного аргумента. Получим соотношение для , считая, что сигнал состоит из последовательно передаваемых символов 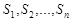(конечный алфавит) длительностей соответственно 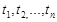(также натуральные числа).

Тогда полное число всех последовательностей передаваемых за время Т равно сумме всех последовательностей заканчивающихся символом , всех последовательностей заканчивающихся символом 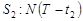и т.д. 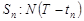, то, верно, такое соотношение:

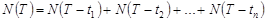. (1.1)

Пример: работа телетайпа, где передаются только точки и тире. В этой системе точка кодируется замыканием линии на 1 единицу времени, тире размыканием на 1 единицу времени.

10 – «точка»,

1110 – «тире»,

000 – «пробел между буквами»,

000000 – «пробел между словами».

Тогда возможные окончания:

S₁: 10 длительность 2 единицы времени,

S₂: 1110 длительность 4 единицы времени,

S₃: 10000 длительность 5 единиц времени (конец передачи буквы, заканчивающийся «точкой»),

S₄: 1110000 длительность 7 единиц времени (конец передачи буквы, заканчивающейся «тире»),

S₅: 10000000 длительность 9 единиц времени (конец слова с точкой в конце),

S₆: 1110000000 длительность 10 единиц времени (конец слова с тире в конце).

Уравнение (1.1) принимает в этом случае вид:

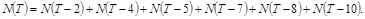(1.1^*)

Соотношение вида (1.1) называется уравнением в конечных разностях. Будем искать решение этого уравнения в виде:

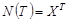. (1.2)

Подставляя (1.2) в (1.1), получим:

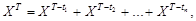
откуда

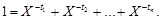(1.3)

Сделаем замену 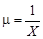, тогда (1.3) примет вид:

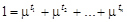. (1.4)

Так как 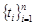– последовательность натуральных чисел, то решение (1.4) сводится к определению вещественных корней многочлена (1.4). Такие корни есть, в самом деле, при μ=0 имеем 1>0, а при μ=1: 1≤n, т.е. по крайней мере, один корень на интервале (0,1] есть.

Рассмотрим сначала самый простой случай: все вещественные корни многочлена (1.4) различны: .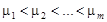

В силу однородности уравнения (1.1), если 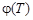– решение, то и 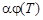– также решение. В силу аддитивности, мы можем складывать решения, и снова получим решение. Таким образом, можно представить найденные решения в виде:

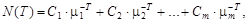(1.5)

где 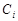– произвольные неотрицательные числа .

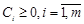В силу предположения (1.3) – 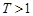, так как в противном случае мы не смогли бы передать и одного сигнала 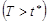. Поэтому справедлива такая верхняя оценка для :

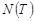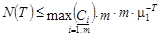. (1.6)

При 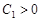, справедлива также нижняя оценка для :

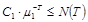Таким образом, мы получим следующую двустороннюю оценку для :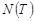

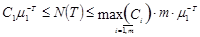. (1.7)

Прологарифмируем теперь (1.7), получим:

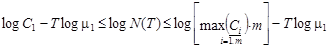Возвращаясь к Х и обозначая 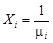, получим, что Х₁ – наибольший вещественный корень уравнения (1.3) и справедлива оценка:

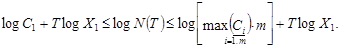(1.8)

Разделим (1.8) на Т, получим:

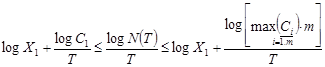. (1.9)

Устремим теперь Т в бесконечность, считая, что длительности сообщений сколь угодно велики, тогда из (1.9) немедленно получим, что:

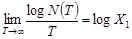. (1.10)

Это фундаментальное соотношение, которое показывает, что существует некоторая характеристика канала относительно заданного конечного алфавита 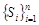. Эта характеристика больше ни от чего не зависит. Клод Шеннон назвал величину 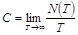– «пропускная способность канала». А мы, тем самым доказали ее существование в самом простом случае.

Для полноты картины рассмотрим теперь случай кратных корней. Для определенности будем считать, что корень Х₁ имеет кратность 2, т.е. многочлен в (1.4) может быть записан так:

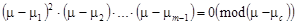
по модулю всех комплексных корней.

В этом случае, кроме решения 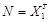, есть еще одно решение (линейно-независимое): .

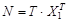В самом деле, будем искать решение уравнения в виде:

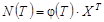. (1.11)

Подставляя в (1.1), получим:

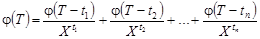. (1.12)

Положим 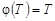, тогда из (12) получим:

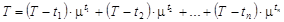. (1.13)

Мы здесь находим формулы для решений. И понятно, что формулы эти мы найдём. И в этот момент может показаться, что мы полностью решили задачу, как это было раньше в курсе дифференциальных уравнений. Осторожно! Это глубокое заблуждение, Мы почти также далеки от полного решения задачи, как и в момент написания исходного уравнения в конечных разностях. В самом деле, как величина Т, так и величина N – целые числа. Но не каждое натуральное число можно подставлять в качестве Т, а только такое, которое может быть представлено в виде суммы длительностей букв алфавита. Таким образом, значения аргумента найденных нами функций вовсе не произвольны, а очень специальны. На самом деле, определение таких значений Т эквивалентно решению исходной задачи. И возникает вопрос, зачем Шеннон это всё делает? Ответ состоит в том, что его, а вслед за ним и нас, интересует асимптотическое поведение решений, а не сами решения. Именно на этом пути Шеннон вводит понятие пропускной способности канала. Это предельное, асимптотическое понятие. К счастью метод уравнений в конечных разностях как будто специально предназначен для получения асимптотик решений. Ну хорошо, а как же быть с точными решениями, спросите Вы. Ведь у нас уже получены окончательные формулы решений. На самом деле, здесь дело обстоит значительно интересней, чем это может показаться с первого взгляда. Вы уже понимаете, что для корректного обращения к этим формулам, надо предварительно решить сложную задачу из теории чисел. Не смотря на значительные усилия таких выдающихся математиков как Эйлер, Лежандр, Лиувилль теория разбиения чисел ещё очень далека от завершения. Для решения указанных задач Эйлер построил теорию производящих функций, так, что есть и другие формальные выражения для решения, а не только полученные нами. В нашем небольшом курсе мы не сможем рассмотреть этот подход.

Мы проведём сейчас рассуждения несколько по-другому, нежели на предыдущей лекции. Дело в том, что на самом деле здесь не может быть положительных кратных корней. Но при этом очень хотелось бы продемонстрировать силу применяемого метода.

Покажем, что на самом деле многочлен (1.4) не имеет положительных кратных корней. В самом деле, если кратный корень есть, то тогда 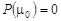и 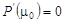, но в нашем случае имеем:

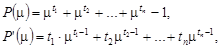
так как 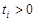, , то при 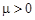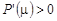, т.е. производная, если и имеет корни, то только отрицательные (из числа вещественных, конечно).

Однако, несколько сужая общность, мы можем предположить, что все значения Т – четные числа. Тогда наши рассуждения не потеряли силу и в случае отрицательных корней. Пусть 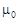– кратный корень, тогда:

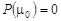и 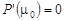. (1.14)

Покажем, что в этом случае кроме решения есть еще решение 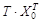. В самом деле, подставляя в (1.1) получим:

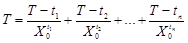. (1.15)

Отсюда

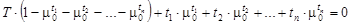
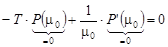– верное равенство в силу (1.14).

В силу линейности уравнения (1.1) решением являются все функции вида: .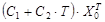

Аналогично, можно показать, что если корень имеет кратность S, то решениями соответствующими такому корню являются многочлены вида:

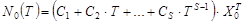Это очень похоже на аналогичную ситуацию в теории обыкновенных дифференциальных уравнений с постоянными коэффициентами.

Все наши предыдущие рассуждения остаются в силе:

;

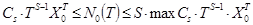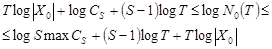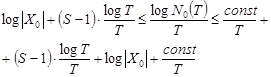При 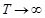имеем 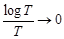и по прежнему 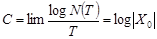, где 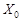– наибольший по модулю вещественный корень (возможно даже и кратный).

Наше доказательство было бы совсем полным, если бы мы показали, что задача не имеет других линейно независимых решений, кроме тех, которые мы привели. Но на самом деле ситуация намного более интересная. Наше первоначальное предположение о том, что постоянные 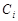являются постоянными, вообще говоря, не верно. Легко понять, что они являются произвольными (!) периодическими функциями с периодом равным 1. Так как, мы рассматриваем только целочисленные функции целочисленного аргумента, то эти периодические функции будут принимать в целых точках одно и тоже значение. Это значение мы и обозначили через 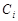. Отсюда понятно насколько велико отличие между уравнениями в конечных разностях и обыкновенными дифференциальными уравнениями. В случае обыкновенных дифференциальных уравнений произвольные постоянные действительно постоянные. Перефразируя одно удачное выражение С.Г. Крейна, здесь «незримая рука из вещественной оси» воздействует на значения в целых точках. Если понимать это более широко, то можно сказать, что это «анализ» воздействует на «теорию чисел». Смотря, конечно, чья рука… По-видимому впервые это удалось руке Эйлера. Именно Эйлер начал рассматривать конечные разности бесконечных числовых последовательностей для изучения свойств натуральных чисел. Это только название такое: дзета-функция Римана, а придумал то её Эйлер. Аналогия с обыкновенными дифференциальными уравнениями здесь обманчива. Множество решений алгебраических конечно разностных уравнений при очень широких предположениях всюду плотно во множестве решений алгебраических дифференциальных уравнений и это позволяет аппроксимировать решения последних заменяя дифференциальные уравнения уравнениями в конечных разностях. Обратное не верно. Справедлива, например, теорема Гёльдера:

Г – функция Эйлера не является решением ни одного алгебраического обыкновенного дифференциального уравнения. Хотя 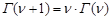, т.е. 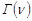– решение конечно разностного уравнения. Напомним, что Г – функция Эйлера определяется в форме интеграла, зависящего от параметра в виде:

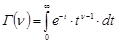Отметим теперь, что далее, если это не оговорено специально, мы рассматриваем только целочисленные решения. Более общо: мы изучаем дискретный объект с дискретной областью определения. Иными словами, отличие от систем массового обслуживания здесь имеет принципиальный характер, последние изучают дискретный объект с непрерывной областью определения.

Достаточно подробно теория конечных разностей изложена в монографии А.О. Гельфонда «Исчисление конечных разностей» часть 1, ОНТИ, 1936 г., 1963 г. – полный вариант монографии, 1-е издание 1952 год; 4-е издание 2006 г. Там же можно найти, например, доказательство теоремы Гёльдера.

Возвращаясь к примеру с телеграфом, можно получить уравнение:

приближенное значение пропускной способности 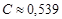. (см. К. Шеннон, Работы по теории информации и кибернетике, М. ИЛ., 1963 г., статья «Математическая теория связи»).

При блоковой передаче данных аналогичные рассуждения приводят к системе разностных уравнений. Характеристическое уравнение (1.3) принимает теперь вид:

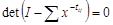. (1.16)

Аналогично предыдущему можно показать, что и в этом случае:

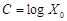где 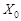– максимальный корень уравнения (1.16).

Возвращаясь к характеристическому уравнению модели работы телеграфа, найдем его приближенное решение. Для этого доставим в правую часть этого уравнения все положительные степени 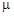, мы при этом не слишком ошибемся, т.к. искомый корень 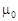меньше единицы и поэтому 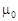в больших степенях мало:

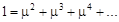
Отсюда:

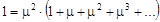Замечая, что в круглых скобках стоит сумма геометрической прогрессии со знаменателем меньшим единицы, получим:

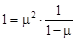Откуда:

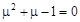И мы пришли к решению обычного квадратного уравнения. Положительный корень этого уравнения такой:

а соответствующее значение:

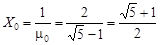Это число называется «золотым сечением» и мы еще поговорим о нем позднее в связи с числами Фибоначчи и пропускной способностью алгоритма Эвклида.

А сейчас заметим, что:

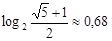Сравните это с числом, найденным К. Шенноном и, вспомните, что у него не было компьютера. И, следовательно, корень многочлена 10-й степени он вынужден был искать приближенным способом, возможно используя метод Лобачевского.

Дата добавления: 2018-09-22; просмотров: 274; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!