Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
Владимирский государственный университет
имени А. Г. и Н. Г. Столетовых
Институт машиностроения и автомобильного транспорта
Кафедра «Управление качеством и техническое регулирование»
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ:
«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ»
Обработка результатов измерений линейного размера конструкции здания
Вариант №21
Выполнили:
Студент гр. …
Проверил:
к.т.н., доцент Арефьев Е.В.
Владимир 2018
Содержание
| 1. Задание и исходные данные 2. Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений 3. Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений |
Задание и исходные данные
Используя ряд многократных измерений линейного размера ( L ) конструкции здания, приведенный в нижеприведенной таблице задания, умноженных на порядковый номер студента в журнале учебной группы, выполнить:
1) расчёт абсолютной, относительной и приведенной погрешностей результатов измерений;
2) выделение аддитивной и мультипликативной составляющих из абсолютной и относительной погрешностей результатов измерений, построить их графические зависимости
|
|
|
Таблица №1
Результаты измерений линейного размера L (в сантиметрах)
| № измерения | Li | № измерения | Li |
| 1 | 1,2 | 9 | 1,2 |
| 2 | 1,1 | 10 | 1,1 |
| 3 | 0,8 | 11 | 1,3 |
| 4 | 1,4 | 12 | 1,4 |
| 5 | 0,9 | 13 | 1,2 |
| 6 | 1,2 | 14 | 1,5 |
| 7 | 1,3 | 15 | 1,4 |
| 8 | 1,0 | 16 | 1,6 |
Все приведенные результаты измерений проводились одним и тем же средством измерений, в одних и тех же внешних условиях, одним и тем же субъектом измерения, с одинаковой тщательностью.
При проведении всех расчётов за истинное (действительное) значение линейного размера (L) принять значение равное 1.1 см, умноженному на порядковый номер студента в журнале учебной группы.
Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений
Определение «погрешность» является одним из центральных в метрологии, в котором используются понятия «погрешность результата измерения» и «погрешность средства измерения».
Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой физической величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины. Это значение находится экспериментальным путем и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него.
|
|
|
Погрешность средства измерения − разность между показаниями СИ и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых данным средством.
По способу количественного выражения погрешности измерения делятся на абсолютные, относительные и приведенные.
Абсолютной погрешностью ∆, выражаемой в единицах измеряемой величины, называется отклонение результата измерения «X» от истинного значения «Xи»:
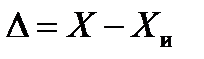 (2.1)
(2.1)
Абсолютная погрешность характеризует величину и знак полученной погрешности, но не определяет качество самого проведенного измерения.
Относительной погрешностью δ называется отношение абсолютной погрешности измерения к истинному значению измеряемой величины:
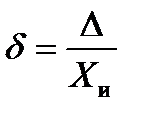 (2.2)
(2.2)
|
|
|
Погрешность δ часто выражают в процентах:
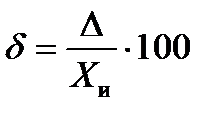 [%].
[%].
Приведенной погрешностью δпр, выражающей потенциальную точность измерений, называется отношение абсолютной погрешности ∆, к некоторому нормирующему значению XN (например, к конечному значению шкалы прибора или сумме конечных значений шкал при двухсторонней шкале):
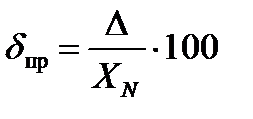 [%]. (2.3)
[%]. (2.3)
Представим результаты измерений линейного размера L (в сантиметрах) элемента конструкции (таблица №1 задания) с учетом порядкового номера «21» студента, в виде:
Таблица №2.1
Результаты измерений линейного размера L (в сантиметрах) с учётом порядкового номера студента
| № измерения | Li | № измерения | Li |
| 1 | 25,2 | 9 | 25,2 |
| 2 | 23,1 | 10 | 23,1 |
| 3 | 16,8 | 11 | 27,3 |
| 4 | 29,4 | 12 | 29,4 |
| 5 | 18,9 | 13 | 25,2 |
| 6 | 25,2 | 14 | 31,5 |
| 7 | 27,3 | 15 | 29,4 |
| 8 | 21 | 16 | 33,6 |
Истинное (действительное) значение линейного размера (L) элемента конструкции с учётом задания составит 23,1 см (Получилось следующим образом 1,1×21=23,1). Тогда, применяя выражение (2.1), рассчитаем суммарные (т.е. содержащие аддитивные и мультипликативные составляющие) абсолютные погрешности (Δсi) для каждого измерения:
|
|
|
Результаты расчётов суммарных абсолютных погрешностей приведены в таблице 2.2.
Таблица №2.2
Суммарные абсолютные погрешности
| № измерения | 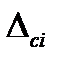 , см , см
| № измерения | 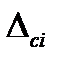 , см , см
|
| 1 | 25,2-23,1=2,1 | 9 | 2,1 |
| 2 | 23,1-23,1=0 | 10 | 0 |
| 3 | 16,8-23,1=-6,3 | 11 | 4,2 |
| 4 | 6,3 | 12 | 6,3 |
| 5 | -4,2 | 13 | 2,1 |
| 6 | 2,1 | 14 | 8,4 |
| 7 | 4,2 | 15 | 6,3 |
| 8 | -2,1 | 16 | 10,5 |
Применяя полученные значения суммарной абсолютной погрешности (Δсi), рассчитаем среднее значение абсолютной погрешности Δсрпо зависимости вида:
 (2.4)
(2.4)
Используя рассчитанные значения суммарной абсолютной погрешности (Δсi), рассчитываются суммарные относительные погрешности измерений (δсi), применяя зависимость вида (2.2):
Таблица 2.3
Суммарные относительные погрешности
| № измерения | δсi, % | № измерения | δсi, % |
| 1 | 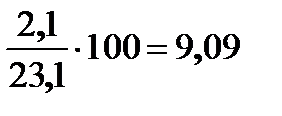
| 9 | 9,09 |
| 2 | 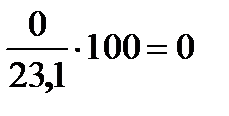
| 10 | 0,00 |
| 3 | 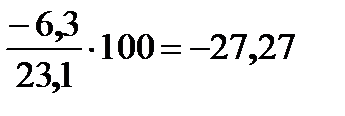
| 11 | 18,18 |
| 4 | 27,27 | 12 | 27,27 |
| 5 | -18,18 | 13 | 9,09 |
| 6 | 9,09 | 14 | 36,36 |
| 7 | 18,18 | 15 | 27,27 |
| 8 | -9,09 | 16 | 45,45 |
Применяя полученные значения суммарной относительной погрешности (δсi), рассчитаем среднее значение абсолютной погрешности (δ ср) по зависимости вида:
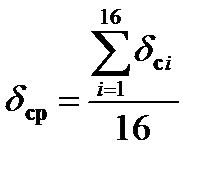 (2.5)
(2.5)
Подставив в формулу (2.5) необходимые данные из таблицы 2.3, получим 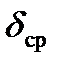
11,36%.
Для расчёта приведенной погрешности результатов измерений, в соответствии с формулой (2.3), необходимо знание нормирующего значения XN, которое, в соответствии с заданием, не определено. Поэтому, учитывая реальные линейные размеры элемента конструкции здания, допустим, что средство измерения этих размеров имеет конечное значение шкалы, например, 50 см.
Тогда средняя приведенная погрешность, с учётом выше рассчитанного значения Δср 2.625 см, составит:
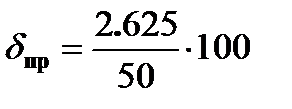 = 5,25%
= 5,25%
Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений.
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности:
● аддитивные ∆а, не зависящие от измеряемой величины;
● мультипликативные ∆м, которые прямо пропорциональны измеряемой величине;
●нелинейные ∆н, имеющие нелинейную зависимость от измеряемой величины.
Эти погрешности применяют в основном для описания метрологических характеристик СИ. Разделение погрешностей на аддитивные, мультипликативные и нелинейные весьма существенно при решении вопроса о нормировании и математическом описании погрешностей СИ.
Примеры аддитивных погрешностей − от постоянного груза на чашке весов, от неточной установки на нуль стрелки прибора перед измерением, от термо-ЭДС в цепях постоянного тока. Причинами возникновения мультипликативных погрешностей могут быть: изменение коэффициента усиления усилителя, изменение жесткости мембраны датчика манометра или пружины прибора, изменение опорного напряжения в цифровом вольтметре.
Данные разновидности погрешностей иногда называют также так:
● аддитивные---- погрешность нуля;
● мультипликативные-----погрешность крутизны характеристики;
● нелинейные--------- погрешность нелинейности.
В связи с тем, что аддитивная и мультипликативная составляющие погрешности характерны для средства измерения, причём в диапазоне измеряемых величин, то исходя из заданного истинного (действительного) значения линейного размера элемента конструкции (23,1см), допустим, что использованное средство измерений, позволяет производить измерения в диапазоне от 5 см до 50 см, причём обладает единой для всей шкалы средней относительной погрешностью 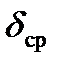 11,36%, которое рассчитано по формуле (2.5) в 2-ом разделе данной работы. Исходя из выбранного диапазона измерений средства измерений (5см – 50 см), возьмём из него, например, 10 равноудалённых фиксированных (эталонных) значений линейного размера элемента конструкции, включая заданное истинное (действительное) значение, равное 23,1 метра. В результате ряд измеряемых эталонных значений линейных размеров Lэтi, использованным средством измерения, будет иметь вид: 5; 10; 15; 20; 25; 30; 35; 40; 45; 50 (см).
11,36%, которое рассчитано по формуле (2.5) в 2-ом разделе данной работы. Исходя из выбранного диапазона измерений средства измерений (5см – 50 см), возьмём из него, например, 10 равноудалённых фиксированных (эталонных) значений линейного размера элемента конструкции, включая заданное истинное (действительное) значение, равное 23,1 метра. В результате ряд измеряемых эталонных значений линейных размеров Lэтi, использованным средством измерения, будет иметь вид: 5; 10; 15; 20; 25; 30; 35; 40; 45; 50 (см).
Используя выражение (2.5), можно определить значения суммарной абсолютной погрешности для всех членов ряда (Lэтi), а именно:
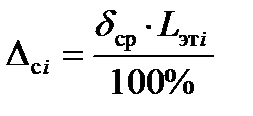 (2.5)
(2.5)
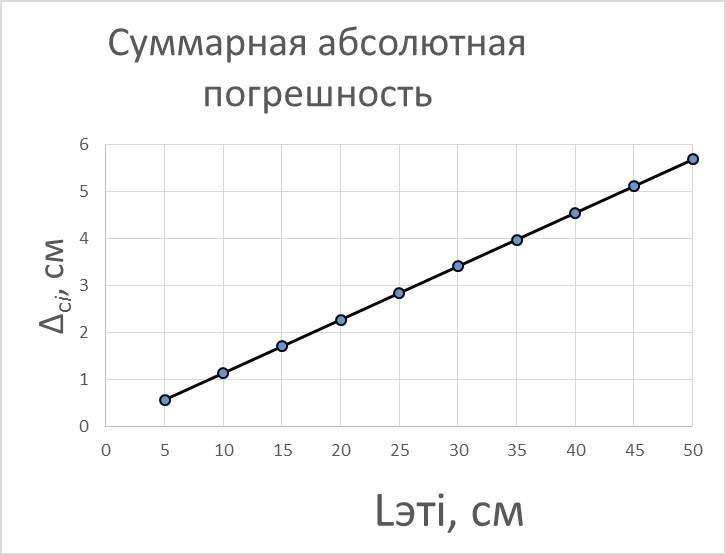
Рассчитанные значения суммарной абсолютной погрешности ∆сi для всех членов ряда, с учётом выполнения правил округления результатов измерений и погрешностей измерений (приведены в Приложении 1), представлены в таблице 3.1.
Таблица 3.1
Результаты расчетов суммарной, аддитивной и мультипликативной
абсолютных погрешностей
| № члена ряда | Lэтi ,м | 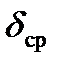 , % , %
| ∆сi, см | Δа, см | Δм, см |
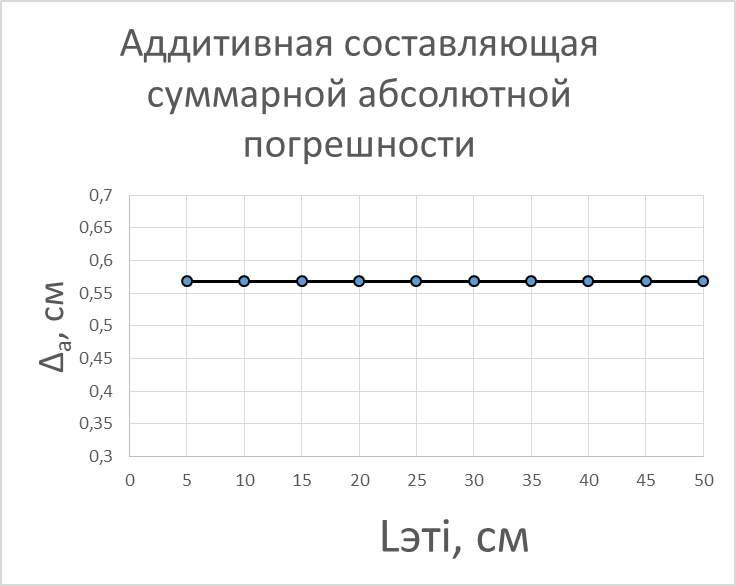
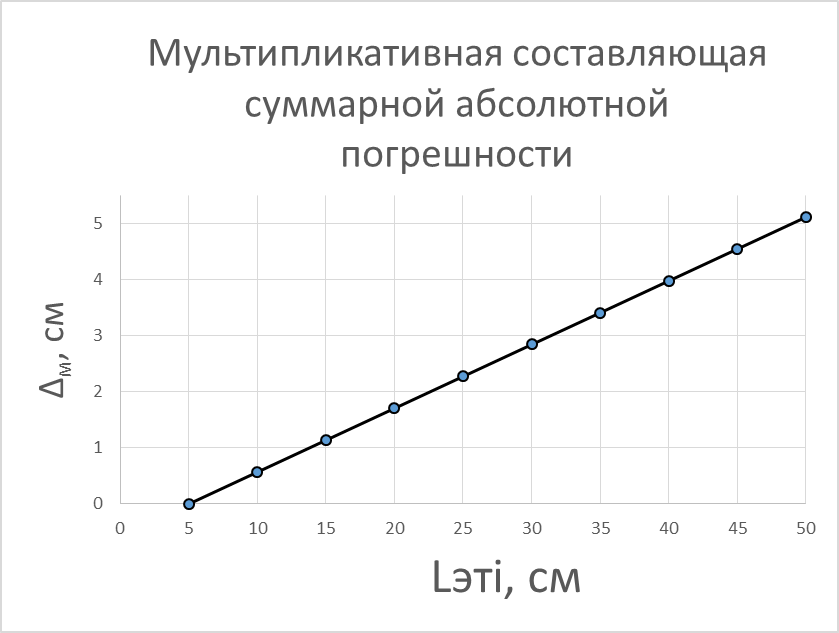
| 1 | 5 | 11,36 | 0,568 | 0,568 | 0 |
| 2 | 10 | 11,36 | 1,136 | 0,568 | 0,568 |
| 3 | 15 | 11,36 | 1,704 | 0,568 | 1,136 |
| 4 | 20 | 11,36 | 2,272 | 0,568 | 1,704 |
| 5 | 25 | 11,36 | 2,84 | 0,568 | 2,272 |
| 6 | 30 | 11,36 | 3,408 | 0,568 | 2,84 |
| 7 | 35 | 11,36 | 3,976 | 0,568 | 3,408 |
| 8 | 40 | 11,36 | 4,544 | 0,568 | 3,976 |
| 9 | 45 | 11,36 | 5,112 | 0,568 | 4,544 |
| 10 | 50 | 11,36 | 5,68 | 0,568 | 5,112 |
Результаты расчётов относительных составляющих погрешностей измерений
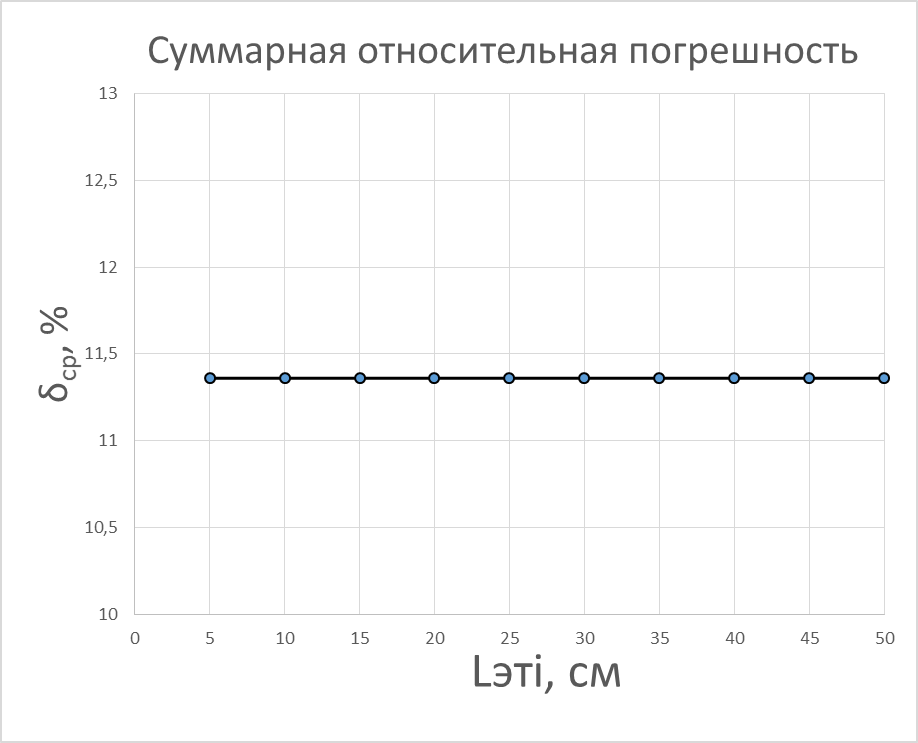
| № члена ряда | Lэтi ,см | δср, % | δаi , % | δмi , % |
| 1 | 5 | 11,36 | 11,360 | 0,000 |
| 2 | 10 | 11,36 | 5,680 | 5,680 |
| 3 | 15 | 11,36 | 3,787 | 7,573 |
| 4 | 20 | 11,36 | 2,840 | 8,520 |
| 5 | 25 | 11,36 | 2,272 | 9,088 |
| 6 | 30 | 11,36 | 1,893 | 9,467 |
| 7 | 35 | 11,36 | 1,623 | 9,737 |
| 8 | 40 | 11,36 | 1,420 | 9,940 |
| 9 | 45 | 11,36 | 1,262 | 10,098 |
| 10 | 50 | 11,36 | 1,136 | 10,224 |
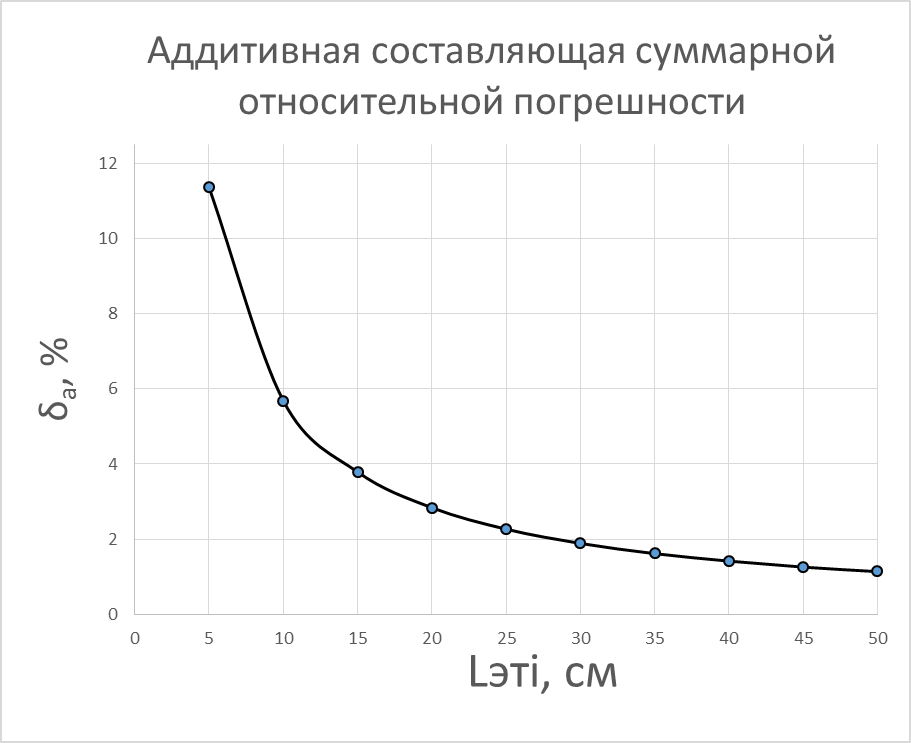
Аддитивная составляющая относительной погрешности:
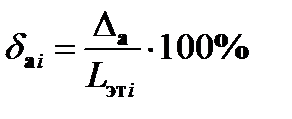
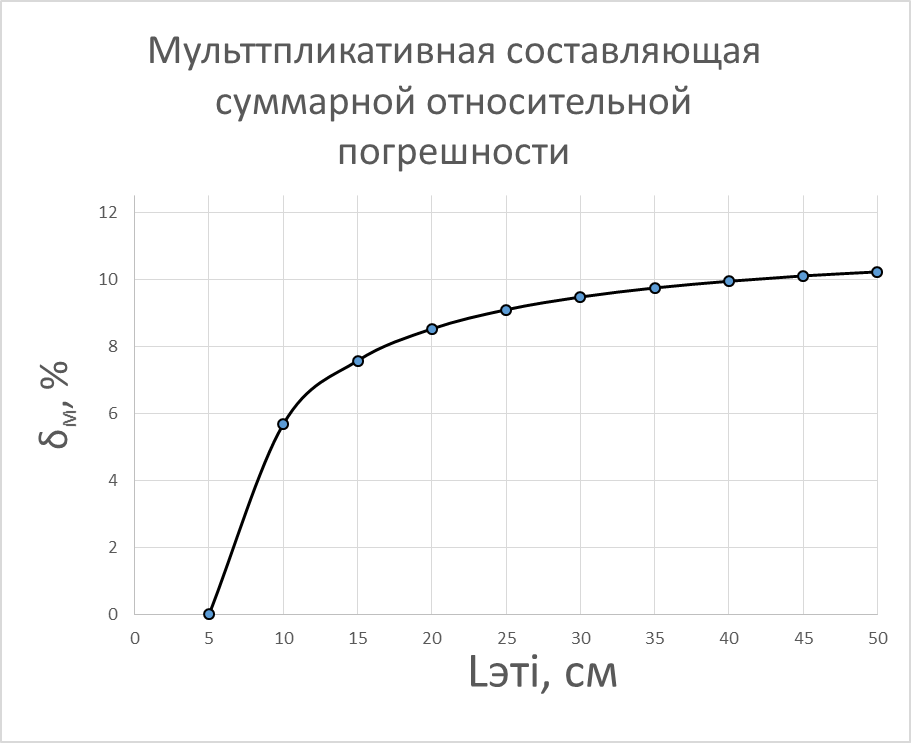
Мультипликативная составляющая относительной погрешности:
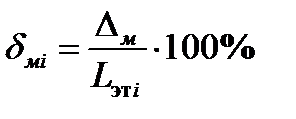
Выводы
Таким образом, выполнен расчёт абсолютной, относительной и приведенной погрешностей результатов измерений. Выделены аддитивная и мультипликативная составляющие из абсолютной и относительной погрешностей результатов измерений, построены их графические зависимости.
Список использованной литературы
1) Сергеев А.Г., Крохин В.В. Метрология: Учеб.пособие для вузов.М.: Логос,2000.-408с.
2) Метрология и электрорадиоизмеренияв телекоммуникационных системах:учебник для вузов-В.И.Нефедов, В.И.Хахин, Е.В.Федорова и др,;Под ред. В.И.Нефедова.-М.:Высш.шк.,2001-381 с.
3) Алиев Т.М.,Тер-Хачатуров А.А. Измерительная техника:Учеб. пособие для техн. вузов.-М.:Высш.шк.,1991.-384с.
4) Методические указания к практическим занятиям по курсу «Теоретическая метрология» / Под ред. А.Г.Сергеева. Сост.: А.Г.Сергеев и др.,Владим. гос. ун-т ; Владимир, 1997, 64 с.
5) Куприянов В.Е. Общая теория измерений: в 2 ч. Ч.2.Методы измерений. Математические модели. Погрешности и обработка результатов измерений: учеб.пособие/В.Е.Куприянов, Э.Ф.Касаткина; Владим.гос.ун-т – Владимир: ВлГУ,2005. -148 с.
Дата добавления: 2018-09-20; просмотров: 4270; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
