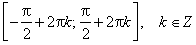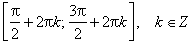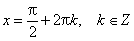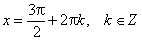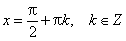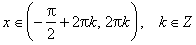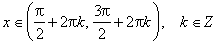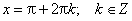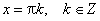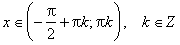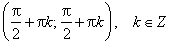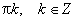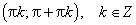Обратные тригонометрические функции
105.1)
Заметим, что для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

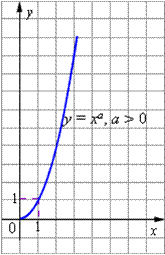
К основным свойствам степенной функции y = x a при a > 0 относятся:
- Область определения функции - промежуток (0; +
 ).
). - Область значений функции - промежуток (0; +
 ).
). - Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно возрастает в области определения функции, то есть, если x1 < x2 то ar1 < ar2 .
- График степенной функции при a > 0 изображен на рисунке.
| 
|
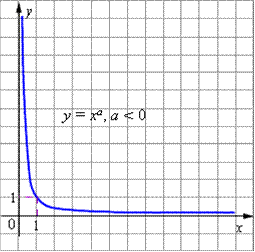
К основным свойствам степенной функции y = x a при a < 0 относятся:
- Область определения функции - промежуток (0; +
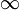 ).
). - Область значений функции - промежуток (0; +
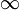 ).
). - Для любых a график функции проходит через точку (1; 1).
- Функция строго монотонно возрастает в области определения функции, то есть, если x1 < x2 то ar1 > ar2 .
- График степенной функции при a < 0 изображен на рисунке.
105.2)мы определили значение выражения ax для всех a > 0 и всех x. Если a = 1, то ax = 1 при всех x. Следовательно, при a > 0, a ≠ 1, определена функция y = ax, отличная от постоянной. Эта функция называется показательной функцией с основанием a. К основным свойствам показательной функции y = ax при a > 1 относятся:
- Область определения функции − вся числовая прямая.
- Область значений функции − промежуток

- Функция строго монотонно возрастает на всей числовой прямой, то есть, если
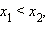 то
то 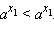
- График показательной функции с основанием a > 1 изображён на рисунке.
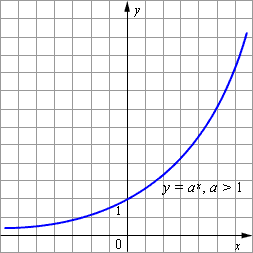
|
| Рисунок 2.2.5.1. Функция y = ax при a > 1 |
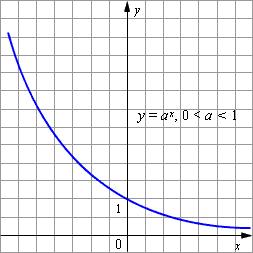
|
| Рисунок 2.2.5.2. Функция y = ax при 0 < a < 1 |
К основным свойствам показательной функции y = ax при 0 < a < 1 относятся:
|
|
|
- Область определения функции − вся числовая прямая.
- Область значений функции − промежуток

- Функция строго монотонно убывает на всей числовой прямой, то есть, если
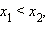 то
то 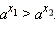
- График показательной функции с основанием 0 < a < 1 изображён на рисунке.
105.3)
Функция вида y = loga х(где а > 0, а ≠ 1) называется логарифмической.
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0.
2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа b есть такое положительное число x, что logax = b, т.е. уравнение logax = b имеет корень. Такой корень существует и равен x = ab, так как logaab = b.
3) Логарифмическая функция y = logax является возрастающей на промежутке x > 0, если a > 0, и убывающей, если 0 < a < 1.
|
|
|
4) Если a > 0, то функция y = logax принимает положительные значения при x > 1,отрицательные — при 0 < x < 1. Если 0 < a < 1, то функция y = logax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1.
Это следует из того, что функция y = logax принимает значение , равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если a > 1, и убывающей, если 0 > a > 1.
Ниже представлены графики логарифмических функций при a > 0 (1); 0 > a >1 (2).
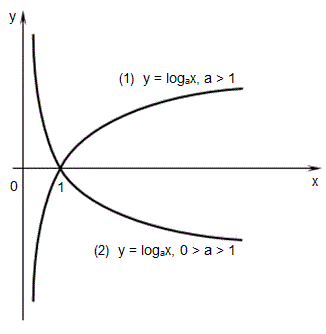
Стоит отметить, что график любой логарифмической функции y = logax проходит через точку (1 ; 0)
106.1)
Функция синус
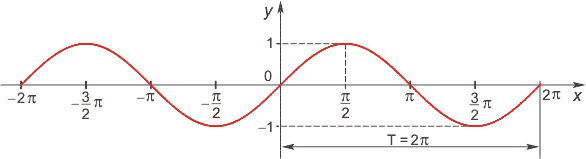
| ||||||||
Область определения функции— множество Rвсех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R.
sin x = 0 при x = π·k, k ∈ Z.
sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z.
sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
|
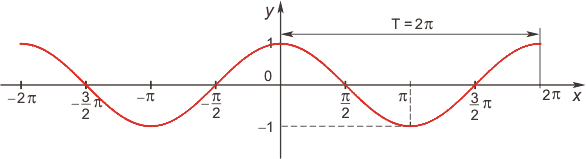
Функция косинус
|
|
|
| ||||||||||||||
Область определения функции— множество Rвсех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R.
|
Функция тангенс
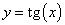
| ||||||||||||
Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения.
Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения.
|
Функция котангенс
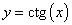
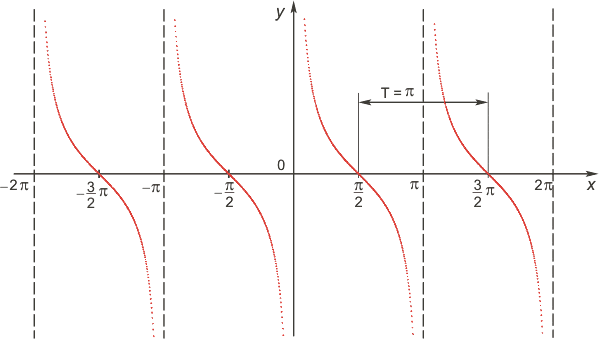
| ||||||||||
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная. Функция нечетная: ctg(−x)=−ctg x для всех х из области определения. Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π·k)=ctg x, k ∈ Z для всех х из области определения.
|
106.2)
Обратные тригонометрические функции
| |
| График 2.3.4.1. График функции y = arcsin x. |
| |
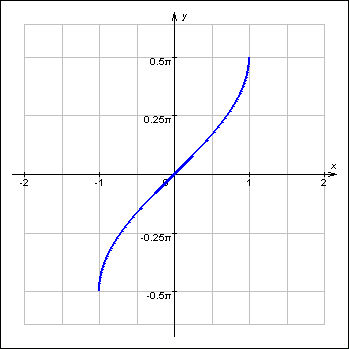
| График 2.3.4.2. График функции y = arccos x. |
Арксинусом x называют такое число  , что sin t = x. Из определения следует, что
, что sin t = x. Из определения следует, что

|
При помощи арксинуса решение уравнения sin x = t записывается следующим образом:
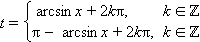 или t = (–1)n arcsin x + πn, или t = (–1)n arcsin x + πn, 
|
Функция y = arcsin x определена и непрерывна на отрезке [–1; 1]. Ее областью значений является отрезок 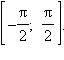 Она обратна функции y = sin x, рассматриваемой на отрезке
Она обратна функции y = sin x, рассматриваемой на отрезке 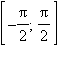 и поэтому монотонно возрастает. Функция y = arcsin x является нечетной.
и поэтому монотонно возрастает. Функция y = arcsin x является нечетной.
Арккосинусом x называют такое число 0 ≤ t ≤ π, что cos t = x. Из определения следует, что
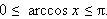
|
При помощи арккосинуса решение уравнения cos x = t записывается следующим образом:
t = ±arccos x + 2πn, 
|
Функция y = arccos x определена и непрерывна на отрезке [–1; 1]. Ее областью значений является отрезок [0; π]. Она обратна функции y = cos x, рассматриваемой на отрезке [0; π], и поэтому монотонно убывает на области определения. Функция y = arccos x не является ни четной, ни нечетной.
Арктангенсом x называют такое число  , что tg t = x. При помощи арктангенса решение уравнения tg x = t записывается следующим образом:
, что tg t = x. При помощи арктангенса решение уравнения tg x = t записывается следующим образом:
t = arctg x + πn, 
|
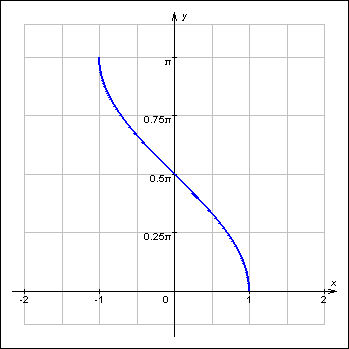
Функция y = arctg x является нечетной.
| |
| График 2.3.4.3. График функции y = arctg x. |
| |
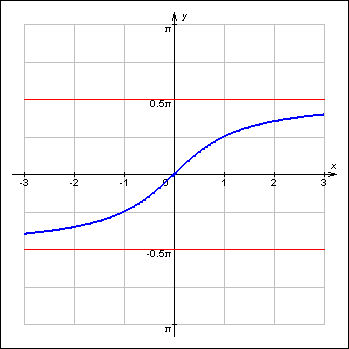
| График 2.3.4.4. График функции y = arcctg x. |
Арккотангенсом x называют такое число 0 ≤ t ≤ π, что ctg t = x. При помощи арккотангенса решение уравнения ctg x = t записывается следующим образом:
t = arcctg x + πn, 
|
Функция y = arcctg x не является ни четной, ни нечетной.
Функции y = arctg x и y = arcctg x определены и непрерывны на всей числовой оси. Их областями значений являются, соответственно, интервалы  и (0; π). Арктангенс монотонно возрастает, а арккотангенс монотонно убывает на всей области определения. Функциями, обратными к данным, являются соответственно tg x на
и (0; π). Арктангенс монотонно возрастает, а арккотангенс монотонно убывает на всей области определения. Функциями, обратными к данным, являются соответственно tg x на 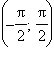 и ctg x на(0;
и ctg x на(0;
Дата добавления: 2018-08-06; просмотров: 301; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!