Точки экстремума функции двух переменных. Необходимый признак экстремума (доказательство), формулировка достаточного признака экстремума функции двух переменных.
1
Определение функции двух переменных
Предел функции z=f(x,y) вточке (x0,y0)
Функцией двух переменных называется закон, по которому каждой паре значений независимых переменных 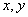 (аргументов) из области определения соответствует значение зависимой переменной
(аргументов) из области определения соответствует значение зависимой переменной  (функции).
(функции).
Данную функцию обозначают следующим образом:
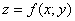 либо
либо 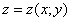 , или же другой стандартной буквой:
, или же другой стандартной буквой: 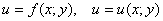

2
Частные приращения функции двух переменных, их геом смысл

Частные производные
Каждая частная производная (по x и по y) функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении другой переменной:

(где y = const),
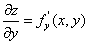
(где x = const).
Поэтому частные производные вычисляют по формулам и правилам вычисления производных функций одной переменной, считая при этом другую переменную постоянной (константой).

3
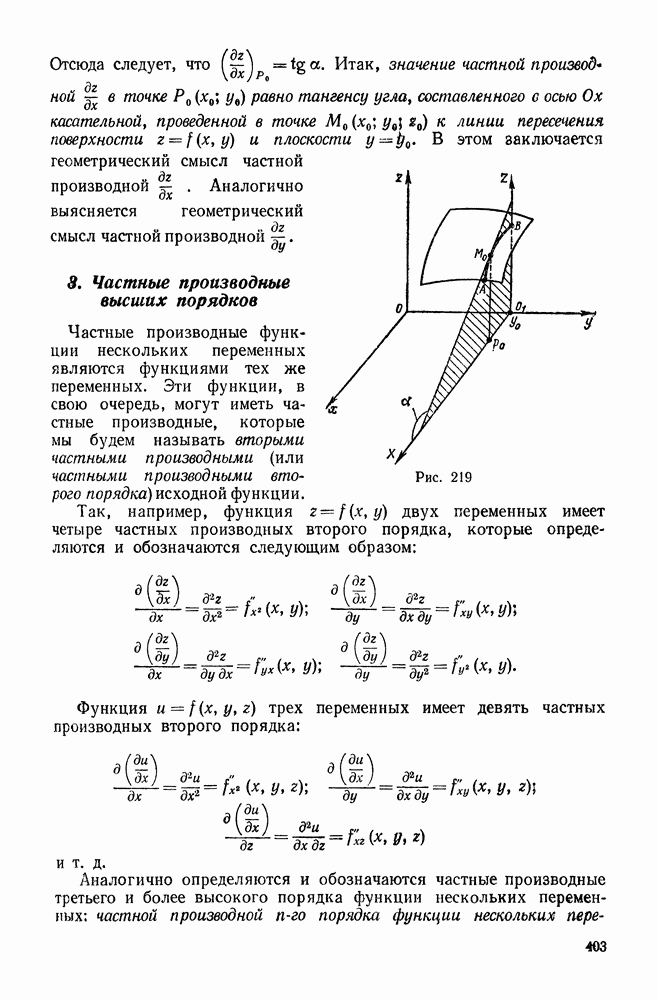
Полное приращение функции двух переменных
Непрерывность функции двух переменных в точке (опр)
Непрерывность функции двух переменных в ограниченной замкнутой области
Свойства функции непрерывных в ограниченной замкнутой области

| Непрерывность функции двух переменных | |
|

|
|
|
4
Определение дифференцируемой функции двух переменных
Определение полного дифференциала функции двух переменных
Необходимые условия дифференцируемости (с выводом)
Формулировка достаточного условия дифференцируемости
§ 4. Дифференцируемость функции
нескольких переменных
Дифференцируемые функции нескольких переменных.
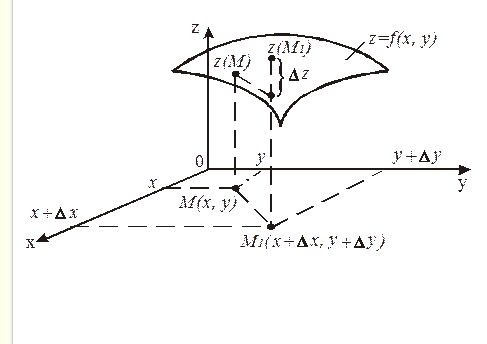
Пусть функция двух переменных 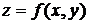 определена в некоторой открытой области
определена в некоторой открытой области 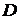 плоскости
плоскости 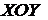 ,
, 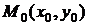 – точка области
– точка области 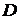 . Придавая переменным приращения
. Придавая переменным приращения  и
и 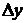 , перейдем из точки
, перейдем из точки  в какую-нибудь точку
в какую-нибудь точку 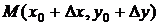 той же области. При этом функция
той же области. При этом функция 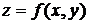 получит приращение
получит приращение
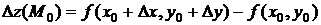 .
.
В отличие от частных приращений 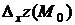 и
и  это приращение называется полным приращениемфункции
это приращение называется полным приращениемфункции 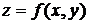 в точке
в точке  , соответствующим приращениям
, соответствующим приращениям  и
и 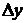 независимых переменных.
независимых переменных.
ОПРЕДЕЛЕНИЕ. Функция 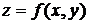 называется дифференцируемойв точке
называется дифференцируемойв точке 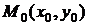 если ее полное приращение в этой точке может быть записано в виде
если ее полное приращение в этой точке может быть записано в виде
|
|
|
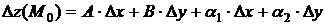 , (4.1)
, (4.1)
где 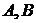 – некоторые числа,
– некоторые числа, 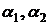 – бесконечно малые при
– бесконечно малые при 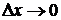 ,
, 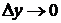 (или, короче при
(или, короче при 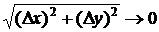 ).
).
Замечание. Функции  и
и  зависят от
зависят от 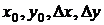 .
.
Функция , дифференцируемая в каждой точке некоторой области, называется дифференцируемой в этойобласти.
Соотношение (4.1) можно записать и в более сжатой форме:
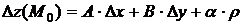 (4.2)
(4.2)
где 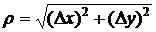 ,
, 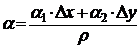 – бесконечно малая при
– бесконечно малая при 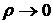 .
.
Слагаемое 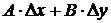 , линейное относительно
, линейное относительно  и
и 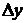 , является главной частью приращения, так как оставшееся слагаемое
, является главной частью приращения, так как оставшееся слагаемое 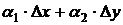 (или
(или  , если используется формула (4.2)) есть бесконечно малая более высокого порядка чем
, если используется формула (4.2)) есть бесконечно малая более высокого порядка чем  и
и 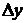 .
.
Дифференцируемость функции нескольких переменных
Теорема 1 (связь дифференцируемости и непрерывности). Если функция  дифференцируема в точке
дифференцируема в точке  , то она и непрерывна в этой точке.
, то она и непрерывна в этой точке.
►Действительно, поопределениюфункции, дифференцируемойвточке  , ее приращение представимо в виде
, ее приращение представимо в виде
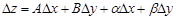 ,
,
где 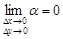 ;
; 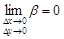 ;
; 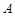 ,
,  – некоторые числа, не зависящие от
– некоторые числа, не зависящие от 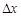 и
и 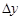 . Следовательно,
. Следовательно,
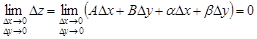 ,
,
а это означает, что функция 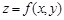 непрерывна в точке
непрерывна в точке  . ◄
. ◄
Теорема 2 (необходимое условие дифференцируемостифункции нескольких переменных). Если функция  дифференцируема в точке
дифференцируема в точке  , то она имеет в этой точке частные производные
, то она имеет в этой точке частные производные 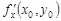 и
и  , причем
, причем 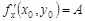 ,
,  .
.
|
|
|
►Пустьфункция 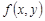 дифференцируема в точке
дифференцируема в точке  , тогда ее приращение представимо в виде (1). Положив в формуле (1)
, тогда ее приращение представимо в виде (1). Положив в формуле (1) 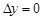 , имеем
, имеем 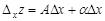 . Разделив это равенство на
. Разделив это равенство на 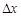 и перейдя к пределу при
и перейдя к пределу при 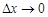 , получим
, получим
 .
.
Следовательно, в точке  существует частная производная
существует частная производная 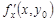 .
.
Аналогично доказывается существование частной производной  в точке
в точке  . ◄
. ◄
Замечание. Утверждения, обратные утверждениям теорем 1 и 2 неверны, т.е. из непрерывности функции, а также существования ее частных производных, еще не следует дифференцируемость функции.
Теорема 3 (достаточное условие дифференцируемости функции нескольких переменных). Если функция  имеет частные производные в некоторой окрестности точки
имеет частные производные в некоторой окрестности точки  , непрерывные в самой этой точке, то она дифференцируема в точке
, непрерывные в самой этой точке, то она дифференцируема в точке  .
.
5
сложная функция двух переменных
Пусть 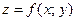 – функция двух переменных
– функция двух переменных 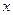 и
и 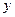 , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной 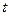 :
:  . В этом случае функция
. В этом случае функция 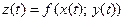 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной 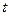 ; переменные
; переменные 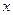 и
и 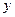 – промежуточные переменные.
– промежуточные переменные.
Теорема. Если 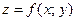 – дифференцируемая в точке
– дифференцируемая в точке  функция и
функция и  – дифференцируемые функции независимой переменной
– дифференцируемые функции независимой переменной 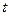 , то производная сложной функции
, то производная сложной функции 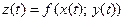 вычисляется по формуле
вычисляется по формуле
|
|
|
 . (1)
. (1)
Частный случай: 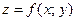 , где
, где 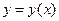 , т.е.
, т.е.  – сложная функция одной независимой переменной
– сложная функция одной независимой переменной 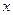 . Этот случай сводится к предыдущему, причем роль переменной
. Этот случай сводится к предыдущему, причем роль переменной 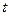 играет
играет 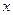 . Согласно формуле (1) имеем:
. Согласно формуле (1) имеем:
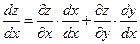
или
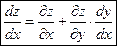 . (2)
. (2)
Формула (2) носит название формулы полной производной.
Общий случай: 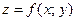 , где
, где  ,
, 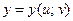 . Тогда
. Тогда 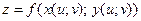 – сложная функция независимых переменных
– сложная функция независимых переменных 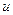 и
и 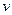 . Ее частные производные
. Ее частные производные 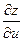 и
и 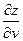 можно найти, используя формулу (1) следующим образом. Зафиксировав
можно найти, используя формулу (1) следующим образом. Зафиксировав 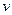 , заменяем в ней
, заменяем в ней  соответствующими частными производными
соответствующими частными производными 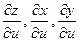 :
:
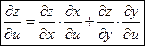 (3)
(3)
Аналогично получаем:
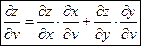 .
.
Таким образом, производная сложной функции ( 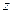 ) по каждой независимой переменной (
) по каждой независимой переменной ( 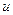 и
и 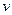 ) равна сумме произведений частных производных этой функции (
) равна сумме произведений частных производных этой функции ( 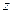 ) по ее промежуточным переменным (
) по ее промежуточным переменным ( 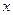 и
и 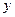 ) на их производные по соответствующей независимой переменной (
) на их производные по соответствующей независимой переменной ( 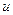 и
и 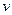 ).
).
6
неявная функция двух переменных
вывод правила дифференцирования неявной функции
Функция 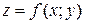 называется неявной, если она задается уравнением
называется неявной, если она задается уравнением
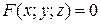 , (11)
, (11)
неразрешенным относительно z. Найдем частные производные 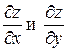 неявной функции z, заданной уравнением (11). Для этого, подставив в уравнением вместо z функцию
неявной функции z, заданной уравнением (11). Для этого, подставив в уравнением вместо z функцию 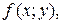 получим тождество
получим тождество 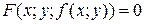 . Частные производные по х и по уфункции, тождественно равной нулю, также равны нулю:
. Частные производные по х и по уфункции, тождественно равной нулю, также равны нулю:


откуда

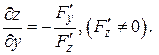 (12)
(12)
Замечания.
а) Уравнение вида (11) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение 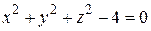 определяет функции
определяет функции 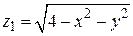 и
и  , определенные в круге
, определенные в круге 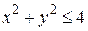 , и
, и 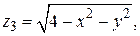 определенную в полукруге
определенную в полукруге 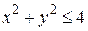 при
при  и т. д., а уравнение
и т. д., а уравнение  не определяет никакой функции.
не определяет никакой функции.
Имеет место теорема существования неявной функции двух переменных:
если функция 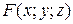 и её производные
и её производные 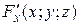 и
и  ,
,  определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 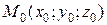 , причем
, причем 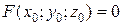 , а
, а  , то существует окрестность точки М0, в которой уравнение (11) определяет единственную функцию
, то существует окрестность точки М0, в которой уравнение (11) определяет единственную функцию 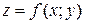 , непрерывную и дифференцируемую в окрестности точки
, непрерывную и дифференцируемую в окрестности точки 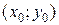 и такую, что
и такую, что  .
.
б) Неявная функция 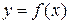 одной переменной задается уравнением
одной переменной задается уравнением  . Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
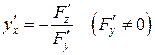 .
.


7
Частные производные высших порядков
Теорема о смешанных производных


8
Определения касательной плоскости и нормали к поверхности
Теорема о существовании касательной плоскости (с доказательством)



9
Уравнение касательной плоскости и нормали к поверхности
Геометрический смысл полного дифференциала функции двух переменных 



10
Точки экстремума функции двух переменных. Необходимый признак экстремума (доказательство), формулировка достаточного признака экстремума функции двух переменных.
Пусть функция z=f(x,y) определена и непрерывна в некоторой области G и точкаP0(x0,y0) принадлежит G.
Функция z=f(x,y) имеет в точке максимум (минимум), если существует такая окрестность этой точки, что для всех точек P(x,y) этой окрестности, отличных от P0, выполняется неравенство f(P0)›f(P) (f(P0)‹f(P)).
Максимум и минимум функции называются экстремумами функции.


Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).
Пусть в некоторой области, содержащей точку P0(x0,y0) , функция z=f(x,y) имеет непрерывные частные производные до 3–го порядка включительно и  =0 . Обозначим: ∆(P0) =
=0 . Обозначим: ∆(P0) = 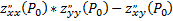 . Тогда
. Тогда
1)если ∆(P0)>0, то функция имеет экстремум в точке P0, причем это максимум, если 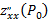 <0 и минимум, если
<0 и минимум, если 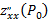 >0;
>0;
2)если ∆(P0)<0, то экстремума в точке P0 нет;
3)если ∆(P0)=0, требуется дополнительное исследование (экстремум в точке может быть или не быть).
11
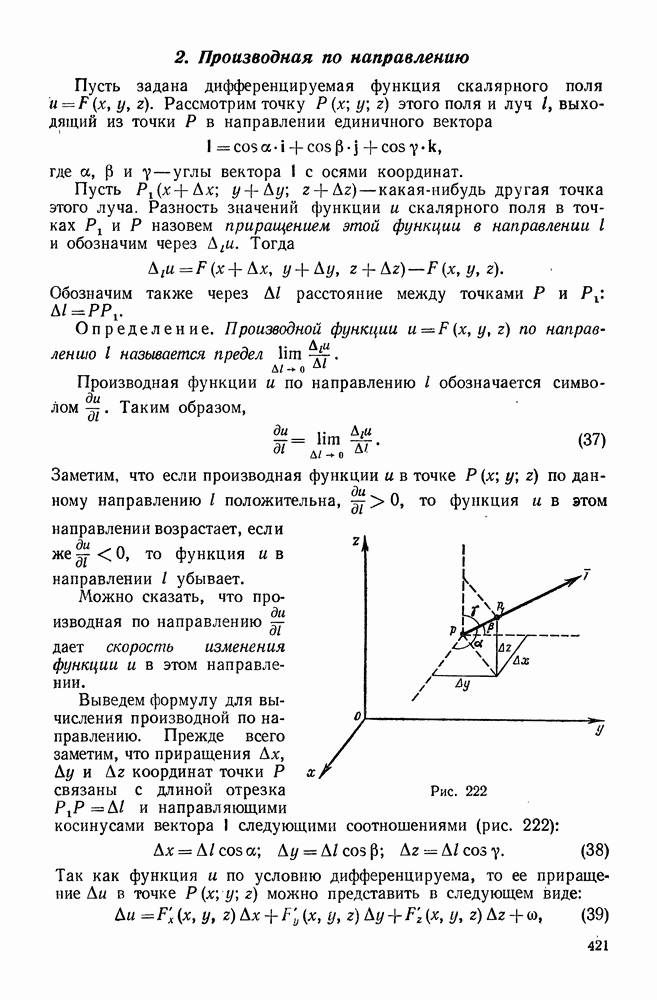
Производная по направлению, вывод правила вычисления производной по направлению. Градиент и его свойство.



12
Поверхности второго порядка.
Поверхностью второго порядка называется множество всех точек пространства,
координаты которых удовлетворяют алгебраическому уравнению второй степени
a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2a10x + 2a20y + 2a30z + a00 = 0, где
коэффициенты a11, a22, a33, a12, a13, a23, a10, a20, a30, a00 − действительныечисла, причем a11,
a22, a33, a12, a13, a23 не равны нулю одновременно.
1.Эллипсоидом называется поверхность второго порядка, которая в канонической
системе координат определяется уравнением
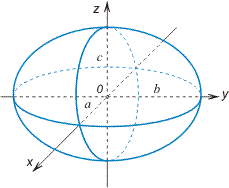
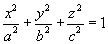
a, b, c — полуоси

2.Сфера
x2+y2+z2=R2
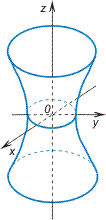
3.Однополостный гиперболоид
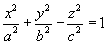
c — действительная полуось,
a и b — мнимые полуоси
 4. Двуполостный гиперболоид
4. Двуполостный гиперболоид
 c — действительная полуось,
c — действительная полуось,
a и b — мнимые полуоси

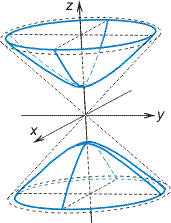
5. Конус

Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат.
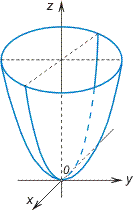
6.Эллиптический параболоид
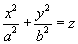
 7.Гиперболический параболоид
7.Гиперболический параболоид
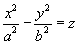
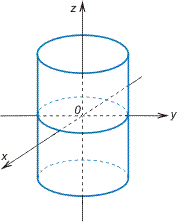
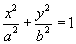 8. Эллиптический цилиндр
8. Эллиптический цилиндр
a и b — полуоси
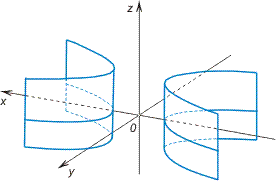 9.Гиперболический цилиндр
9.Гиперболический цилиндр
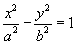
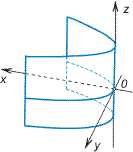 10.Параболический цилиндр
10.Параболический цилиндр

p — фокальный параметр
Дата добавления: 2018-08-06; просмотров: 1120; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 Если функция f ( x ,y ) непрерывна в точке M0(x0y0), то
Если функция f ( x ,y ) непрерывна в точке M0(x0y0), то
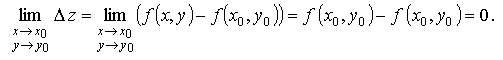 Поскольку
Поскольку
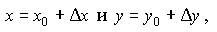
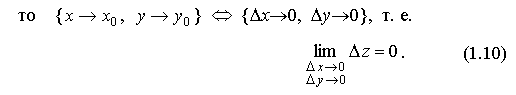 То есть, если функция f ( x ,y ) непрерывна в точке M0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращениеΔzфункции z.
То есть, если функция f ( x ,y ) непрерывна в точке M0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращениеΔzфункции z.