Различные виды уравнения прямой.

⇐ ПредыдущаяСтр 2 из 2

Рассмотрим прямую проходящую через точки М1М2, пусть М произвольная точка лежащая на этой прямой тогда векторы ММ2 и М1М являются коллинеарными. Вектор ММ2 = (X2 – X; Y2 – Y), M1M = (X - X1; Y – Y1). Из условия коллинеарности векторов, следует, что 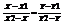1). 1) -уравнение прямой, проходящей через две заданные точки пусть X2 – X1 = K, Y2 – Y1 = L, тогда вектор a = (K; L) параллельна данной прямой направляющий вектор 1)может быть записано в виде: 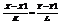2). 2) -уравнением прямой проходящей через данную точку М1 в заданном направлении 2)каноническим уравнением прямой. Если три точки М1, М2 и М лежат на одной прямой, то площадь треугольника равна нулю. 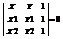3). 3)– уравнение прямой в виде определителя приравняем отношение равенства 1)к некоторому числу T. X - X1 = (X2 – X) T, X –X1 = KT; Y – Y1 = (Y2 –Y1) T, Y – Y1 = LT. (X = X1 + KT , Y = Y1 + LT 4)). 4) –называется параметрическим уравнением. Пусть на плоскости заданы две точки A и B, лежащие на координатных осях A(a; 0), B(b; 0). Найдем уравнение прямой проходящей через точки A и B. ; ; 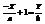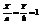- 5) . 5) –называется уравнением прямой на отрезке.

Нормальное уравнение прямой.Пусть прямаяпроходит через точку М(X; Y) перпендикулярно отрезку OP. Длина отрезка , , 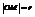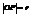cos 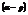, p = r(cosacos + sinasinb), p = (r cosb)cosa + (r sinb)sina. X cosa + Y sinb = p – нормальное уравнение прямой.

Расстояние от точки до прямой.

Пусть дана какая – нибудь прямая и произвольная точка М*; обозначим через d расстояние точки М* от данной прямой. Отклонением d точки М* от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и –d, если данная точка и начало координат расположены по одну сторону от данной прямой. Если даны координаты X*, Y* точки М* и нормальное уравнение прямой X cosa + Y sina - p = 0, то отклонение d точки М* от этой прямой может быть вычислено по формуле d = X* cosa + Y* sina - p. Таким образом, чтобы найти отклонение какой – нибудь точки М* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки М*. Полученное число будет равно искомому отклонению. Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: d = 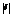. Если дано общее уравнение прямой Ax + By + C = 0, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель m, определяемый формулой . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

Взаимное расположение прямых на плоскости.

Пусть на плоскости заданы две прямые:A1x + B1y +C1 = 0 A2x + B2y + C2 = 0 – 1). Возможны следующие случаи взаимного расположения этих прямых: 1) Прямые пересекаются в одной единственной точке, это означает, что система 1) имеет единственное решение. 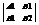¹ 0. 2) Прямые параллельны и не совпадают, это означает, что система 1)не имеет решений. В соответствии с теоремой Капели – это возможно тогда и только тогда, когда rang 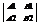не совпадает с rang 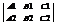. 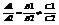3) прямые совпадают, это означает, что система 1)имеет множество решений. Это возможно тогда, когда rang 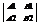совпадает с rang 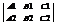. Это возможно в том случае, когда коэффициенты пропорциональны: .

Плоскость в пространстве.

В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость. Всякий вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение A(X – Xo) + B(Y – Yo) + C(Z – Zo) = 0 – 1)определяет плоскость, проходящую через точку Мо (Xo; Yo; Zo) и имеющую нормальный вектор n = {A; B; C}. Раскрывая в уравнении 1)скобки и обозначая число – AXo – BYo – CZo буквой D, представим его в виде: AX + BY + CZ + D = 0. Это уравнение называется общим уравнением плоскости. Различные виды уравнения плоскости.Пусть в пространстве заданы три различные точки М1(X1; Y1; Z1) M2(X2; Y2; Z2) M3(X3; Y3; Z3). Через эти три точки можно провести плоскость единственным образом. Рассмотрим точку M(X; Y; Z) лежащую в этой плоскости, тогда выполняется условие 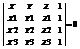- 1).Если условие 1)не выполняется, то точка М не лежит в этой плоскости, поэтому 1)называется уравнением плоскости проходящей через три заданные точки записанная в форме определителя. Раскроем определитель по элементам первой строки и обозначим коэффициенты, стоящие перед X,A; перед Y, B; перед Z, C, то тогда получим уравнение плоскости в виде AX + BY + CZ + D =0 – 2) – общее уравнение плоскости.Предположим, что 2) D ¹ 0 и рассмотрим плоскость, заданную уравнением AX + BY + CZ = 0 – 3).Очевидно, что система линейных уравнений, состоящая из равенств 2) и 3) не имеет решений. Это означает, что плоскости 2) и 3)не пересекаются. Следовательно, плоскость 3) êê2).Рассмотрим производную точку М лежащую в плоскости 3),когда вектор ОМ целиком лежит в этой плоскости вектор ОМ (X; Y: Z), поэтому 3) можно рассматривать как равное нулю, скалярного произведения векторов ОМ и N (A; B; C).Тогда из 3)следует, что вектор N перпендикулярный плоскости 3). Поэтому вектор М называется нормальным вектором плоскости, т. к. 2) êê3), то N ^ к этой плоскости, поэтому N называется нормальным вектором и для плоскости 2). - Уравнение плоскости отрезка.

Взаимное расположение плоскостей. 1) A1X + B1Y + C1Z + D1 = 0 2) A2X + B2Y + C2Z + D2 = 0. 1.Пусть плоскости 1 и 2 пересекаются. В этом случае имеются точки, принадлежащие одновременно плоскостям 1и 2. Поэтому система линейных уравнений, составленная из 1и 2 имеет по крайней мере, одно решение. Для этого необходимо и достаточно выполнения условия:

2. Если плоскость 1 параллельна 2, то это означает, что с.л.у. составленная из 1и2 не имеет решений. Для этого необходимо и достаточно выполнения условия: 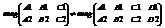3.Пусть плоскость 1и2 совпадают. .

Расстояние от точки до плоскости.Пусть точка М* - какая угодно точка пространства, d – расстояние от нее до данной плоскости. Отклонением d точки М* от данной плоскости называется число +d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число –d, если они расположены по одну сторону от данной плоскости. Если даны координаты X*, Y*,Z* точки М* и нормальное уравнение плоскости X cosa + Y cosb + Z cosg - p = 0, то отклонение d точки М* от этой плоскости может быть вычислено по формуле d = X* cosa + Y* cosb + Z* cosg - p. Очевидно d = 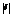. Общее уравнение плоскости Ax + By + Cz + D = 0, приводится к нормальному виду умножением на нормирующий множитель, определяемый . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

Прямая в пространстве.

Рассмотрим в пространстве две точки М1(X1; Y1; Z1) и M2(X2; Y2; Z2) можно провести единственную прямую. Пусть М(X; Y; Z) лежит на этой прямой, тогда векторы М1М2 и М1М каллинеарны М1М2(X2 – X1; Y2 –Y1; Z2 –Z1); M1M(X –X1; Y –Y1; Z – Z1). Из условия координат следует - 1). 1) –уравнение прямой в пространстве проходящей через две заданные точки. X2 – X1 = k Y2 –Y1 = l Z2 – Z1 = m A(k; l; m) êêпрямой проходящей через М1 и М2. - 2) уравнение прямой проходящей через заданную точку М1 с заданным направляющим вектором.

Взаимное расположение прямых и плоскостей.Пусть дана плоскость Ax + By + Cz + D = 0 - 3) . Пусть дана прямая - 4).A(l; m; n)– направляющий вектор для прямой. Тогда A * n = êA ê* ên êsina. sina = 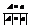= 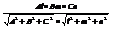- 5).Из 5)следует, что прямая 4) êê3), тогда угол a = 0 следует Al + Bm + Cn = 0 – условие параллельности прямой плоскости. Если 4) ^3), то a =90. 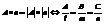- условие перпендикулярности прямой и плоскости.

21. Кривые второго порядка. Эллипс. Гипербола. Парабола.

Общее у-е кривых второго порядка: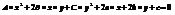

После изменения начала координат и переноса начала координат в новую т. или поворта координатных осей, кривые второго порядка могут быть преобразованы к более простому (каноническому) виду. В результате преобразований у-е может описывать следующие линии: эллипс; гиперболу; параболу; пару êêпрямых; пара пересекающихся прямых; точка.

Эллипс.

Эллипсом называют геометрическое место точек на плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и большая чем расстояние между фокусами.

Пусть задан эллипс F₁ и F₂ – фокусы эллипса, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F₁(c;0), F₂(-c,0), C>0.

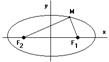
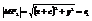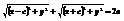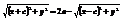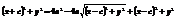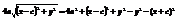
Пусть т. М лежит на эллипсе êMF₁ê+êMF₂ê=const =2a>2c Þ a>c , , r₁ и r₂ –фокальные радиусы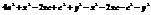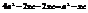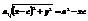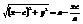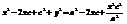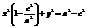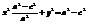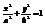. , , , , , , , , , , , , , - каноническое у-е эллипса.

Из канонического у-ия следует, что вместе с т. М лежащей на эллипсе, точки М₁(х;-у), М₂(-х;у), М₃(-х;-у) так же лежат на эллипсе, таким образом эллипс симметричен оси абсцисс и оси ординат. 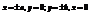- вершины.

Гиперболой называют геометрическое место точек на плоскости, модуль разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и меньшая чем расстояние между фокусами.

Пусть дана гипербола, F₁ и F₂ – фокусы гиперболы, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F₁(c;0), F₂(-c,0)

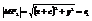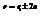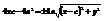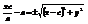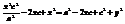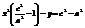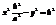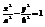, , , , , , , , , , , , , - каноническое у-е гиперболы.

Из канонического у-ия гиперболы получим , , 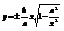ассимптоту гиперболы можно найти по формуле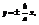

Параболой называют геометрическое место точек на плоскости, расстояние от которых до фиксированной точки, называемой фокусам, равно расстоянию до фиксированной прямой, называемой директрисой.

Выберем систему координат следующим образом, ось абсцисс проведём через фокус ^ директрисе, начало координат выберем посередине между фокусом и директрисой.

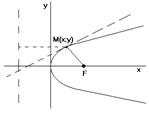
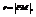тогда из определения - экцентрисситет.

Дата добавления: 2018-08-06; просмотров: 240; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!