Основные свойства определенного интеграла по отрезку (с доказательством одного из них)
1) 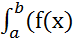 ±g(x))dx=
±g(x))dx= 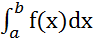 ±
± 
2) 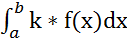 = k*
= k* 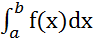 , гдеk-const
, гдеk-const
3) 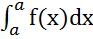 = 0
= 0
4) Если отрезок интегрирования [a,b] разбит на две части [a,c] и [c,b] то
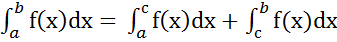 - свойство аддитивности.
- свойство аддитивности.
5) Если на [a,b]f(x)≥0, то 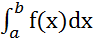 ≥0
≥0
6) Если на [a,b] f(x)≥g(x), то 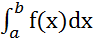 ≥
≥ 
7) 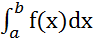 = -
= - 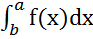
Доказать: 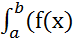 ±g(x))dx=
±g(x))dx= 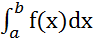 ±
± 
Доказательство: 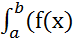 ±g(x))dx =
±g(x))dx =  (f(ξk) ±g(ξk))* ( xk - xk-1) =
(f(ξk) ±g(ξk))* ( xk - xk-1) =  (f(ξk)* ( xk - xk-1) ±g(ξk)* ( xk - xk-1)) =
(f(ξk)* ( xk - xk-1) ±g(ξk)* ( xk - xk-1)) = 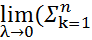 f(ξk)* ( xk - xk-1) ±
f(ξk)* ( xk - xk-1) ±  g(ξk)* ( xk - xk-1) =
g(ξk)* ( xk - xk-1) =  f(ξk)*( xk - xk-1) ±
f(ξk)*( xk - xk-1) ±  g(ξk)*( xk - xk-1) =
g(ξk)*( xk - xk-1) = 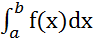 ±
± 
Теорема об оценке определенного интеграла по отрезку (формулировка, доказательство), геометрический смысл.
Если m – наим. значение функции f(x), M–наиб. значение функции f(x) на [a,b] ; (m ≤ f(x) ≤ M)
m(b-a) ≤ 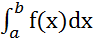 ≤ M(b-a)
≤ M(b-a)
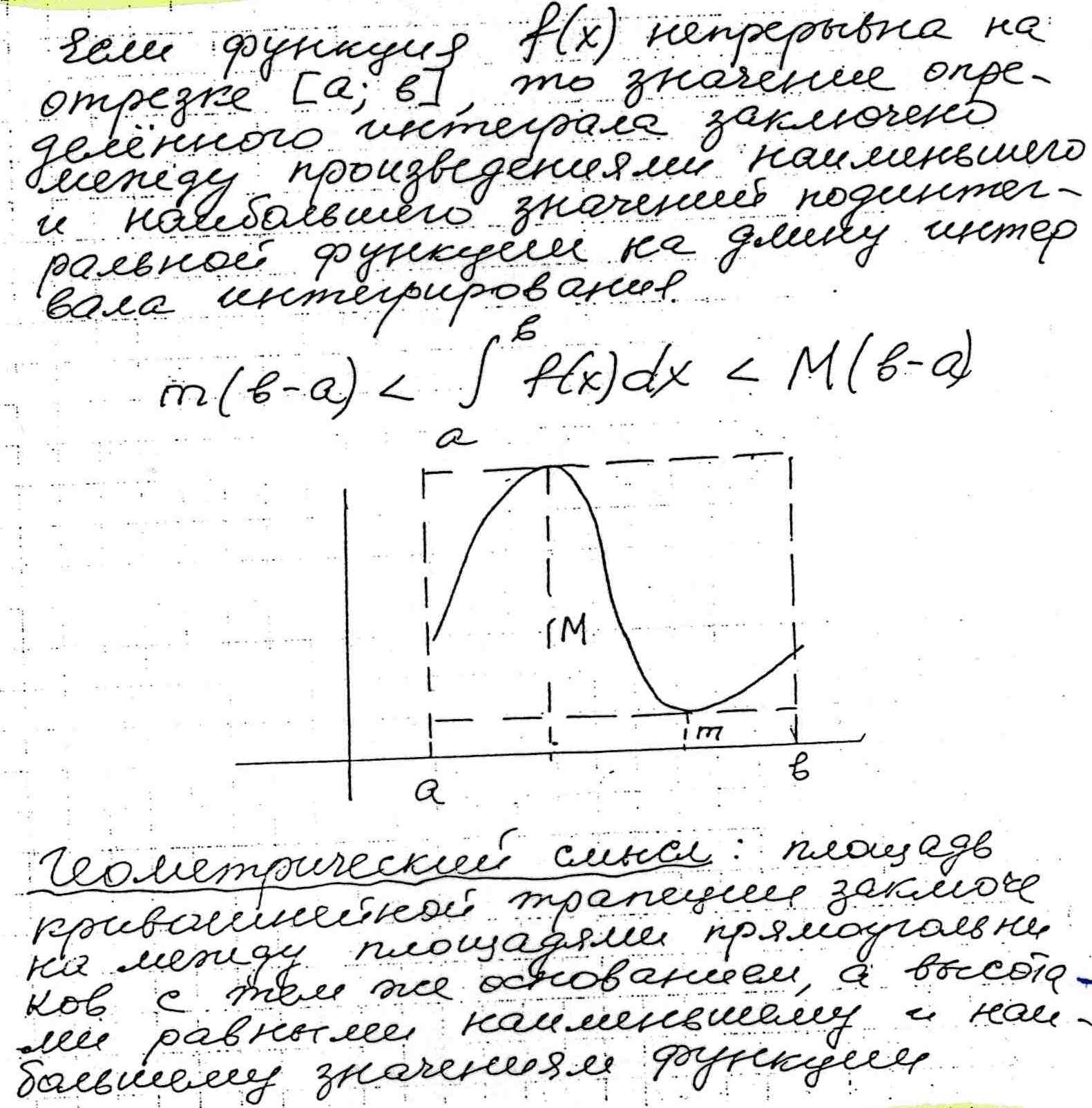 Площадь криволинейной трапеции не меньше площади прямоугольника с тем же основанием [a,b] и высотой, равной mи не больше площади прямоугольника с тем же основанием и высотой равной М.
Площадь криволинейной трапеции не меньше площади прямоугольника с тем же основанием [a,b] и высотой, равной mи не больше площади прямоугольника с тем же основанием и высотой равной М.
Дано: m ≤ f(x) ≤ M
Доказать: m(b-a) ≤ 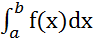 ≤ M(b-a)
≤ M(b-a)
Доказательство:
1) Пусть f(P) ≤ M, ∀P∈[a,b]
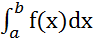 =
= 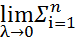 (Pi)*Δxi ≤
(Pi)*Δxi ≤ 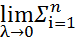 M*Δxi ≤M
M*Δxi ≤M 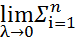 Δxi ≤ M*(b-a)
Δxi ≤ M*(b-a)
2) Пустьm ≤f(P), ∀P∈[a,b]
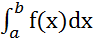 =
= 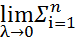 (Pi)*Δxi ≥
(Pi)*Δxi ≥ 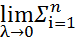 m*Δxi ≥ m*
m*Δxi ≥ m* 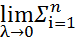 Δxi ≥ m*(b-a)
Δxi ≥ m*(b-a)
Теорема о среднем (формулировка, доказательство), геометрический смысл.
Средним значение функции f(x) на отрезке называется отношение значения определенного интеграла от этой функции по отрезку к длине этого отрезка:
Fсред. = 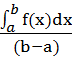
Теорема: Если функция f(x) непрерывна на отрезке [a,b], то существует хотя бы одна точка C∈ (a,b); что f(C) = fсред.
f(C) = 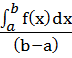 →
→ 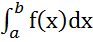 = f(C)*
= f(C)* 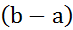
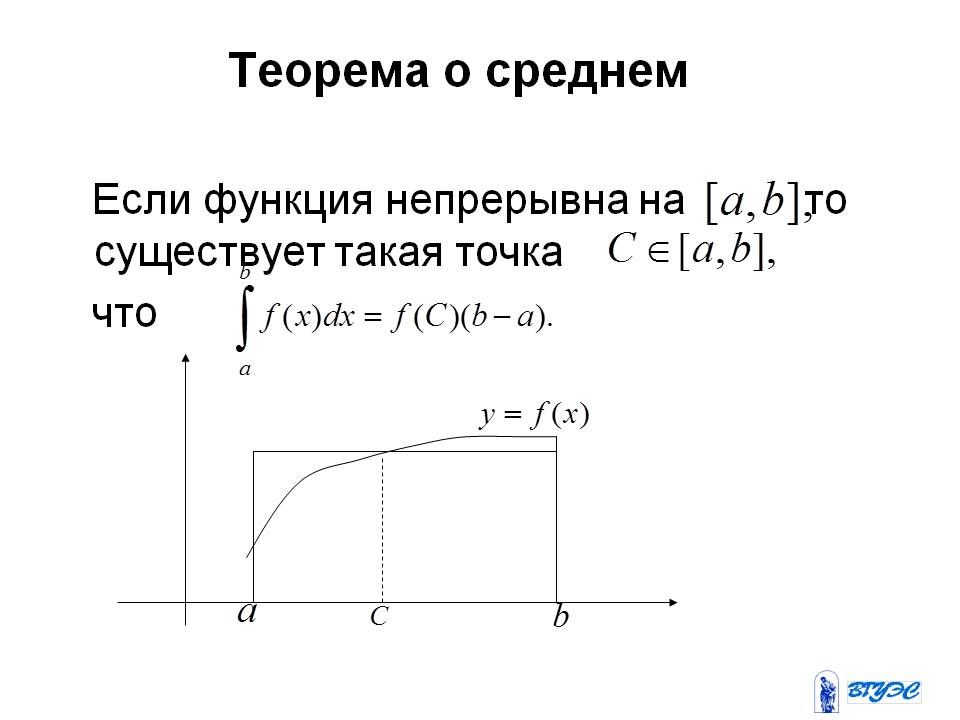 Криволинейная трапеция равновелика прямоугольнику с тем же основанием [a,b] и высотой равной f(C).
Криволинейная трапеция равновелика прямоугольнику с тем же основанием [a,b] и высотой равной f(C).
|
|
|
Дано: f(x) непрерывна на [a,b]
Доказать: ∃C∈ (a,b): f(C) = fсред.
Доказательство:
Так как f(x) непрерывна на [a,b], то m ≤ f(x) ≤ M
Тогда по теореме об оценке
m(b-a) ≤ 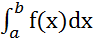 ≤ M(b-a)
≤ M(b-a)
m ≤ 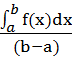 ≤ M , т.к. b-a≠ 0
≤ M , т.к. b-a≠ 0
m ≤ fсред≤ M
f(x) непрерывнана[a,b], значит, еслиm ≤ λ≤ M, то∃ C∈ (a,b): f(C) = λ→ f(C) = fсред
Интеграл с переменным верхним пределом.
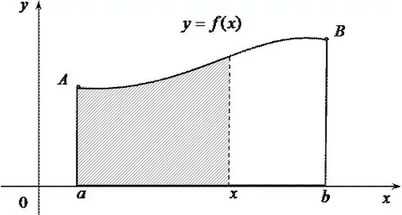 Пусть функция f интегрируема на [a; b]. Тогда по теореме о существования определенного интеграла функция f интегрируема на [a; x] для любого x ∈ [a; b]. Рассмотрим функцию F(x) =
Пусть функция f интегрируема на [a; b]. Тогда по теореме о существования определенного интеграла функция f интегрируема на [a; x] для любого x ∈ [a; b]. Рассмотрим функцию F(x) = 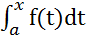 . Эта функция называется интегралом с переменным верхним пределом x.
. Эта функция называется интегралом с переменным верхним пределом x.
Теорема о производной интеграла с переменным верхним пределом (формулировка)
Производная интеграла с переменным верхним пределом от непрерывной функции равна подынтегральной функции, в которой переменная интегрирования заменена верхним пределом.
( 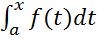 )’ = f(x)
)’ = f(x)
Определение дифференциального уравнения, его порядка, решения.
Диф. уравнением (ДУ)называется уравнение, связующее независимую переменную х, искомую функцию yи её производные, y’, y’’, y(n).
F(x , y , y’, y’’, … , y(n)) = 0
Порядком ДУназывают наивысший порядок производной, входящей в это уравнение.
|
|
|
Решением ДУназывается всякая функция y = f(x), которая будучи подставлена в это уравнение, превращает её в тождество.
Задача Коши для уравнения y’ = f(x,y) и её геометрический смысл.
Задача нахождения частного решения, удовлетворяющего данному начальному условию, называется задачей Коши для уравнения 1-го порядка.
y’ = f(x,y) ; y(x0) = y0
Геометрический смысл:
Найти ту интегральную кривую, которая проходит через данную точку.

Дата добавления: 2018-08-06; просмотров: 1569; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
