П.2. Интеграл с переменным верхним пределом интегрирования.
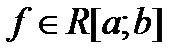
 (7)
(7)
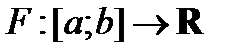 (корректно)
(корректно)
Теорема 3. Если 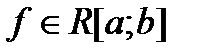 , то
, то 
Доказательство. 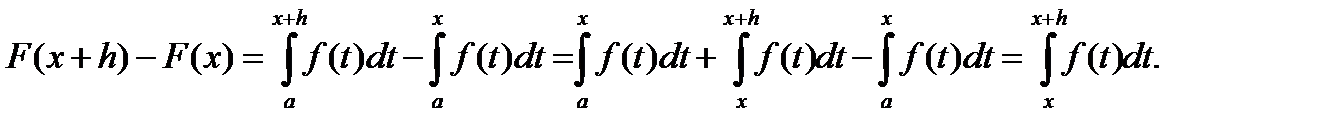
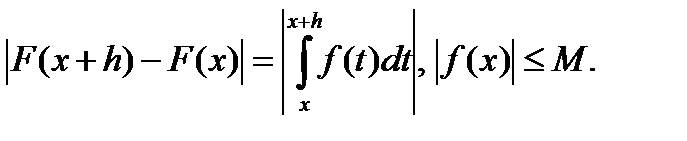 Значит
Значит 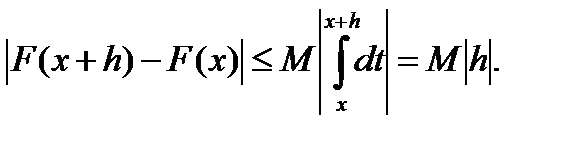
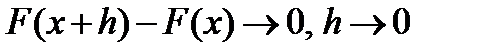
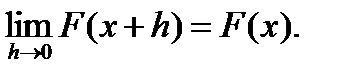
Теорема 4. Если 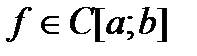 , то
, то 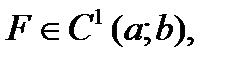 причём
причём
 (8)
(8)
Доказательство.
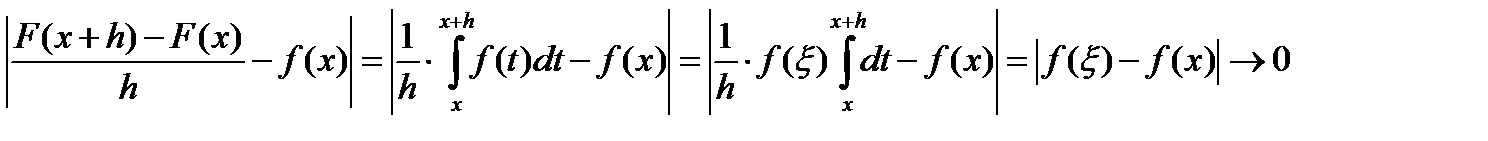 ,
,
при 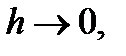
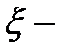 лежит между x и x + h,
лежит между x и x + h, 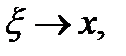 при
при 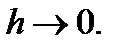
П.3. Формула Ньютона-Лейбница.
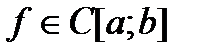 , тогда F – первообразная для f .
, тогда F – первообразная для f . 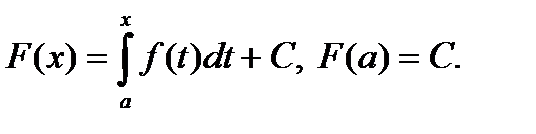
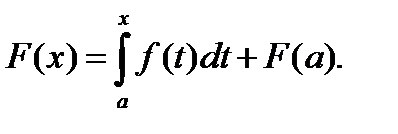 (9)
(9)

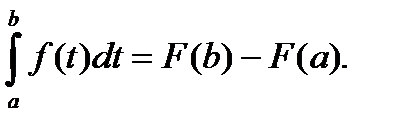
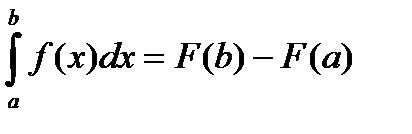 (10)
(10)
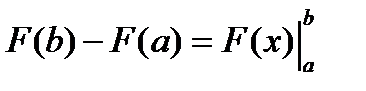
 (10.1)
(10.1)
П.3. Способ подстановки в интеграле, способ интегрирования по частям.
Теорема 5. Пусть f – непрерывна на 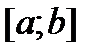 ,
, 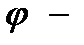 непрерывно дифференцируема на
непрерывно дифференцируема на 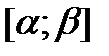 ,
, 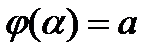 ,
,  F первообразная для f на
F первообразная для f на 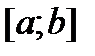 . Верна формула
. Верна формула
 (11)
(11)

Теорема 6.Пусть 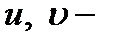 интегрируемы на [a; b]. Тогда
интегрируемы на [a; b]. Тогда
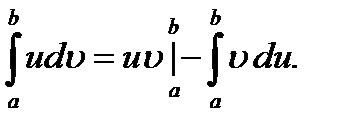 (12)
(12)
Критерий Дарбу.
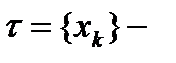 разбиение отрезка
разбиение отрезка 
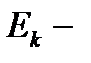 частичные отрезки.
частичные отрезки. 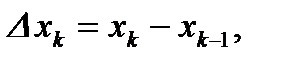
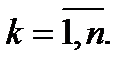

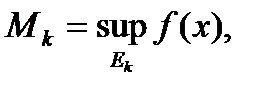
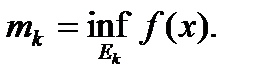
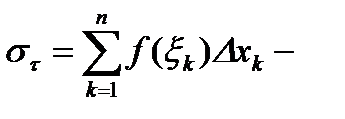 интегральная сумма;
интегральная сумма;
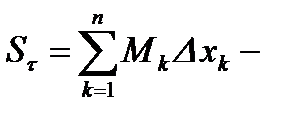 верхняя интегральная сумма Дарбу;
верхняя интегральная сумма Дарбу;
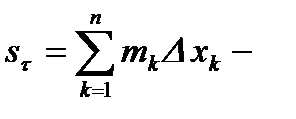 нижняя интегральная сумма Дарбу.
нижняя интегральная сумма Дарбу.
 (1)
(1)
Лемма. Пусть 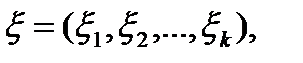
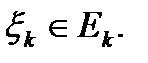 Тогда
Тогда 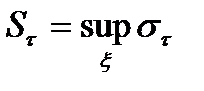 ,
, 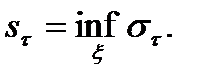
Доказательство. Очевидно,  Значит,
Значит, 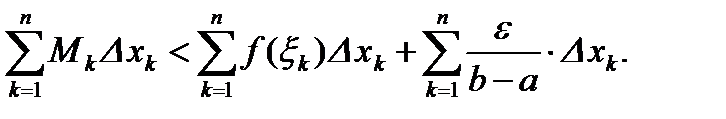
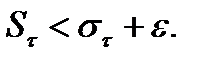 (2)
(2)
|
|
|
Аналогично можно показать, что 
Теорема. Для того чтобы ограниченная на 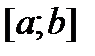 функция f была интегрируема на этом отрезке, необходимо и достаточно, чтобы
функция f была интегрируема на этом отрезке, необходимо и достаточно, чтобы
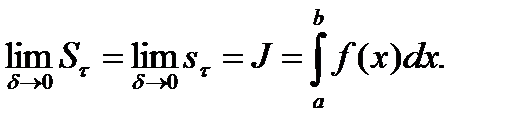
1) 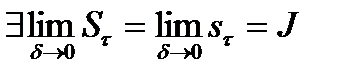 Из (1) следует, что
Из (1) следует, что 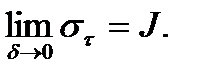
2) Пусть 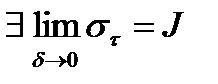 , учитывая (1) и (2) запишем
, учитывая (1) и (2) запишем 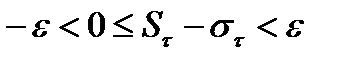 ,
, 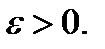 Значит
Значит 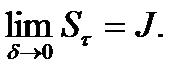
Аналогично можно показать, что 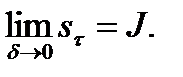
П.2. Об измеримых множествах.
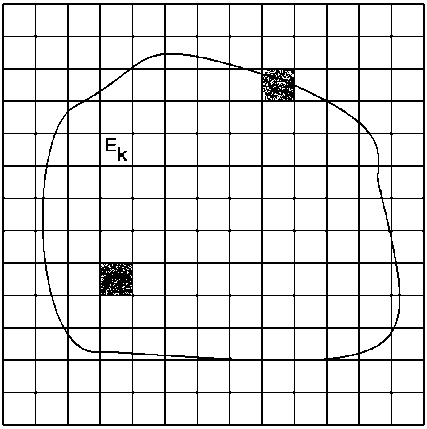
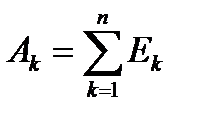 ,
, 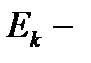 целиком входят в
целиком входят в 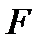 ,
, 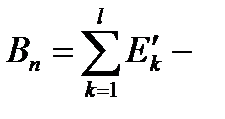 фигура
фигура 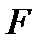 входит в объединение
входит в объединение 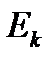 .
. 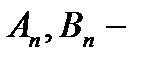 фигуры ранга n.
фигуры ранга n. 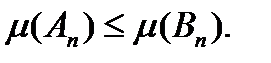 С увеличением ранга, очевидно, что
С увеличением ранга, очевидно, что 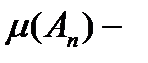 могут только увеличиваться, а
могут только увеличиваться, а 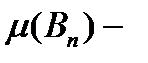 могут только уменьшаться.
могут только уменьшаться.
Определение.
1) 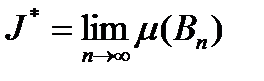 ,
, 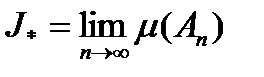 – называем верхней и нижней мерой Жардана множества F.
– называем верхней и нижней мерой Жардана множества F.
2) Если 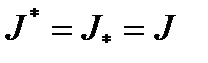 – конечные числа, то множество F называется измеримым (по Жардану), а значит
– конечные числа, то множество F называется измеримым (по Жардану), а значит 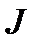 называется мерой Жардана множества F.
называется мерой Жардана множества F.
3) Будем считать 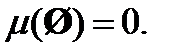
Приложение интегралов.
П.1. Длина дуги кривой.
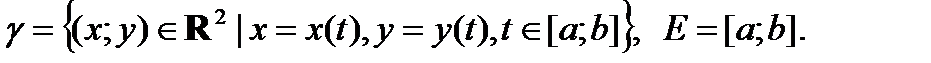 Будем считать, что
Будем считать, что 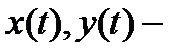 непрерывны по
непрерывны по 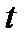 в
в 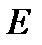 . Множество
. Множество 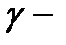 будем называть непрерывной кривой на плоскости.
будем называть непрерывной кривой на плоскости.
Если при 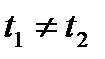 ,
, 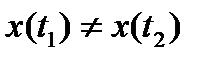 ,
, 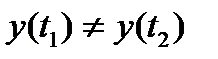 , то кривую
, то кривую 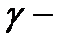 будем называть кривой без самопересечений.
будем называть кривой без самопересечений.  ,
, 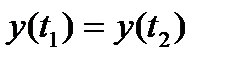 при
при 
 имеет самопересечения.
имеет самопересечения.
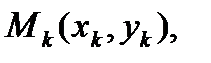
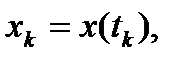
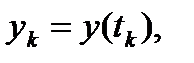
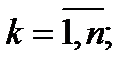

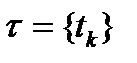
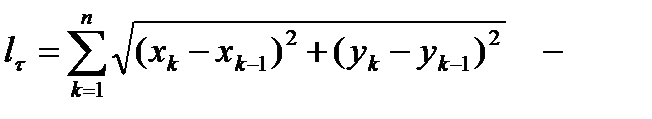 длина ломаной.
длина ломаной.
Считаем, 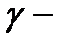 гладкая кривая! Значит
гладкая кривая! Значит  непрерывно дифференцируемые функции, причём
непрерывно дифференцируемые функции, причём 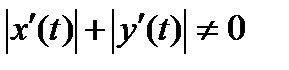 .
. 
|
|
|
Например.  ,
, 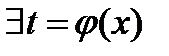 ,
, 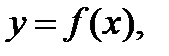
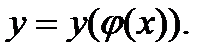
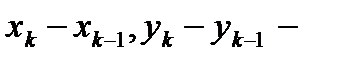 такие разности заменим по теореме Лагранжа, тогда
такие разности заменим по теореме Лагранжа, тогда
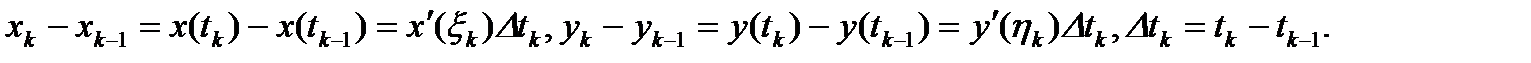
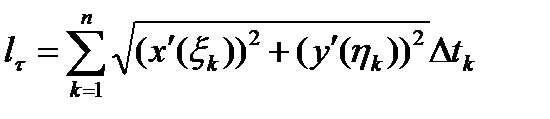 (1)
(1)
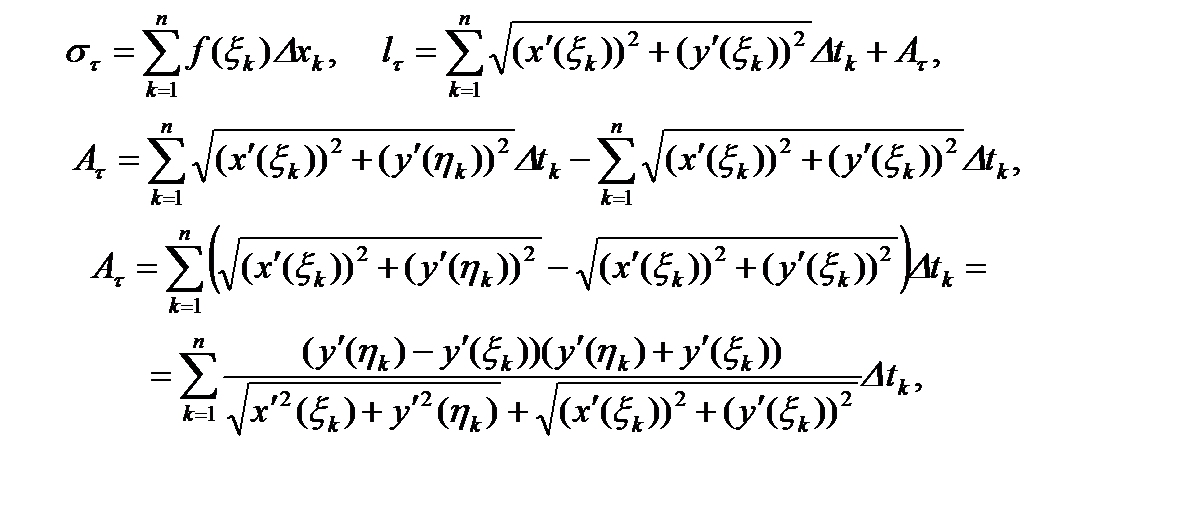
так как 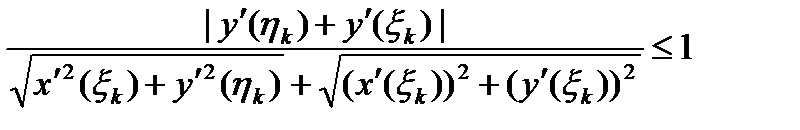 , то
, то
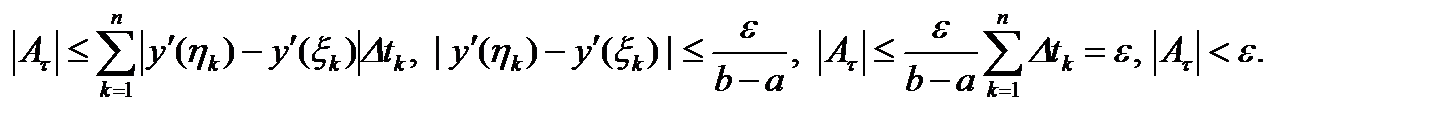
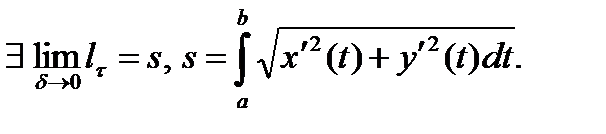
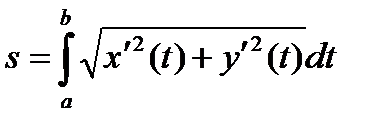 (2)
(2)
Определение. Если множество  для
для 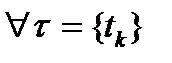 разбиения отрезка
разбиения отрезка 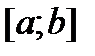 ограничено сверху, то кривую
ограничено сверху, то кривую 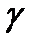 называют спрямляемой кривой. Число
называют спрямляемой кривой. Число 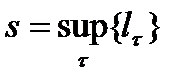 назовём длинной дуги кривой.
назовём длинной дуги кривой.
Так как с одной стороны при уменьшении 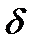 (диаметра разбиения) длины ломаных увеличиваются, то ясно, что
(диаметра разбиения) длины ломаных увеличиваются, то ясно, что 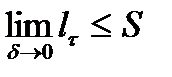 . С другой стороны, очевидно, что
. С другой стороны, очевидно, что  откуда
откуда  . Кривая задана уравнением
. Кривая задана уравнением 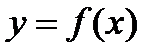
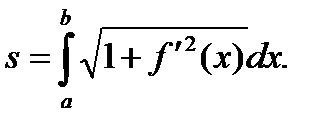
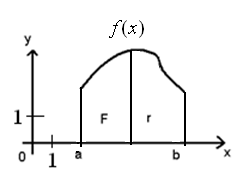
П.2. Площадь криволинейной трапеции. Площадь фигуры в полярных координатах.
 Пример.
Пример. 
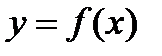 ,
, 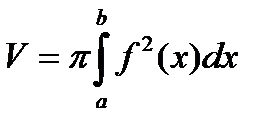 ,
, 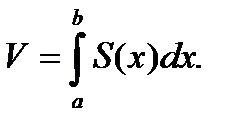
Площадь фигуры в полярных координатах.
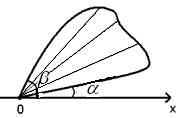
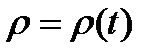 ,
, 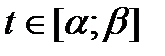 ,
, 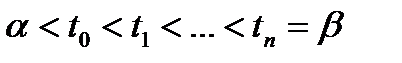 ,
, 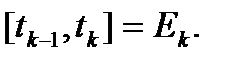
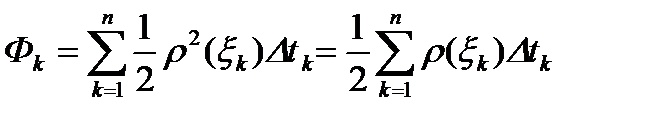 ,
,  ,
, 
П.3. Площадь поверхности вращения.
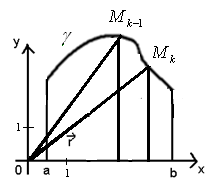
Мы имеем плоскость  и будем вращать её вокруг
и будем вращать её вокруг 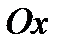 .
.
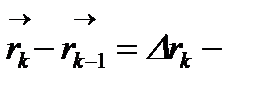 длина,
длина, 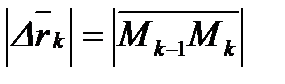
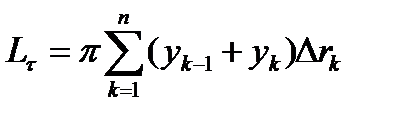 (4)
(4)
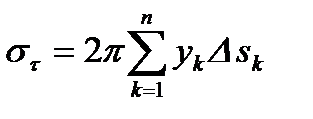 (5)
(5)
Кривая 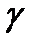 имеет длину
имеет длину  .
. 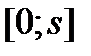
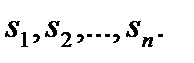 Покажем, что
Покажем, что
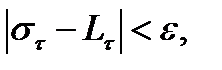
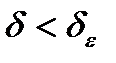 (*)
(*)
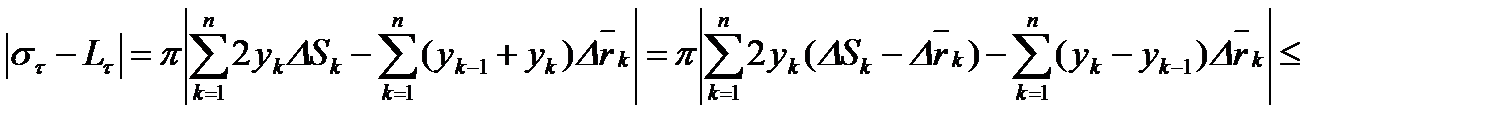
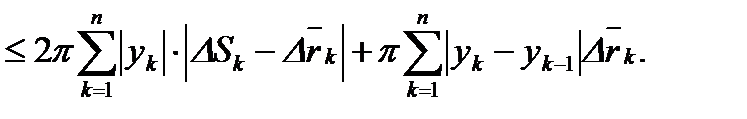
Положим 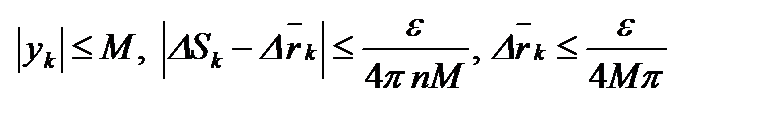 , тогда получим
, тогда получим
|
|
|
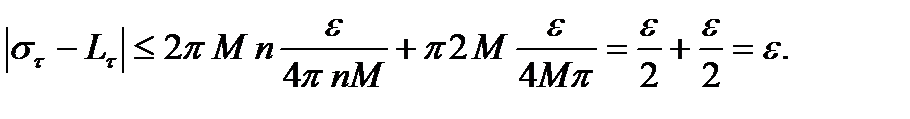
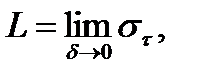
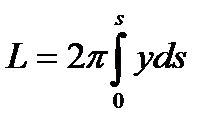
1) 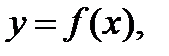
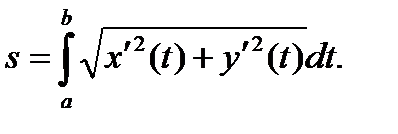
2) 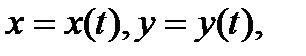
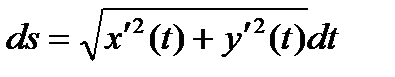
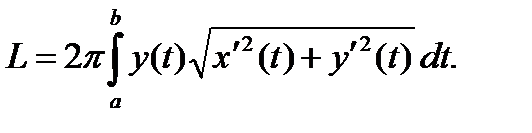 (6)
(6)
Формула (6) применяется для нахождения площади поверхности вращения.
П.4. Объем.
Дата добавления: 2018-08-06; просмотров: 201; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
