Основные методы интегрирования(опред. интеграл)
Тема 1 Математический анализ
1 Функции одной независимой переменной
Нахождение производной называется дифференцированием функции.Производная функции y=f(x) в точке 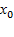 называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю.
называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю. 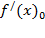 =
= 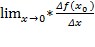
Чтобы функция f(x) была дифференцируема в точке 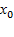 необходимо и достаточно, чтобы она имела в этой точке конечную производную(число). Если функция дифференцируема в данной точке, то она не прерывна в этой точке.
необходимо и достаточно, чтобы она имела в этой точке конечную производную(число). Если функция дифференцируема в данной точке, то она не прерывна в этой точке.
Задать функцию, значит задать три объекта:
1) множество Х (область определения функции);
2) множество Y (область значений функции);
3) правило соответствия f (сама функция).
2 Производная, её механический смысл
Производная используется для вычисления скорости и ускорения различный физических тел. Мгновенная скорость v (t) определена (только) для любой дифференцируемой функции x(t), при этом 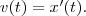 Производная от координаты по времени есть скорость.
Производная от координаты по времени есть скорость.
Мгновенная скорость может принимать как положительные, так и отрицательные значения и 0. Если скорость на каком-либо промежутке времени (t1; t2) положительна, то точка движется в положительном направлении, т. е. координата растет с течением времени, а если v (t) отрицательна, то координата х (t) убывает.
Коротко говорят: производная от скорости по времени есть ускорение. 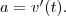
3 Правила дифференцирования. Формулы производных
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
|
|
|
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5) если y = f(u),
u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функцийj и f, то 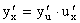 , или
, или 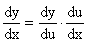 ;
;
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем  ≠ 0, то
≠ 0, то 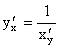 .
.
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u)' = u1 u' ( принадлежит R1 )
2. (au)' = au lna u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u u'.
7. (cos u)' = - sin u u'.
8. (tg u)' = 1/ cos2u u'.
9.(ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' / 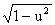 .
.
11. (arccos u)' = - u' / 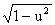 .
.
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
4 Производные и дифференциалы высших порядков
Пусть мы нашли для функции y = f(x) ее производную y '= f '(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается 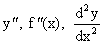 . Аналогично определяются и обозначаются: производная третьего порядка -
. Аналогично определяются и обозначаются: производная третьего порядка -  , производная четвертого порядка -
, производная четвертого порядка - 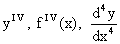 и вообще производная n-го порядка -
и вообще производная n-го порядка - 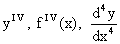 .
.
Частная производная функции u=f(x,y) это предел отношения частного приращения функции к приращению рассматриваемой независимой при условии, что последнее приращение стремится к нулю 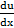 =
= 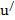 x;
x; 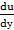 =
= 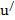 у;
у; 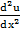
|
|
|
5 Геометрический смысл производной
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t0.
6 Приложения производной и дифференциала функции
- Формула Тейлора.
Приближение функции в окрестности точки 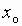 многочленом может быть удобно в работе с этой функцией.
многочленом может быть удобно в работе с этой функцией.
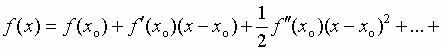
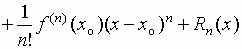 , где остаточный член
, где остаточный член 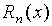 , например, в форме Лагранжа, имеет вид
, например, в форме Лагранжа, имеет вид 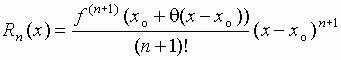 , где
, где 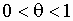 (вообще говоря,
(вообще говоря, 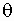 зависит от
зависит от 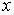 и
и 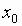 ).
).
Справедливы следующие формулы Маклорена (формулы Тейлора при 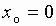 ) для некоторых элементарных функций:
) для некоторых элементарных функций:
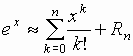 .;
.; 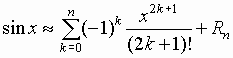
.
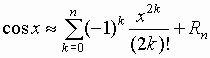 ;.
;. 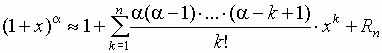
.
 ;.
;. 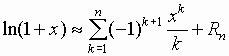
7 Исследование функции с помощью производной
Определение 1. Функция 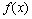 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке 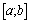 , если для любых
, если для любых  имеет место:
имеет место:
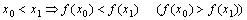 .
.
Теорема 1. Пусть 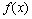 имеет производную в каждой точке из
имеет производную в каждой точке из 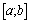 . Тогда
. Тогда 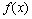 возрастает (убывает) на
возрастает (убывает) на 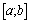 в том и только в том случае, когда для любого
в том и только в том случае, когда для любого 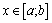
 .
.
|
|
|
Определение 2. Точка 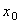 называется точкой максимума
называется точкой максимума 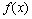 , если существует окрестность
, если существует окрестность 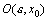 такая, что
такая, что 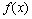 определена в этой окрестности и для любого
определена в этой окрестности и для любого 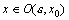
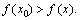 Определение 3. Точка
Определение 3. Точка 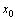 называется критической точкой функции
называется критической точкой функции 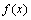 , если
, если 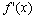 не определена в этой точке или
не определена в этой точке или  .
.
Теорема 2. 1) если 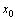 – точка экстремума функции
– точка экстремума функции 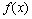 , то она является критической точкой этой функции;
, то она является критической точкой этой функции;
2) если 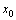 – критическая точка функции
– критическая точка функции 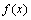 , причем для
, причем для 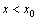

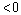 , a для
, a для 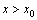

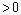 в некоторой окрестности
в некоторой окрестности 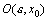 , то
, то 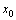 – точка минимума;
– точка минимума;
3) если 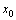 – критическая точка функции
– критическая точка функции 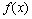 , причем для
, причем для 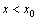
 >0, а для
>0, а для 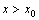
 <0 в некоторой окрестности
<0 в некоторой окрестности 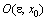 , то
, то 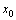 – точка максимума.
– точка максимума.
8 Функции нескольких переменных. Частные производные различных порядков
Область определения
Область определения функции нескольких переменных – некоторая область в плоскости XOY.
График функции двух переменных
Графиком функции двух переменных в декартовой прямоугольной системе координат в пространстве является поверхность, проектирующаяся на плоскость XOY в область определения функции.
Непрерывность функции двух переменных
Функция непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Если в некоторой точке не выполняется условие непрерывности функции, то эта точка -точка разрыва функции.
|
|
|
Если функция зависит не от одного, а от нескольких аргументов xi (iизменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… xn), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, xi . Частная производная 1-ого порядка по xi определяется как обычная производная, при этом предполагается, что все аргументы, кроме xi, сохраняют постоянные значения. Для частных производных вводятся обозначения
fxn, или 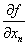
9 Определение и свойства неопределённого интеграла
Функция 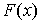 называется первообразной функции
называется первообразной функции 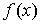 , если выполняется равенство
, если выполняется равенство 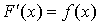 . Функция, производная которой на некотором промежутке F(х)=0 постоянна на этом промежутке. Если
. Функция, производная которой на некотором промежутке F(х)=0 постоянна на этом промежутке. Если 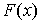 - одна из первообразных функции
- одна из первообразных функции 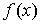 , то любая другая первообразная имеет вид
, то любая другая первообразная имеет вид  .
.
Свойства:
1.Деференциал неопред.интеграла = подинтегральному выражению, производная = подинтегральной функции d 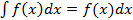 ; (
; ( 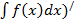 =f(x);
=f(x);
2.Алгебраическая сумма функций = алгеб.сумме неопред. интегралов этих функций.
3. Подинтегральный множитель выражения можно выполнить под знак интеграла 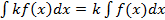
10 Определение и свойства определённого интеграла. Формула Ньютона-Лейбница
Определенным интегралом f(x) на отрезке [a,b] назыв. Предел интегральной функции при условии, что длина наибольшего из отрезков стремится =0.
Свойства:
1. Формула Ньютона-Лейбница 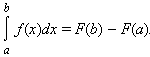 если а=b, то интеграл =0
если а=b, то интеграл =0
2. Если a>b то  = -
= - 
3. Если a b любые числа то 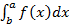 =
= 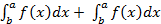
4. Постоянный множитель можно вынести 
5. Определенный интеграл алгебр. суммы функции=алгебр. сумме их интегралов
11 Основные методы интегрирования(неопред. интеграл)
1. С помощью таблицы интегралов
2. Метод подстановки с помощью введения новой переменной
 | x=¥(t) |
| x=¥(t) |  (t)dt
(t)dt
3. Метод интегрирования по частям
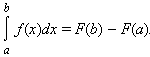
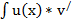 (x)dx=u(x)
(x)dx=u(x)  v(x) -
v(x) - 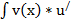 (x)dx
(x)dx
Основные методы интегрирования(опред. интеграл)
1. С помощью формулы Ньютона-Лейбница
2. Метод подстановки с помощью введения новой переменной
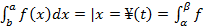 (¥(t))*
(¥(t))*  (t)dt
(t)dt
3. Метод интегрирования по частям
 -
- 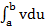
12 Геометрический смысл определенного интеграла
Если f(x) непрерывна и положительна на [a, b], то интеграл

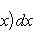
представляет собой площадь криволинейной трапеции, ограниченной линиями
y = 0, x = a, x = b, y = f(x)
13 Приложения определённого интеграла
1.Площадь криволинейной трапеции Sтр.= 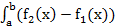 dx
dx
2. Объем тела вращения V= 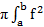 (x)dx S=2
(x)dx S=2 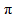
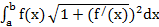
Дата добавления: 2018-08-06; просмотров: 187; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
