Овражные методы (Метод Гельфанда)
Вторая эвристическая схема, предложенная И.М. Гельфандом, состоит в следующем.
| |
Пусть х0 и - две произвольные близкие точки. Из х0 совершают обычный градиентный спуск с постоянным шагом и после нескольких итераций с малым шагом a попадем в точку u0. Тоже самое делаем для точки , получая точку . Две точки u, лежат в окрестности «дна оврага». Соединяя их прямой, делаем «большой шаг» l в полученном направлении, перемещаясь «вдоль дна оврага» (шаг l называют овражным шагом). В результате получаем точку х1. В ее окрестности выбираем точку и повторяем процедуру.
Схема овражного метода 1.
Шаг 1. Вводятся начальное приближение х0, точность решения e1 и e3, шаг a для
градиентного спуска, начальное значение l для овражного шага. Из точки х0
осуществляется градиентный спуск с постоянным шагом a на дно оврага. В
результате получается точка u0. Полагается к=0.
Шаг 2. В окрестности хк берется точка и из нее осуществляется градиентный
спуск. В результате получается точка .
Шаг 3. Новая точка хк+1 определяется следующим образом. По формуле
или
 |
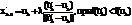вычисляется точка x'k+1. Из нее осуществляется градиентный спуск и мы получаем точку u`(xk+1) . Если f(u`(xk+1))<f(uk), то полагаем xk+1= x`k+1 и uk+1= u`k+1.
Иначе уменьшаем овражный шаг l (например в 2 раза l=l/2)и повторяем шаг 3.
Шаг 4. Если ||uk+1-uk||£e1 и || f `(uk+1) ||£e3, то полагаем:
 |
|
|
|
 |
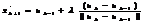и поиск минимума на этом заканчивается, иначе к=к+1 и переходим к шагу 2.
Рассмотрим другую реализацию той же идеи.
Пусть х0 и х1 – две произвольные близкие точки. Как и в предыдущем случае, из каждой точки осуществим градиентные спуски с постоянным шагом a. Получим точки u0 и u1, лежащие в окрестности «дна оврага». Соединяя их прямой, делаем «большой шаг» l в полученном направлении. В результате получим точку х2. Из этой точки осуществим градиентный спуск и получим точку u2. А вот далее, для того чтобы осуществить «овражный шаг», берем предпоследнюю точку u1. Соединяя прямой точки u2 и u1, делаем шаг l в полученном направлении и определяем х3. Дальше аналогичным образом вычисляются х4,х5, … .
| |
Схема овражного метода 2
Шаг 1. Задаются начальное приближение х0, точность решения e1 и e3, шаг a для градиентного спуска, начальное значение l для овражного шага.
Из точки х0 осуществляется градиентный спуск с постоянным шагом a на «дно оврага». В результате получается точка u’0.
В окрестности х0 берется точка х1, из которой тоже осуществляется градиентный спуск на «дно оврага». В результате получается точка u’1. Полагается к=1. Если f(u’0)<f(u’1), то полагаем u0=u’1, u1=u’0. Если f(u’0)>f(u’1), то u0=u’0, u1=u’1.
|
|
|
Шаг 2. Новая точка хк+1 определяется следующим образом. По формуле:
вычисляется точка x'k+1. Из нее осуществляется градиентный спуск и мы получаем точку u`k+1 . Если f(u`k+1)<f(uk), то полагаем xk+1= x`k+1 и uk+1= u`k+1.
Иначе уменьшаем овражный шаг l (например в 2 раза l=l/2)и повторяем шаг 2.
Шаг 3.
Если ||uk+1-uk||£e1 и | f `(uk+1) ||£e3, то полагаем:
и поиск минимума на этом заканчивается, иначе к=к+1 и переходим к шагу 2.
Дата добавления: 2018-08-06; просмотров: 968; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!