Сравнение с квадратурными формулами
Рассмотрим следующую квадратурную формулу для двойного интеграла:
 (51)
(51)
где gi,k –веса. Допустим, что погрешность этой формулы ведет себя приблизительно как C1N-m,
где C1 – некоторая const.;
ε > 0 – заданная точность вычисления интеграла.
Полагая C1N-m» ε, находим требуемое N » C2е-1/m, (C2 – некоторая const) следовательно, число Nf вычисляемых значений функции f в квадратурной формулы в n - мерном случае зависит от ε следующим образом:
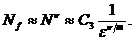 (C3 – некоторая const)
(C3 – некоторая const)
В методе Монте – Карло должно быть 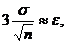 то есть для достижения той же точности вероятностью, близкой к единице, метод Монте–Карло требует вычисления
то есть для достижения той же точности вероятностью, близкой к единице, метод Монте–Карло требует вычисления 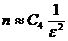 (где C4 – некоторая const) значений функции f независимо от размерности n. Например, при n = 15, m = 3 имеем
(где C4 – некоторая const) значений функции f независимо от размерности n. Например, при n = 15, m = 3 имеем
 (C4 – некоторая const)
(C4 – некоторая const)
Таким образом, в многомерном случае при применении метода Монте –Карло число вычисляемы значений подынтегральной функции растет значительно медленнее относительно 1/ε (ε – точность вычисления интеграла), чем в квадратурных формулах. Это свойство выражает первое преимущество метода Монте – Карло.
Второе преимущество метода Монте – Карло состоит в том, что его точность не зависит от гладкости подынтегральной функции.
Третье преимущество – простая приспособляемость к форме области интегрирования.
Например, полагаем

где R – квадрат, содержащий заданную область W (см.рис.) 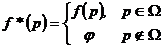
|
|
|
Далее применяется формула вида (50).
Недостатком метода Монте – Карло является вероятный характер результата, то есть отсутствие строгих, стремящихся к нулю при n→¥ оценок погрешности.
Замечание. Метод Монте – Карло и другие методы интегрирования, подобные рассматриваемому, где приближенное значение интеграла зависит от некоторых случайных параметров, называются недетерминированными.
Метод неопределенных коэффициентов
Трудоемкость решения задач резко возрастает с ростом их размерности, и поэтому, как правило, не удается разработать стандартные методы решения широких классов многомерных задач со столь же высокой точностью, как в одномерном случае. Хотя значительная часть результатов теоретических исследований для одномерного случая может быть перенесена на случай функций двух и более переменных.
Несколько утешает следующее обстоятельство. Многомерные математические задачи обычно возникают из описания сложных процессов. Обычно уже эти описания являются довольно грубыми, и поэтому значительно реже предъявляется требование решения этих задач с такой же высокой точностью, как в одномерном случае.
Решение ряда многомерных задач часто сводится к решению следующих элементарных задач.
|
|
|
Пусть в некоторой области S – мерного пространства G заданы точки P1, P2, …, PN и значения функции f в этих точках. Требуется:
1) получить приближения к значению функции f(p);
2) получить приближение к значению некоторой производной Df функции в точке P;
3) вычислить интеграл 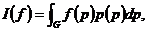 где p(p) - некоторая весовая функция.
где p(p) - некоторая весовая функция.
Простейшим способом решения этих задач является метод неопределенных коэффициентов.
Пусть из каких-то соображений известно, что функция f(p) хорошо приближается линейными комбинациями вида 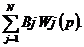
Потребуем, чтобы такая линейная комбинация совпадала с f(p) в заданных узлах, то есть выполнялись равенства
 (52)
(52)
Предположим, что det // Wj(Pg) // ¹ 0 , тогда матрица // Wj(Pg) // имеет обратную A = // aij //, и решение системы (52) записывается в виде
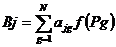 (53)
(53)
Функция  совпадает с функцией f(p) в точках P(g). Подставляя в предыдущее соотношение Bj из (53), получим иное представление g(p), а именно:
совпадает с функцией f(p) в точках P(g). Подставляя в предыдущее соотношение Bj из (53), получим иное представление g(p), а именно:
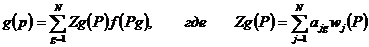 (54)
(54)
Такая форма записи интерполяционной функции является аналогом записи интерполяционного многочлена в форме Лагранжа. Как и в одномерном случае, можно надеяться, что при удачном выборе узлов Pg и функций Wj(P) будет мала погрешность в приближенных равенствах:
|
|
|
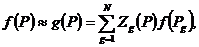 (55)
(55)
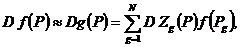 (56)
(56)
 (57)
(57)
При неудачном выборе большого числа узлов интегрирования погрешность приближенного равенства (55) может оказаться очень большой. Поскольку приближенные равенства (56), (57) являются следствием (55), то может быть большой и погрешность в приближенных равенствах (56), (57). Поэтому применение соотношений (55)-(57) требует основания и выяснения условий законности использования.
Дата добавления: 2018-06-27; просмотров: 258; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
