Решение нелинейных уравнений и систем нелинейных уравнений.
Для решения нелинейных уравнений могут быть использованы следующие процедуры Mathcad:
- root;
- вычислительный блок Given-Find(Дано - Найти);
- вычислительный блок Given-Minerr(Дано - Минимальная погрешность).
Особенности применения процедуры rootприведены в разделе алгебраических уравнений. Рассмотрим применение вычислительных блоков. Пусть дана система нелинейных уравнений:
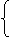x3+sin(y)=25
y2-cos(x)=27
Продемонстрируем решение этой системы в пакете Mathcad:
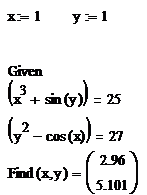
При использовании вычислительного блока необходимо учитывать следующие особенности:
1. Должны быть определены начальные приближения к корням (в данном примере x:=1 y:=1).
2. В равенствах должны быть использованы знаки тождественного равенства (жирное равенство с Палитры отношений и логики). Кроме равенств система может включать и неравенства, образуемые знаками <, >, ³, £.
3. Служебные слова Given, Find могут быть взяты из служебных слов, либо просто напечатаны.
Вычислительный блок Given – Find создает итерационную последовательность приближений к корню, начиная с заданного начального приближения. Полученное решение таково, что при подстановке его в уравнение правая и левая часть его отличается на величину TOL(TOLerance – точность, погрешность). По умолчанию величина TOL=10-3 . Если требуется более точный результат, то величину TOL можно сменить либо в меню MATH®Options, либо задав величину в рабочем листе, например: TOL :=10-8. (Имя переменной TOL записывается только в верхнем регистре).
|
|
|
Правила записи вычислительного блока Given – Minerrтакие же. Однако итерационная процедура поиска корней ориентирована на поиск решения, минимизирующего разность правой и левой части уравнений. Поэтому возможны ситуации, когда при одних и тех же начальных приближениях вычислительные блоки Given – MinerrиGiven – Findприводят к разным решениям.
Решение дифференциальных уравнений.
Будем рассматривать обыкновенное дифференциальное уравнение (ОДУ), содержащее одну независимую переменную и производные по ней. ОДУ имеют множество решений. Для отыскания единственного решения необходимы дополнительные условия. Если дополнительные условия заданы при одном значении независимой переменной x, то условия называются начальными. Количество начальных условий соответствует порядку дифференциального уравнения.
Пусть задано обыкновенное дифференциальное уравнение 1-го порядка с начальным условием:
y’(x)=f(x, y),
y(a)=y0
Требуется найти функцию y(x), при xÎ[a, b]. Данная задача носит название задачи Коши. Общий метод численного решения задачи Коши – метод Рунге-Кутта. В этом методе интервал [a, b] разбивается на n частей. Приближенное значение функции y(xi) возможно найти лишь в этих внутренних точках интервала, т.е. на сетке узлов xi : a=x0<x1<x2<…<xi<…<xn=b.
|
|
|
| X0 | X1 | X2 | … | Xi | … | Xn |
| Y0 | Y1 | Y2 | … | Yi | … | Yn |
xi =xi-1+h, i=1,2,…n.
h=(b-a)/n
В пакете Mathcad существует несколько процедур решения задачи Коши. Основные из них следующие:
- Rkfixed;
- Rcadapt;
- Bulstoer.
Описание процедуры Rkfixed(y, a, b, n, D).
Параметры процедуры:
y – вектор начальных значений. Размерность вектора y соответствует порядку дифференциального уравнения (т.е. для уравнения 1-го порядка вектор y содержит лишь одно значение).
a, b – начало и конец интервала определения функции.
n – число точек разбиения интервала [a, b].
D – вектор первых производных, т.е. правая часть дифференциального уравнения с начальными значениями неизвестной функции. Размерность соответствует порядку дифференциального уравнения.
Процедура Rkfixed использует численный метод Рунге-Кутта четвертого порядка. Рассмотрим более подробно использование процедуры Rkfixed на примере.
y’=xy+0.1y2
При заданном начальном условии y(0)=0,5.
Требуется найти неизвестную функцию y(x), при xÎ[a, b].
Причем число разбиений интервала [a, b] n=10.
|
|
|
Так как имеем дифференциальное уравнение 1-го порядка, вектора y и D – одномерные. Напоминаем, что нумерация векторов в пакете Mathcad начинается с нуля. Ниже приведен фрагмент решения этого дифференциального уравнения в пакете Mathcad.
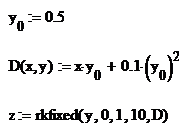
Переменная z представляет собой матрицу-результат, состоящую из двух столбцов. Первый столбец с индексом 0 содержит n+1 значение аргумента x, второй столбец – значение искомой функции y(x), вычисленные при соответствующих значениях аргумента. Следующий фрагмент программы Mathcad демонстрирует оформление результатов решения.
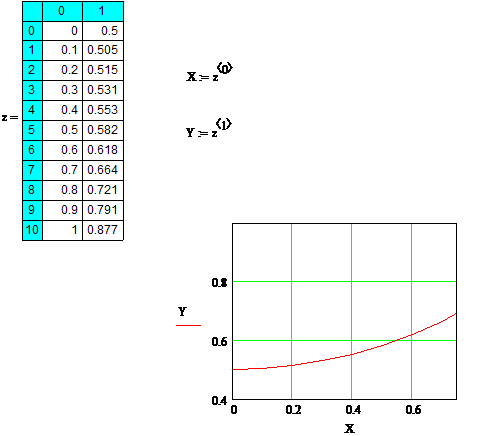
Процедура Rkfixed использует метод Рунге-Кутту с фиксированным (постоянным) шагом. Это не самый быстрый метод, но достаточно универсальный к виду интегрируемой функции. Если известно, что искомая функция быстро меняется, то целесообразно использовать процедуру Rkadapt, реализующую метод Рунге-Кутта с переменным (адаптивным) шагом. При этом переменный шаг используется только при нахождении функции y(x). При выводе результатов – шаг постоянный.
И, наконец, процедура Bulstoer использует более точный метод Булириш-Штёра. Этот метод весьма эффективен в случае гладких, медленно меняющихся функций. Параметры процедур Rkadapt и Bulstoer аналогичны Rkfixed.
|
|
|
Более общим случаем является обыкновенное дифференциальное уравнение n-го порядка. Задача Коши в этом случае содержит само дифференциальное уравнение с производными до n-го порядка включительно и n начальных условий. Решение дифференциального уравнения n-го порядка сводится к решению систем nдифференциальных уравнений 1-гопорядка. Рассмотрим методику этого метода на примере дифференциального уравнения 2-го порядка.
f ’’(x)=3f ’(x)+e5x
Требуется найти функцию f(x) при xÎ[0, 1]и начальных условиях:
f(0)=5,5;
f ’(0)=0.8.
Введем следующие обозначения:
 |
f(x)=f0(x),
f ’(x)=f1(x).
Продифференцируем левую и правую части последней системы.
f ’(x)=[f0(x)]’
f ’’(x)=[f1(x)]’
Или с учетом введенных обозначений и исходного дифференциального уравнения:
 |
[f 0(x)]’=f1(x)
[f 1(x)]’=3f1(x)+e5x
При начальных условиях
f 0(0)=5.5
f 1(0)=0.8
Получили систему двух дифференциальных уравнений 2-го порядка. Эта система в пакете Mathcad может быть решена с помощью любой процедуры, приведенной выше для одного дифференциального уравнения. Ниже приведен фрагмент решения этой системы в пакете Mathcad.
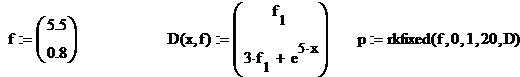
Оформление результатов решения также аналогично, с той лишь разницей, что матрица решения p содержит три столбца.
Третий столбик матрицы p содержит значения первых производных функции f(x).
Приближение функций.
Различают три задачи приближения экспериментальной информации (данных).
Интерполяция данных: требуется построить функцию, которая как можно ближе проходит через все значения экспериментальных данных. Иногда под интерполяцией понимают получение данных в промежутках между узлами [xi, xi+1].
В пакете Mathcad существует несколько процедур интерполяции экспериментальных данных многочленами различной степени. Процедуры lspline, pspline, cspline позволяют получить коэффициенты сплайн функции 1-го, 2-го и 3-го порядков соответственно. Эти коэффициенты являются затем входной информацией процедуры interp, производящей интерполяцию между узловыми значениями.
Пример совместного использования процедур:
Здесь x, y – векторные значения аргумента и функции экспериментальных данных; z – новые значения аргумента, по которым проводится интерполяция. Размерность вектора z, как правило, намного больше, чем размерность исходного вектора x.
Сглаживание данных: получение функции, устраняющей случайные погрешности, попавшие в экспериментальные данные.
Сглаживание данных возможно в двух вариантах: получение аналитической функции (регрессионного уравнения), позволяющей строить функцию при любых значениях аргумента, и получение нового набора значений функции, более гладких, чем исходные данные, но только при исходных значениях аргумента.
Регрессионная функция является оптимальной в среднеквадратическом смысле. Графически это свойство соответствует построению линии визуально усредняющей экспериментальные данные.
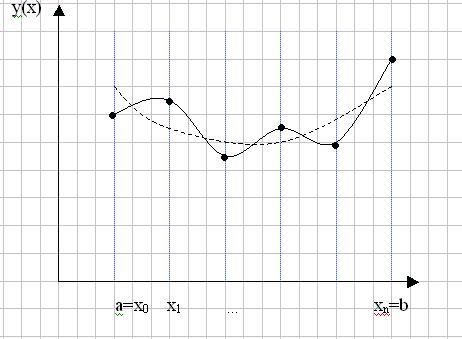
На рисунке точками (·) показаны экспериментальные данные, сплошной линией – функция их соединяющая, пунктирной – линия регрессии.
В пакете Mathcad для получения регрессионного уравнения предназначена процедура regress(x, y, k). Параметры процедуры:
x, y – векторные значения аргумента и функции экспериментальных данных;
k – порядок полинома.
Построим регрессионное уравнение 2-го порядка, предполагая, что векторные значения x, y заданы в пяти дискретных точках.
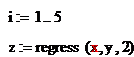
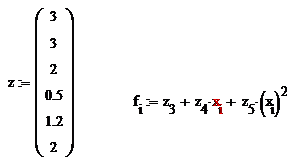
Первые две переменные вектора z: z0, z1, содержат служебную информацию, z2 – степень полинома, z3, z4, z5 – коэффициенты полинома. Вектор fсодержит значения сглаживающего полинома в пяти дискретных точках. Для получения большего числа значений полинома на том же интервале можно задать другую систему узлов с большим количеством, например, зададим 100 узлов.
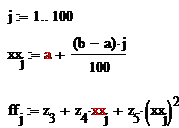
Если требуется получить непрерывную функцию, то регрессионное уравнение записывается так:
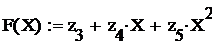
Здесь прописные буквы X, F введены для отличия от уже использованных векторных значений x, f.
Для получения сглаживания в виде набора значений в пакете Mathcad предназначены процедуры
- medsmooth;
- ksmooth;
- supsmooth.
Процедура medsmooth(y, k) позволяет получить значения функции, сглаженные с помощью скользящей медианы. Параметры процедуры:
y – вектор исходных данных (значения функции);
k – ширина окна, по которому происходит сглаживание.
Результатом работы оператора Mathcad
является вектор z, содержащий сглаженные значения. Размерность вектора z совпадает с размерностью вектора y.
Экстраполяция (прогноз) данных: предсказание значений функции вне интервала наблюдения. Как правило, требуется предсказать поведение функции в будущие моменты времени.
В пакете Mathcad для получения прогноза (в виде отдельных значений функции) предназначена процедура predict(y, n, m).
Параметры процедуры:
y – вектор значений экспериментальных данных;
n – глубина предыстории, т.е. сколько последних значений функции учитывается для прогноза;
m – количество прогнозируемых значений.
Рассмотрим использование процедуры predict для прогнозирования значений функции ln(x+1). Предполагаем, что для анализа приведены 50 значений функции (индекс i), прогноз проводится также на 50 точек (индекс k). Глубина предыстории – 5 точек.
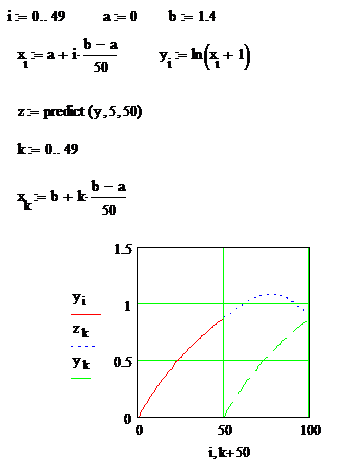
На графике сплошной линией приведена исходная функция и на интервале наблюдения, и на интервале прогноза, пунктирной линией – вектор прогнозируемых значений z. Как видно из графика, прогноз эффективен лишь на короткие интервалы. После 25-го значения вектора z становится принципиально различной динамика процессов.
Дата добавления: 2018-06-01; просмотров: 240; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!