Постановка общей задачи математического программирования. Основные понятия

⇐ ПредыдущаяСтр 4 из 22Следующая ⇒

Задачу линейного программирования нередко формулируют как задачу минимизации или максимизации линейной формы L=c₁x₁+c₂x₂+...c_nx_n (1) при ограничениях x₁≥0, x₂≥0, ...x_n≥0 и

∑ a_ijx_j≤b_i, i=1,2,...m₁,

∑ a_ijx_j=b_i, i= m₁+1, m₁+2,...m₂,

∑ a_ijx_j≥b_i, i= m₂+1, m₂+2,...m.

Такую запись называют общей задачей линейного программирования.

Обозначим через А матрицу системы линейных уравнений:

а₁₁x₁ + a₁₂x₂ + … a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + … a_2nx_n = b₂(2)

А = . . . . .

а_m1x₁ + a_m2x₂ + … a_mnx_n = b_m.

Через X и B – матрицы-столбцы (векторы) неизвестных и свободных членов:

, ,

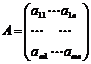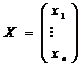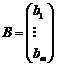
а также введем в рассмотрение n-мерный вектор C = (с₁ … с_n), компонентами которого служат коэффициенты линейной формы (1), и n-мерный нуль-вектор 0(0, 0, …, 0). Тогда линейную форму можно рассматривать как скалярное произведение L=CX (3), систему линейных уравнений (2) заменить одним матричным уравнением AX=B (4), а условия x₁≥0, x₂≥0, ...x_n≥0 записать в виде X≥0(5). Поэтому часто основную задачу линейного программирования кратко записывают как задачу минимизации(максимизации) линейной формы (3) при линейных ограничениях (4) и (5).

Вектор-градиент, линия уровня, область допустимых решений в задаче ЛП. Геометрическая интерпретация задачи линейного программирования.

Множество допустимых решений – это пересечение всех прямых, соответствующих линейным ограничениям типа рав-ва и всех полуплоскостей, соответствующих ограничениям типа нерав-ва.

Для линейной функции градиент – это в-р, состоящий из коэффициентов этой ф-ии. Он показывает направление увеличения ф-ии. Через выбранное решение проводим линию уровня целевой ф-ии. Для линейной ф-ии линия уровня – это прямая, перпендикулярная градиенту.

Геом.интерпретация: область допустимых решений – многогранник в пространстве или многоугольник на плоскости, линии постоянных значений целевой функции. Процесс решения состоит в совмещении линии до конца пересечения с областью допустимых значений при наибольшем значении целевой функции в этой точке пересечения- оптимальное решение ( крайнее положение). Метод-перебор угловых точек.

17. Многошаговые процессы решений в экономике. Суть метода динамического программирования. Параметр состояния и функция состояния системы, рекуррентные соотношения.

Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге. Динамическое программирование — это планирование дальновидное, с учетом перспективы

Некоторые операции естественно распадаются на этапы, в других это деление приходится вводить искусственно. Примером «естественно многоэтапной» операции может служить планирование работы предприятия на некоторый период времени, состоящий из нескольких хозяйственных лет или кварталов.

Динамическое программирование — это вычислительный метод для решения задач управления определенной структуры, когда задача с переменными представляется как многошаговый процесс принятия решений и на каждом шаге определяется экстремум функции только от одной переменной. n

Знакомство с методом динамического программирования

Процесс динамического программирования разворачивается от конца к началу. Сначала делаются различные предположения о том, чем кончился предпоследний шаг, и для каждого из них выбирается управление на последнем. Затем делаются различные предположения о том, чем кончился предпредпоследний шаг, т. е. рассматриваются различные состояния системы на третьем от конца шаге и выбирается управление на втором от концы шаге так, чтобы оно вместе в уже выбранным управлением на последнем шаге обеспечивало наилучший эффект на двух последних шагах, и так далее, вплоть до первого от начала шага, с которого начинался процесс.

Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности.

Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.

Дата добавления: 2018-06-01; просмотров: 426; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!