Непрерывные случайные величины
Непрерывной называется случайная величина Х, если ее функция распределения непрерывна на множестве ее возможных значений.
Распределение непрерывной случайной величины однозначно определяется ее функцией распределения F(x), т.к.:
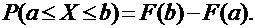
|
Из этой формулы следует, что вероятность каждого конкретного значения непрерывной случайной величины равна нулю.
Все свойства, сформулированные нами в предыдущем подразделе для функций распределения дискретных случайных величин, выполняются и для функций распределения непрерывных случайных величин.
Непрерывную случайную величину можно также задать, используя функцию, которую принято называть плотностью распределения вероятностей, или просто плотностью распределения.
Плотностью распределения непрерывной случайной величины Х называется производная от функции распределения этой случайной величины, т.е.: 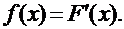
Плотность распределения однозначно определяет распределение непрерывной случайной величины, поскольку:
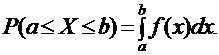
|
И, кроме того, по определению: 
Перечислим основные свойства плотности распределения:
1. Плотность распределения является неотрицательной функцией, т.е. 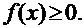
2. 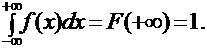
Математическое ожидание М(Х) непрерывной случайной величины Х определяется формулой:

|
Дисперсия D(X) непрерывной случайной величины Х определяется формулой:
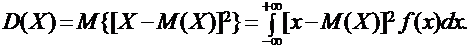
|
На практике для вычисления дисперсии непрерывных случайных величин используется другая формула:
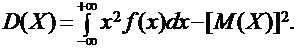
|
Среднее квадратическое отклонение непрерывной случайной величины Х определяется, так же как и для дискретных случайных величин, формулой: 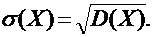
Все свойства математического ожидания и дисперсии, сформулированные нами для дискретных случайных величин, без каких либо изменений остаются справедливыми и для непрерывных случайных величин.
ПРИМЕР:Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х, если она задана функцией распределения вида:
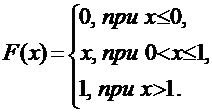
Для данной случайной величины функция распределения является кусочно-непрерывной, поэтому для плотности распределения можно найти:
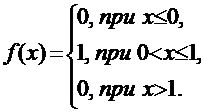
Искомое математическое ожидание случайной величины Х найдем по формуле:
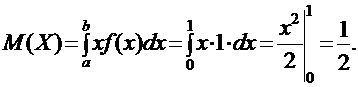
Искомую дисперсию найдем по формуле:
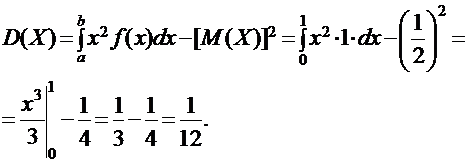
Наконец, среднее квадратическое отклонение найдем по формуле:
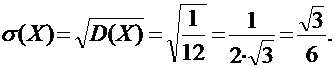
Рекомендуемая литература по теме 1.3:[1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 1.3:
1. Вероятность какого события является значением функции распределения случайной величины?
2. Каким является множество значений дискретной случайной величины?
3. Почему нельзя дискретную случайную величину задавать с помощью плотности распределения?
4. Какая числовая характеристика имеет смысл среднего значения случайной величины?
____________________________________________________________
5. Какая числовая характеристика оценивает степень рассеивания случайной величины?
6. Чем определяется величина скачка функции распределения дискретной случайной величины в точке разрыва?
7. Чему равны наименьшее и наибольшее значения функции распределения?
Тема 1.4. Законы распределения случайных величин
1.4.1. Биномиальное распределение
Пусть проводятся n испытаний по схеме Бернулли с вероятностью успеха р и вероятностью неуспеха q и p + q = 1. В этом случае дискретная случайная величина Х – число успехов может принимать любое из своих возможных значений 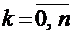 с вероятностями, определяемыми по формуле Бернулли:
с вероятностями, определяемыми по формуле Бернулли:
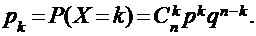
|
Такое распределение называется биномиальным с параметрами р и q.
Заметим, что сумма этих вероятностей будет равна:
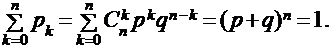
Математическое ожидание и дисперсия случайной величины Х, имеющей биномиальное распределение будет определяться формулами:
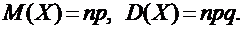
|
ПРИМЕР: Случайная величина Х – число выпадений герба при двух бросаниях монеты имеет биномиальное распределение с возможными значениями 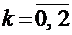 и с вероятностями этих значений, рассчитываемыми по формуле Бернулли соответственно равными: р0 = 0,25, р1 = 0,5 и р2 = 0,25. При этом:
и с вероятностями этих значений, рассчитываемыми по формуле Бернулли соответственно равными: р0 = 0,25, р1 = 0,5 и р2 = 0,25. При этом:
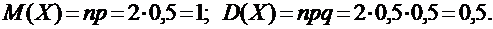
1.4.2. Геометрическое распределение
Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения k = 1, 2, 3, … (счетное множество значений) с вероятностями, определяемыми формулой:
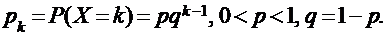
|
Определение является корректным, поскольку сумма вероятностей возможных значений будет равна:
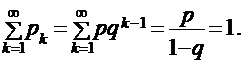
Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний по схеме Бернулли до первого успеха. Математическое ожидание и дисперсия такой величины определяются формулами:
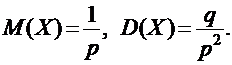
|
ПРИМЕР: В большой партии изделий вероятность брака равна р. Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружилось, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить вероятность р.
Пусть Х – число испытаний до первого появления бракованного изделия. Эта случайная величина имеет геометрическое распределение. Согласно условию ее среднее значение равно: 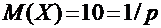 , поэтому р = 1 / 10.
, поэтому р = 1 / 10.
Распределение Пуассона
Дискретная случайная величина Х имеет распределение Пуассона, если она принимает целые значения k = 0, 1, 2, … с вероятностями, определяемыми по формуле Пуассона:
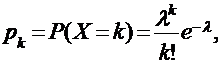
|
где l > 0 – параметр распределения. При этом:

Математическое ожидание и дисперсия величины Х в этом случае:
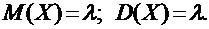
|
Равномерное распределение
Непрерывная случайная величина Х распределена равномерно на отрезке [a, b], если ее плотность распределения имеет вид:
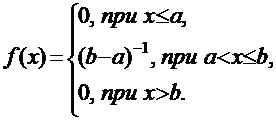
|
График функции плотности распределения в этом случае приведен на рис. 1.2.
Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются формулами:
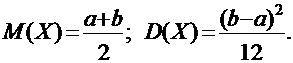
|
ПРИМЕР: Интервал движения автобуса равен 15 минутам. Какова вероятность того, что пассажир на остановке будет ждать автобус более 5 минут?
Пусть случайная величина Х – время ожидания автобуса. Она распределена равномерно на отрезке [0, 15], а ее плотность распределения имеет вид:
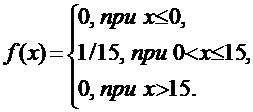
Тогда искомая вероятность будет равна:
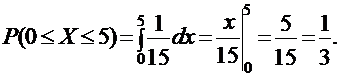
Дата добавления: 2018-06-01; просмотров: 681; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
