Результаты машинных вычислений
Министерство образования и науки, молодежи и спорта Украины
Севастопольский национальный технический университет
Кафедра технической кибернетики
ОТЧЕТ
по лабораторной работе №1:
Решение систем линейных алгебраических уравнений
Выполнил: ст. гр. А-22ДНедуруев С.В.
Проверил: ст. пр.Захаров В. В.
Севастополь
2011
Цель работы
Изучение и освоение прямыхчисленных методов линейной алгебры для решения систем линейных алгебраических уравнений.
Приобретение навыков разработки и применения подпрограмм, реализующих алгоритмы решения систем линейных алгебраических уравнений, вычисления определителей матриц на основе прямых методов.
Изучение и освоение способов реализации соответствующих вычислительных алгоритмов для уменьшения вычислительной погрешности.
2. КРАТКИЕ ТЕОРИТИЧЕСКИЕ СВЕДЕНИЯ
В лабораторной работе необходимо составить, отладить и применить для решения систем линейных алгебраических уравнений, определённых вариантом индивидуального задания, программу решения СЛАУ на основе прямого метода:
Пусть СЛАУ представлена в виде: Ах=b(1)
ГдеА – матрица коэффициентов общего вида, Bвектор правых частей, х -вектор неизвестных;
ПустьА=LU, тогда
LUx=b, Ux = y, откуда следует что метод на основе LU разложения подразумевает решение 2 СЛАУ(1)
|
|
|
Ly = b и Ux=y (2)
Одним из наиболее лучших алгоритмов LU разложения является метод Гаусса. Алгоритм представляетсобойпоследовательностьэтапов, на каждомэтапепроисходитмодификацияматрицы А. Последняямодификация, полученная на (n-1) этапе является искомой матрицей U.
На 1 этапе матрица А приводиться к виду
Для этого 1 строка матрицы А, последовательно умножается на множители:
Li,1=ai1/а11 (3)
И каждый раз вычитается из соответствующей i-й строки матрицы А, заменяя её на полученную в результате вычитания.
На к-м этапе 1-я строка матрицы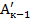 
(k-я строка матрицы Аk-1начиная с k-го элемента) последовательно умножается на множители :
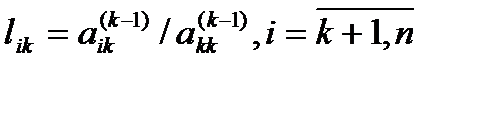(4)
Каждый раз вычитаясь из соответствующей строки матрицы Аk-1 , заменяя её после этого на полученную в результате вычитания, при этом элементы не приведённой к треугольному виду части матрицы 
вычисляются по формуле:
(5)
Искомые элементы матрицы L и есть множители метода LU разложения.
2.1Вычисление определителя
Метод LU – разложения позволяет вычислить определитель матрицы. Так как определитель матрицы равен произведению их определителей, а определитель любой треугольной матрицы равен произведению ее диагональных элементов, тоопределитель матрицы А
|
|
|
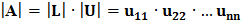(6)
Если при выполнении прямого хода метода LU–разложения, дополнительно реализуется алгоритм полного выбора ведущего элемента., то так как определители матрицы перестановокPrиPcравны единице при четном числе перестановок строкnrncи соответственно минус единице в противном случае, после простых преобразований из первой формулы (6) следует что:
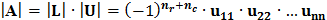(7)
2.2Выбор ведущего элемента
В процессе выполнения k-го этапа LU разложения ведущий элемент 
может оказаться равным 0. Такая ситуация требует перед выполнением очередного этапа выполнения эквивалентных преобразований системы (1), так что бы элемент оказался отличным от 0, если матрица А не вырожденная то такое преобразование всегда возможно. Так как при реализации алгоритма на ПК элемент содержит ошибки вычислений, то модуль элемента обычно сравнивается не с 0,а с некоторым малым положительным числом 
, определяющим погрешность вычислений.
2.3Полный выбор
Перед k-м этапом LU разложения выбирается максимальный по модулю элемент среди элементов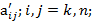 
Затем строка с найденным элементом меняется местами с k-й строкой, столбец с найденным элементом меняется с k-м столбцом местами.
|
|
|
Выполнение LU разложения матрицы А с реализацией стратегии полного выбора, предполагает разложение не матрицы А, а матрицы :
РrAPc =LU
Матрицы перестановок Prи Pcхарактеризуют выполненные перестановки строк и столбцов соответственно. В этом случае описание метода LU разложения принимает следующий вид:
PrAPc=LU
Ly=Pr; Uz=y; x=Pc*z
ВАРИАНТ ЗАДАНИЯ
Необходимо составить отладить и применить программу для решения СЛАУ на основе прямого метода с реализацией стратегии частичного выбора ведущего элемента. При составлении программы необходимо воспользоваться двумя стандартными подпрограммами DECOMPи SOLVE.
Необходимо ввести в подпрограмму DECOMP блок операторов реализующих полный выбор ведущего элемента. Полный выбор предусматривает перестановку не только строк, но и столбцов, поэтому необходимо добавить массив JP,аналогичный массиву IP. Варианты СЛАУ приведены в таблице 1.
Таблица 1 – Варианты СЛАУ
| № варианта | A1x=b1 | A2x=b2 | ||
| A1 | b1 | A2 | b2 | |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 2 3 -2 1 5 2 -0.5 2.1 -3 8 0 -2 0 -0.7 3.4 | 1 -1 0 3.5 | 3 -1 4.5 2 -0.3 1 3 -0.6 1 0 -0.1 3 4 -3 2 1 0 0.1 -3 0 2 -1 0.7 0 4 | 3 1 1 0 -2 |
|
|
|
СХЕМА ПРОГРАММЫ
Основная программа:
Процедура DECOMP:
Процедура SOLVE: Блок 1:
ЛИСТНИНГпрограммы
Program LU;const m=10;Typeivect = array [1..m] of integer;rmatr = array [1..m,1..m] of real;rvect = array [1..m] of real; procedurelmatr(vara,l:rmatr;n:integer);vari,j:integer;Begin for i:=1 to n do for j:=1 to n do begin if i=j then l[i,j]:=1 else if i<j then l[i,j]:=0 else l[i,j]:=a[i,j]; end;end; procedureumatr(varu,a:rmatr;n:integer);vari,j:integer;Begin for i:=1 to n do for j:=1 to n do begin if i>j then u[i,j]:=0 else u[i,j]:=a[i,j]; end;end; procedurewriteall(var a:rmatr;var eps,det:real;n:integer);varl,u:rmatr;i,j:integer;Begin lmatr(a,l,n); umatr(u,a,n); writeln('Matrix L'); for i:=1 to n do Begin for j:=1 to n do write(l[i,j]:7:3); writeln; end; writeln('Matrix U'); for i:=1 to n do Begin for j:=1 to n do write(u[i,j]:7:3); writeln;end;writeln('det(A)=',det:10);writeln;writeln('eps=',eps:10) end; procedure DECOMP(var a:rmatr; varip,jp:ivect;vareps,det:real;varifsolve:boolean;n:integer);label 10;vari,j,k,km,im,jm:integer;s,norm,am:real;Begin ifsolve:=true;det:=1.0; for i:=1 to n do Begin ip[i]:=i; jp[i]:=i; end; norm:=0; for i:=1 to n do Begin s:=0; for j:=1 to n do s:=s+abs(a[i,j]); if norm<s then norm:=s; end; eps:=eps*norm; for k:=1 to n-1 do Begin am:=abs(a[k,k]); for i:=k to n do for j:=k to n do if abs(a[i,j])>am then Begin im:=i; jm:=j; am:=abs(a[i,j]); end; if (im<>k) then Begin for i:=1 to n do Begin am:=a[k,i]; a[k,i]:=a[im,i]; a[im,i]:=am; end; km:=ip[k]; ip[k]:=ip[im]; ip[im]:=km; det:=-det; end; if (jm<>k) then Begin for j:=1 to n do Begin am:=a[j,k]; a[j,k]:=a[j,jm]; a[j,jm]:=am; end; km:=jp[k]; jp[k]:=jp[jm]; jp[jm]:=km; det:=-det; end; if abs(a[k,k])>=eps then for i:=k+1 to n do Begin am:=a[i,k]/a[k,k]; a[i,k]:=am; for j:=k+1 to n do Begin a[i,j]:=a[i,j]-am*a[k,j]; end; end else begin ifsolve:=false; goto 10 end; end; 10: ififsolve and (abs(a[n,n])>=eps ) then for k:=1 to n do begin det:=det*a[k,k]; end elsedet:=0end; procedure SOLVE(var a:rmatr;var ip,jp:ivect;varb,x:rvect;n:integer);vary:rvect;i,j:integer;s:real;Begin for i:=1 to n do Beginy[i]:=b[ip[i]]; end; for i:=2 to n do begin s:=y[i]; for j:=1 to i-1 do begin s:=s-a[i,j]*y[j]; end; y[i]:=s; end; b[n]:=y[n]/a[n,n]; for i:=n-1 downto 1 do Begin s:=y[i]; for j:=i+1 to n do s:=s-a[i,j]*b[j]; b[i]:=s/a[i,i]; end; for i:=1 to n do x[jp[i]]:=b[i];end; procedure unsv(var a1:rmatr;x,b1:rvect;eps:real;n:integer);vari,j:integer;s:real;c:rvect;Begin for i:=1 to n do Begin s:=0; for j:=1 to n do s:=s+a1[i,j]*x[j]; c[i]:=s; end; for i:=1 to n do writeln('x[',i,']=',x[i]:7:3); writeln('Oshibka'); for i:=1 to n do Begin s:=0; s:=abs(c[i])-abs(b1[i]); writeln('delta x[',i,']=',s:10); end;end; Vara,a1:rmatr;b,b1,x:rvect;ip,jp:ivect;f:Text;eps,det:real;i,j,n:integer;ifsolve:boolean;Begin while (n<>5) and (n<>4) do Begin writeln('Vvediterazmer SLAU'); read(n); case n of 4:Assign(f,'Matrix2.txt'); 5:Assign(f,'Matrix.txt'); else writeln('NeverniirazmerSLAU,vvedite 4 ili 5'); end; end; writeln('pogreshost'); read(eps); Reset(f); for i:=1 to n do Begin for j:=1 to n do begin read(f,a[i,j]); a1[i,j]:=a[i,j]; end; read(f,b[i]); b1[i]:=b[i]; end; DECOMP(a,ip,jp,eps,det,ifsolve,n); writeall(a,eps,det,n); if (ifsolve and (abs(det)>eps)) then begin SOLVE(a,ip,jp,b,x,n); unsv(a1,x,b1,eps,n); end elsewriteln('systema ne imeet ed. resheniia'); readln; readln;end.
Результаты ручных вычислений
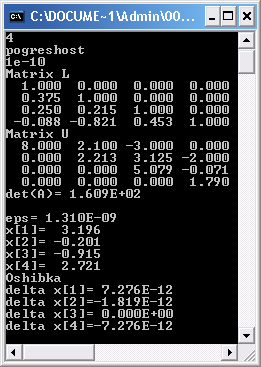
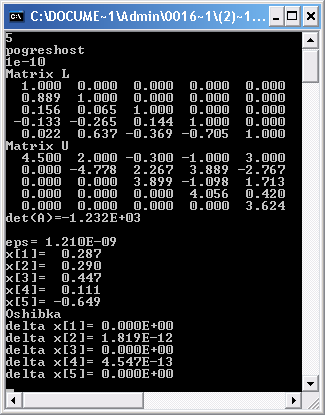
Результаты машинных вычислений
Вывод
В ходе выполнения лабораторной работы изучены и освоены численных методы линейной алгебры: прямые методы решения систем линейных алгебраических уравнений, методы вычисления определителей матриц и обращения матриц.
Приобретены навыки разработки и применения подпрограмм, реализующих алгоритмы решения систем линейных алгебраических уравнений. Так же при помощи разработанной программы были решены две СЛАУ.
Определителиматрицкоэффициентов СЛАУ(1) и СЛАУ(2) далеки от нуля, что свидетельствует о единственности их решения.
Решение СЛАУ(1):x1=3.196; x2 =-0.201;x3=-0.915;x4=2.721;
Решение СЛАУ(2):x1=0.287; x2 =0.290;x3=0.447;x4=0.111;x5=-0.649
Результаты ручных и машинных вычислений совпадают.
Дата добавления: 2018-05-31; просмотров: 145; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!