Интерполяционная формула Лагранжа
ГОУ ВПО КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра систем управления и
технологических комплексов
Дисциплина «Моделирование систем»
Конспект лекций
Краснодар
2009
Тема 4 Идентификация математических моделей статики
технических объектов…………………………………. ………….….…….6
Тема 5 Моделирование и оптимизация в организационно – управ-
ленческих системах цехового уровня ………….6
Тема 6 Моделирование динамики механики приводов
металлообрабатывающих комплексов …………………………………..6
Тема 7 Идентификация математических моделей динамики
технических объектов …………………………………….………………......7
Тема 8 Моделирование линейных одноконтурных САУ……………7
Тема 9 Моделирование линейных многоконтурных САУ……………..8
Тема 10 Моделирование нелинейных многоконтурных САУ …….…8
Введение
При решении задач инжиниринга. проектирования технологии, для их производства не хватает знаний по некоторым вопросам, либо таких знаний нет вовсе.
Моделирование – метод исследования объектов, явлений и процессов, позволяющий получать недостающую информацию, прогнозировать поведение объекта и оптимизировать его конструкцию.
Этапы моделирования:
- уточнение задачи исследования
- анализ известных результатов исследований в данной области
- принятие допущений и упрощений в моделях
|
|
|
- решение вопроса о проведении эксперимента и его подготовки
- проведение экспериментов и обработка результатов с целью получения математических моделей
- составление моделей процессов, явлений, объектов и работы с ней
- формулирование выводов, рекомендаций, положений по поставленной задаче
3 Глобальные идеи автоматизации машиностроения.
По В.Л. Сосонкину повышение экономической эффективности производства на машиностроительных производствах возможно при одновременном осуществления трех идей:
1. Создание развитой станочной периферии.
2. Концепция гибкого производства.
3. Концепция безлюдного производства.
Проблемы станочной периферии.
1. Роботы и погрузчики. Их назначение загрузка и разгрузка метало обрабатывающего оборудования.
2. Транспортные и подающие устройства.
3. Устройство управления точностью.
4. Устройства управления инструментом: настройка, диагностика и замена.
5. Устройство обнаружения бракованных заготовок и изделий.
6. Зажимные и удерживающие устройства.
7. Контролирующее устройство и устройство анализа результатов контроля.
8. Устройство управления процессом резания.
9. Устройство идентификации заготовок и вызова управляющих программ.
|
|
|
10. устройство управления стружкообразованием и уборки стружки.
Концепция гибкого производства.
Т·К → min
Т- время оборачиваемости капитала
К- капитал
К=Кобр+ε·Косн.фонды
Кобр – зарплата, сырье, налоги.
ε – нормативный коэффициент.
В гибких автоматизированных производственных производств есть 3 принципа менеджмента:
1. Недолжно быть бумажной информации.
2. Деталь не должна пролеживать на складе.
3. Цикл производства детали не более 24 часа.
Тема 1 Виды моделирования. Физическое моделирование
Основные сведения о моделировании технических объектов.
Виды моделирования.
Объект – (прототип) проектируемое техническое устройство, сооружение.
Модель – (аналог) уменьшенный, упрощенный образ этого технического объекта, сооружения.
Виды:
- Физическое моделирование - моделирование объектов, процессов и явлений той же физической природы, но с уменьшением линейных размеров.
- Аналоговое моделирование – модели другой физической природы, но имеющие аналогичное математическое описание.
- Математическое моделирование – модели символьные, т.е. явление заменяется символами (уравнениями).
Физическое моделирование.
|
|
|
Основой является подобие объекта исследований и модели.
Теория подобия базируется на теории размерностей.
При исследовании процессов в объекте и модели эти процессы должны быть подобны.
При исследовании течении газа по трубопроводам процессы должны быть подобны гидродинамически.
Гидродинамическое подобие.
Два гидродинамических процесса являются подобными, если обладают одинаковыми значениями критерий Рейнольца:
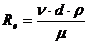
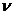 - скорость движения в трубе жидкости
- скорость движения в трубе жидкости
d – характерный диаметр
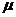 - динамическая вязкость
- динамическая вязкость
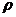 - плотность среды.
- плотность среды.
Основное выражение связывающее перепады давления на трубе с расходом имеет вид:
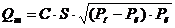
Pн - начальное давление
Pк – конечное давление
C – коэффициент расхода
S – площадь сечения трубы
Режимы (давления) течения жидкости:
1. Ламинарный режим 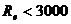

2. Турбулентный режим 3000 < 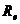 < 10000
< 10000

3. Развитый турбулентный или автомодельный турбулентный режим течения при автомодельном коэффициенте расхода, не зависящем от критерий Рейнольца.
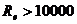
Тепловое подобие.
Баланс тепловой энергии:
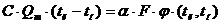
F – поверхность теплообмена
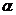 - коэффициент теплообмена. Какая мощность может передаваться поверхностью при перепаде t в 10
- коэффициент теплообмена. Какая мощность может передаваться поверхностью при перепаде t в 10
|
|
|
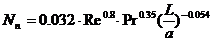
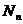 - критерий Нуссельта
- критерий Нуссельта
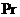 - критерий Прандтля
- критерий Прандтля
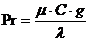
g – ускорение свободного падения
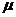 - динамическая вязкость
- динамическая вязкость
С – теплоемкость при постоянном давлении
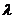 - коэффициент теплопроводности жидкости.
- коэффициент теплопроводности жидкости.
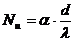
Критериальное уравнение было получено в результате обработке экспериментальных данных. В теории резания к сожалению слабо пользуются теорией подобия.
Ньютоновский пр-с теплообмена:

 - тепловая мощность
- тепловая мощность
 - усредненная температура теплоносителя
- усредненная температура теплоносителя
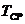 - усредненная температура обрабатываемой среды
- усредненная температура обрабатываемой среды
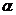 - из критерия Нуссельта.
- из критерия Нуссельта.
Подобие механических систем.
Объект моделирования и модель являются геометрически подобными если между всеми соответствующими их размерами выдерживается один и тот же коэффициент пропорциональности, который называется масштабным коэффициентом размера.
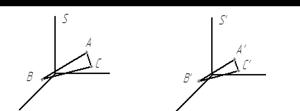
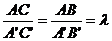
λ – масштабный коэффициент размера.
Соответствующие углы равны.
Площади соотносятся с коэффициентом λ2
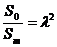
Объем соотносятся с коэффициентом λ3

Кинематическое подобие.
Объект моделирования и модель называются кинематически подобными, если скорости перемещения их точек параллельны и соотносятся с постоянной величиной.
Скорость – перемещение в единицу времени.
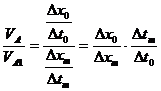
Если объект и модель геометрически подобны если 
Если 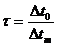 , то
, то 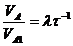 и
и
для ускорений соответствующих точек имеет место соотношение 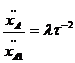
Материальное подобие.
Материальное подобие: две системы называются материально подобными, если массы соответствующих их частей соотносятся с одинаковыми коэффициентами.
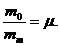
Теорема Ньютона.
Объект моделирования и модель являются механически подобными если они геометрически, кинетически и материально подобны.
Если материал один и то же, то μ=λ3
Тема 2 Аналоговое моделирование
Пример: аналоговое моделирование нагрева электродвигателя.
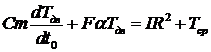
Где 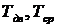 - температуры электродвигателя и окружающей среды;
- температуры электродвигателя и окружающей среды; 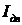 - ток, протекающий по обмоткам электродвигателя;
- ток, протекающий по обмоткам электродвигателя;  - сопротивление обмоток;
- сопротивление обмоток; 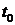 - время в объекте (протипе);
- время в объекте (протипе); 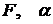 - поверхность теплообмена и коэффициент теплообмена;
- поверхность теплообмена и коэффициент теплообмена; 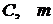 - средняя теплоемкость электродвигателя и его масса.
- средняя теплоемкость электродвигателя и его масса.

Рисунок 1 Схема модели – аналога процесса нагрева электродвигателя.
Уравнение, связывающее Uвх и Uвых. имеет вид

где  - время в модели-аналоге.
- время в модели-аналоге.
Соответствие между переменными объекта и модели- аналога  ,
, 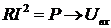 ,
,  при
при  дает следующие масштабные коэффициенты
дает следующие масштабные коэффициенты
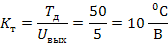 ,
,  ,
, 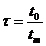
Выразим в диффуравнение нагрева электродвигателя соответствующие переменные в диффуравнение нагрева электродвигателя через переменные модели- аналога
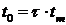 ,
,  ,
, 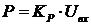
и подставим эти переменные в исходное диффуравнение
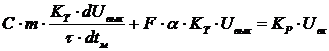
Коэффициенты при соответствующих членах должны быть равны
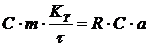
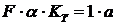
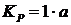
Подобрав подходящее значение множителя 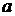 и приняв значения масштабных коэффициентов получим параметры модели-аналога.
и приняв значения масштабных коэффициентов получим параметры модели-аналога.
Модели-аналоги как правило имеют электрическую природу вследствие простоты изготовления и простоты измерения электрических величин.
Тема 3 Задачи восстановления зависимостей
Получение математической модели в статике в зависимости от содержания задачи может быть поставлено двояко:
1. Если математическая модель должна быть точно равна экспериментальным результатам, то ставится задача восстановления зависимости.
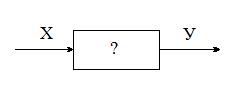

Рисунок 1 – Задача восстановления зависимости функции
Линия, вычисленная по математической модели, должна пройти через все экспериментально заданные точки (рис. 1).
2 Задача сглаживания ставится тогда, математическая модель не может быть точно равна всем экспериментально полученным точкам.
Тогда линия, вычисленная по математической модели, должна проходить наилучшим образом вблизи точек (рис. 2)
.

Рисунок 2 – Задача сглаживания функции
§1 Задача восстановления зависимости
Рассмотрим задачу восстановления зависимости на примере исследования износа режущего инструмента по задней поверхности.
|

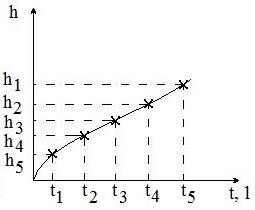
Рисунок 3 –Экспериментально полученные точки износа инструмента
Интерполяционная формула Лагранжа
Самым простым решением такой задачи является использование интерполяционной формулы Лагранжа:
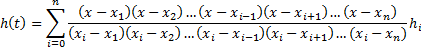 (1)
(1)
Количество слагаемых в ней равно количеству экспериментальных точек (рис. 3). Проверим, проходит ли линия, соответствующая данной функции, точно через все экспериментальные точки, например через точку 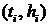 . Примем
. Примем  , тогда все остальные слагаемые, кроме i-ого, равны нулю, а дробь в i-ом слагаемом равна 1, откуда
, тогда все остальные слагаемые, кроме i-ого, равны нулю, а дробь в i-ом слагаемом равна 1, откуда  . Таким образом математическая модель соответствует всем точкам, как показано на рисунке 4..
. Таким образом математическая модель соответствует всем точкам, как показано на рисунке 4..
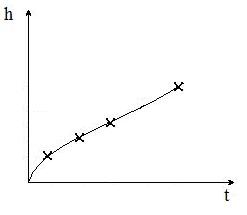
Рисунок 4 – Экспериментальные точки после подстановки
Интерполяционная формула Лагранжа становится громоздкой при большом числе экспериментальных точек и, кроме того, при резких перегибах дает физически недопустимые траектории (уменьшение износа инструмента).
Сплайн – аппроксимация
В настоящее время для восстановления зависимостей чаще используют сплайн – аппроксимацию.
Сплайн это полином 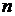 - ой степени, который восстанавливает функцию между двумя соседними точками, которые называют опорными. Ограничимся третьей степенью, что зачастую для технических приложений достаточно. Обычный полином третьей степени
- ой степени, который восстанавливает функцию между двумя соседними точками, которые называют опорными. Ограничимся третьей степенью, что зачастую для технических приложений достаточно. Обычный полином третьей степени
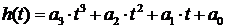 (2)
(2)
имеет четыре коэффициента, которые необходимо определить.
Кубический сплайн представляет собой специфический полином, восстанавливающий функцию между точками 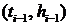 и
и 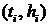 :
:
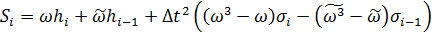 , (5)
, (5)
где
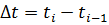 (6)
(6)
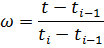 (7)
(7)
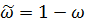 (8)
(8)
в котором имеется лишь один коэффициент 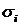 .
.
При аппроксимации кубическими сплайнами восстанавливаемая функция должна быть дважды дифференцируема на всем интервале. Как видно из (5) и (7) в сплайне используется нормированная переменная 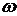 , которая на левой границе равна 0, а на правой –1.
, которая на левой границе равна 0, а на правой –1.
Проверим непрерывность функции, апроксимированная сплайнами. Для этого надо проверить условие
 (9)
(9)
Действительно при 
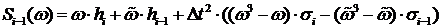 (10)
(10)
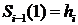
при 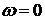
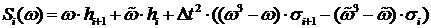 (11)
(11)

Таким образом функция, восстановленная сплайнами, непрерывна при любых коэффициентах сплайна.
Проверим дифференцируемость в i-ой узловой точке
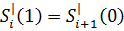 (12)
(12)
Определяем S|i
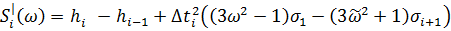 (13)
(13)
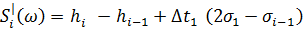 (14)
(14)
 (15)
(15)
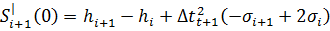 (16)
(16)
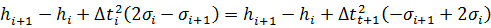 (17)
(17)
Условие дифференциальной функции, восстановленной сплайном, в каждой точке дает линейное дает линейное алгебраическое уравнение относительно неизвестных коэффициентов сплайна.
Проверим
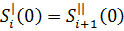 (18)
(18)
 (19)
(19)
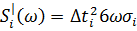 (20)
(20)
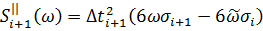 (21)
(21)
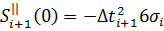 (22)
(22)
При одинаковом шаге экспериментальных данных функция, восстанавливаемая сплайнами, дважды дифференцируема при любых коэффициентах сплайна.
Пусть мы имеем h экспериментальных точек, которые в сплайн аппроксимации называются узловыми точками.
Эти узловые точки разбивают на n-1 участков, поэтому восстанавливаемая функция апроксимируется n-1 сплайнами, которые имеют n-1 неизвестных коэффициентов. Внутренних узловых точек в данной задаче n-2, поэтому количеству уравнений соответствует количество дифференцируемых функций во всех дифференцируемых точках и равно n-2. Таким образом мы имеем систему из n-2 уравнений с n-1 неизвестных.
Для устранения указанной коррекции задачи производят определение задачи в любой конечной узловой точке исходя из графических изображений следующим образом: принимают, что восстанавливаемая функция – функция крайней левой или крайней правой узловой точки – линейная.
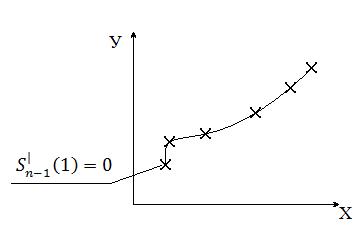
Рисунок 5 – Сплайн-апроксимация
Второй вариант кубического сплайна:

(23)
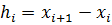 (24)
(24)
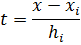 (25)
(25)
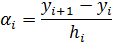 (26)
(26)
где хi и hi – неизвестные коэффициенты сплайна.
Рассмотрим непрерывность сплайна в i-ой точке:

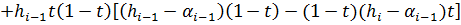 (27)
(27)
Определим непрерывность восстанавливаемой функции в i-ой точке. i-я точка является узловой точкой между сплайнами.
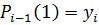 (28)
(28)
 (29)
(29)
Тема 4 Идентификация математических моделей статики технических объектов
Экспертный опрос.
Можно определить существенность факторов, влияющих на выходную величину. Для экспертного опроса формулируют задачу: Расставить факторы Xi, влияющие на величину Y в порядке важности.
Метод ранговых оценок.
| Факторы | X1 | X2i | X3 | … | Xk |
| Ранги | R2k |
Присваивают каждому фактору ранг, в соответствии с его важностью: чем менее важный фактор, тем значение по числу фактора больше (1,2,3,4) r2k второму фактору к эксперту.
Делают сводную таблицу экспертов.
| № эксперта | X1 | X2 | X3 | Xk | |
| 1 | |||||
| 2 | R22 | ||||
| 3 | |||||
| m | |||||
| Сумма рангов | S1 | S2 | S3 | Sk |
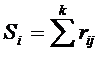

 X3 X1 X4 X2 X5
X3 X1 X4 X2 X5
Сам 2
Важ место
1.Объективны ли результаты экспертов.
2.как это делается.
Метод парных сравнений.
| X1 | X2 | X3 | X4 | |
| X1 | - | 1 | 1 | 1 |
| X2 | 0 | - | 0 | 1 |
| X3 | 0 | 1 | - | 0 |
| X4 | 0 | 0 | - |
Если фактор, стоящий в строке эксперта считается более важный, чем фактор, стоящий в столбце, то на пересечении строки и столбца пишется 1. Если фактор менее важен (строка/столбец), то на пересечении строки и столбца пишется 0.
После этого делают сводную таблицу экспертов, берут таблицы и начинают складывать 1.
| X1 | X2 | X3 | X4 | Ei | |
| X1 | - | 14 | 10 | 7 | 31 |
| X2 | 6 | - | 5 | 4 | 15 |
| X3 | - | ||||
| X4 | - |
После этого суммируют Ei. Чем больше значение суммы, тем более важен фактор.
Тема 6. Моделирование динамики механики приводов
металлообрабатывающих комплексов
Основные понятия о модальных параметрах механики привода


Рис1 рис2
Ск-круговая жесткость вала m-масса тела
J-момент инерции F-приложенная сила
Θ-приложенная сила Сx-жесткость пружины
М-момент
Принцип Даламбера:
М=Ск*Θ + 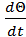 +J
+J 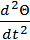 Θ=T(s)
Θ=T(s)
F=Cx+вп 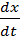 +M
+M 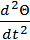
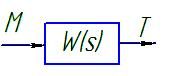 получим передаточную ≈функцию этой системы.
получим передаточную ≈функцию этой системы.
М(s)=Cx×T(s)+BkS×T(s)+J 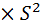 ×T(s)
×T(s)
W(s)= 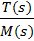 =
= 
Каноничкская передаточная функция колебательного звена (из ТАУ).
Wk(s)= 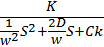
где 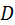 -козффициент демпфирования,
-козффициент демпфирования, 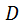 <1
<1
W-собственная частота
К-Коэф. Усиления
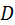 -для стали ≈0,01……0,04
-для стали ≈0,01……0,04
В данной передаточной функции используются следующие модальные параметры:
а) W б) 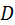 в) К
в) К
Связь между модальными и конструкционными параметрами:
Wk(s)= 
К=  =ек-кручение (податливость участка вала)
=ек-кручение (податливость участка вала)
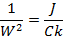
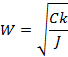
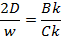
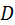 =
= 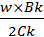 =
=  ×
× 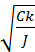 ×
× 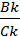 =
= 
АЧХ колебательного звена
АЧХ= 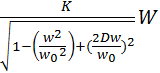
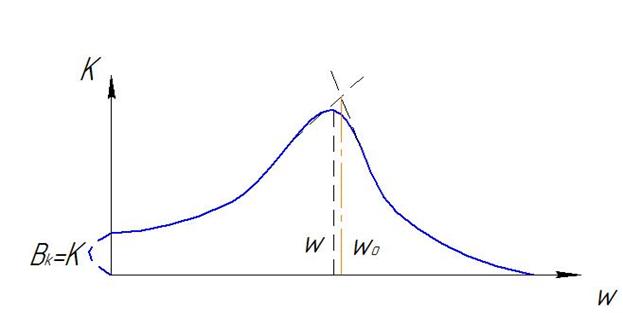
Рис3
При D=0 имеет максимальное значение при W=Wo
 Пусть J=0.1
Пусть J=0.1
C=106 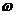 =3160p/c
=3160p/c
B(6=0.2)=20
| B | 15 | 20 | 25 | 100 |
| ω0 | 3150 | 3150 | 3155 | 3080 |
| A(ω0) | 2.11x10-5 | 1.58x10-5 | 1.27x10-5 | 0.167x10-5 |
Собственные частоты в механических системах не зависят от коэффициента внутреннего трения.
Уравнение движения механики привода.
Если мы имеем расчетную схему:
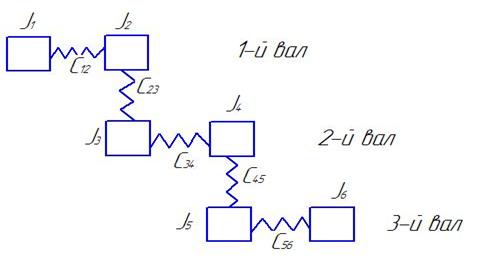
Рис4
Можно эту расчетную схему представить так:

Рис5
Уравнение Лагранжа второго рода:

L – функция Лагранжа;
 – угол поворота движения i-ой массы
– угол поворота движения i-ой массы
 - угловая скорость движения i-ой массы
- угловая скорость движения i-ой массы
(Mgbi – Mci) - момент сопротивления (обобщенный момент)
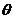 – функция Релея: мощность рассеиваемую диссипативными силами
– функция Релея: мощность рассеиваемую диссипативными силами

n – количество узловых точек
Функция Релея:

Уравнение движения i-той массы
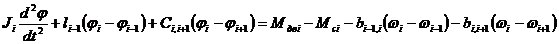
 возникла система из n-дифференциальных уравнений 2-го порядка, где n - количество узловых точек расчетной схемы.
возникла система из n-дифференциальных уравнений 2-го порядка, где n - количество узловых точек расчетной схемы.



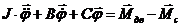
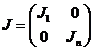
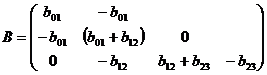
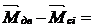 вынуждающие силы
вынуждающие силы
Возьмем 2-х массовую систему
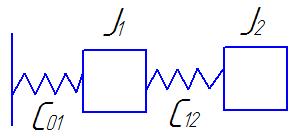
Рис6
1) 
2) 
В механических системах силы демпфирования мало сказываются на собственных частотах
Определения собственных частот
При свободном движении уравнения 1) и 2) имеют вид
1) 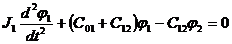
2) 
Примем, что свободное движение имеет такой вид:

Подставим и примем С01=0
При подстановке на sinωt можно сократить

Определитель этой системы относительно неизвестных А1 и А2
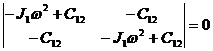
Раскроем этот определитель
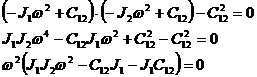
ω0 =1 - 1-ый корень

Определим амплитуды
Подставим в частотное уравнение значения собственных частот, при ω=0
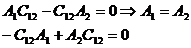
Примем А1=1, тогда А2=1 обозначим вектором 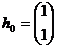



Подставим в частотное уравнение 1-ю собственную частоту. Получим:
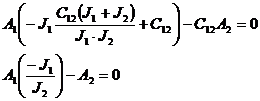
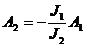 примет А=1
примет А=1
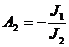
 - векторы безразмерных амплитуд называются собственными формами колебаний.
- векторы безразмерных амплитуд называются собственными формами колебаний.
Собственные формы колебаний не зависят от диссипативных сил в механических системах.
При учете С01 не равном 0 
Количество собственных частот равно количеству сосредоточенных масс или количеству узловых точек. Размерность вектора собственных форм колебаний равна количеству узловых точек.
Свойства собственных форм колебаний
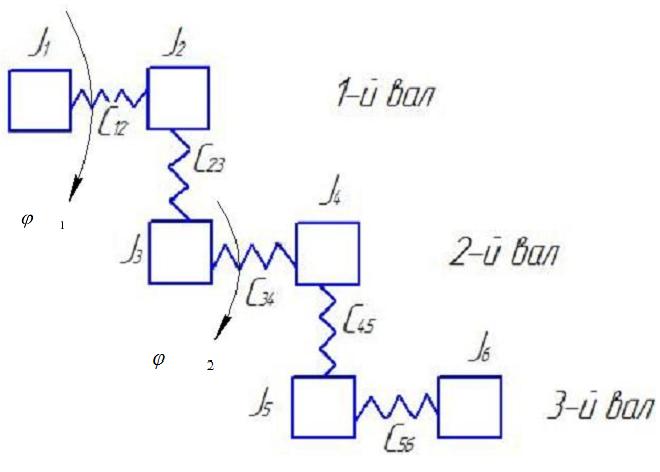
Рис7
Простой цепной расчетной схемой называется схема у которой нет ни одного замкнутого контура.
Свойство собственных форм колебаний:
1) Количество перемен знаков в собственной форме колебаний равно номеру собственной частоты.
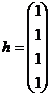
2) Свойство ортогональности – скалярное произведение двух векторов 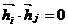 ,
,
если i не равно j.
Разложение передаточных функций по собственным формам колебаний
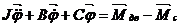
Введем в рассмотрение новую переменную 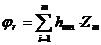
Подставим новые переменные в выражения векторов 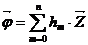

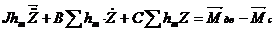
Zm – главные координаты сил.
Умножим


Если механика привода выполнена из материала обладающим одинаковым коэффициентом рассеивания энергии то матрица В
Будет пропорцией матрице С
 если
если 
 (1)
(1)
 ;
;  ;
; 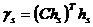

Пусть s=0 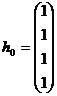
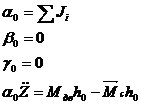
Преобразуем полученные дифференцированные уравнения с помощью прямого интегрального преобразования Лапласа
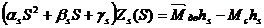
Заменим это выражение обобщенную координату Z на исходные обобщенные координаты
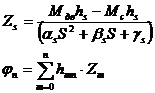
Подставим
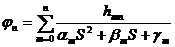

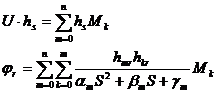
φr – угловая деформация в точке
Mk – момент к точке
Mk =во всех точках 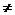 k
k
Передаточная функция 

Дата добавления: 2018-05-31; просмотров: 323; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
