Процедура расчета предельного режима

Без учета самораскачивания

Последовательное утяжеление режима приводит к таким условиям, при которых режим не может существовать. Например, если мощность по электропередаче описывается выражением P = P_max sin d, то увеличение Р возможно только до значения P_max; при задании Р > P_max уравнения установившегося режима не могут быть решены, итерационный процесс решения неизбежно окажется расходящимся. Аналогичная ситуация возникает при снижении напряжения на противоположном от генератора конце электропередачи до U < U_кр: решение уравнений оказывается невозможным. В обоих случаях при некоторых значениях утяжеляемого параметра (Р в первом случае и U во втором) нарушаются условия существования решения, т.е. условия существования установившегося режима.

Понятие о пределе существования режима и о пределе по апериодической устойчивости близки, но не идентичны, так как эти пределы не обязательно совпадают. Например:

1. Решение может существовать, но режим апериодически неустойчив, a_n< 0 (см. ниже).

2. Состояние энергосистемы, граничное по условию существования режимов, может не быть предельным по устойчивости. Это относится к случаям, когда существование режимов лимитируется факторами, непосредственно не связанными с устойчивостью, например, ограничениями реактивной мощности генераторов по условиям нагрева статора и ротора.

При утяжелении режима энергосистемы предельным считается такой режим, в котором нарушается, по крайней мере, одно из следующих условий:

- условия существования режима, т.е. сходимость итерационного процесса расчета;

- дополнительные условия, накладываемые на результаты расчета; это в основном касается уровней напряжения (условие U > U_кр по устойчивости узлов нагрузки), перегрузок линий, трансформаторов и пр.;

- критерии статической устойчивости.

Программа «МАЭСТРО», используемая на кафедре «Передача электрической энергии» НТУ «ХПИ» для расчета установившихся режимов электрических систем, позволяет определять предельные режимы на основании первых двух условий. Далее рассмотрим, каким образом производится проверка статической устойчивости рассчитываемого установившегося режима и возможность объединения процедур самого расчета с этой проверкой на основании третьего условия.

Проверка апериодической устойчивости рассчитанного режима выполняется по знаку свободного члена характеристического уравнения, который может быть вычислен, если определены все параметры этого режима.

Математический анализ показывает, что после снятия малого возмущения изменение любого параметра режима может быть описано выражением вида

Dy(t) = 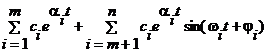, (7.9)

где Dy -отклонение параметра режима от положения равновесия;

t - время;

С_i и j_i некоторые константы.

В этом движении 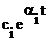есть апериодическая составляющая, а 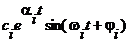- колебательная.

Общий характер движения (7.9) существенно зависит от знаков коэффициентов a. Если значение a отрицательно, то апериодическая составляющая соответствует затухающему экспоненциальному движению, а колебательная – затухающим колебаниям. При a > 0 значение Dy возрастает соответственно апериодически и колебательно.

Характер движения в целом Dy(t) определяется знаками всех коэффициентов a_i: если все a_i меньше нуля, то значение Dy стремится к нулю при t®¥, т.е. режим возвращается к положению равновесия и, следовательно, устойчив. Но если хотя бы одно значение a_i оказывается положительным, то устойчивость нарушается: составляющие движения, у которых a_i < 0, затухнут, а та составляющая, для которой a_i > 0,будет неограниченно возрастать.

Таким образом, осуществить полную проверку статической устойчивости с учетом возможности самораскачивания – это значит определить знаки всех коэффициентов a_i в выражении, описывающем изменение параметра режима после малого возмущения.

Если дифференциальные уравнения, описывающие все элементы исследуемой энергосистемы, известны, то определение вида зависимости Dy(t) представляет собой чисто математическую проблему. В максимально упрощенной форме решение рассматриваемой задачи сводится к ряду этапов, которые иллюстрируются ниже на простейшей схеме, показанной на рис. 7.2.

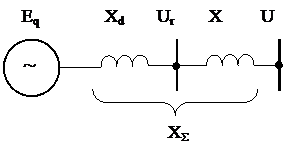Рис.7.2. Схема «генератор - шины бесконечной мощности».

Мощность генератора в этой схеме при неустановившемся режиме, в частности при качаниях, описывается уравнением

Р_г = Р_max sin d + k_д 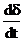, (7.10)

т.е. кроме синхронной мощности генератора, равной Р_maxsind, имеется и асинхронная мощность, соответствующая асинхронному моменту. При малых скольжениях эту мощность можно считать пропорциональной S и представлять в виде Р_ас = k_дS = k_д , где k_д – некоторый коэффициент.

Переходным процессом в схеме (см. рис. 7.2) соответствует система уравнений

; (7.11)

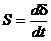; (7.12)

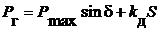; (7.13)

где t_j-механическая постоянная инерции генератора вместе с турбиной мощностью Р_т. Переменными параметрами здесь являются угол d, скольжение S и активная мощность генератора Р_г. В результате кратковременного возмущения эти параметры отклоняются от исходных значений d₀, S₀=0, Р_г=Р_г0, соответствующих состоянию равновесия.

I этап анализа устойчивости: линеаризация уравнений в точке рассматриваемого режима и замена исходных переменных их отклонениями от положения равновесия.

Линеаризация состоит в том, что все нелинейные зависимости между переменными, например, синусоидальная зависимость Р_гот d, заменяются в малой окрестности положения равновесия на линейные, т.е. кривые заменяются касательными к ним. Без линеаризации получение решения дифференциальных уравнений, описывающих электрическую систему, в аналитическом виде невозможно. Для линеаризации уравнений осуществляется замена переменных: вместо каждого параметра режима y вводится y₀+Dy, y₀ - значение этого параметра в заданном (проверяемом на устойчивость) режиме. Полученные таким образом уравнения упрощаются с учетом того, что все Dy малы.

В случае уравнений (7.11) - (7.13) выполняется замена d = d₀+Dd, S = S₀+DS=DS, Р_г= Р_го+DР_г и учитывая, что Dd мало cos Dd ≈ 1, а sin Dd ≈ Dd имеем:

;

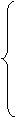
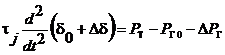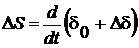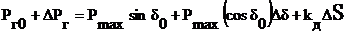Очевидно, что

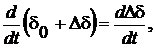
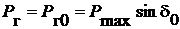поэтому имеем

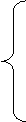
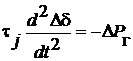; (7.14)

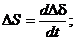(7.15)

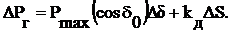(7.16)

II этап: приведение системы линеаризованных уравнений (7.14) – (7.16) к одному уравнению путем исключения всех переменных, кроме одного, любого.

Если исключить, например, переменное DР_ги DS, то получим

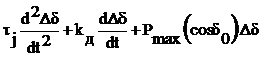=0. (7.17)

Это есть дифференциальное уравнение, описывающее рассматриваемую электрическую систему при малых отклонениях от положения равновесия.

III этап: применение операторного метода решения дифференциальных уравнений.

По этому методу осуществляется переход от дифференциального уравнения, содержащего производные переменной величины по времени, к эквивалентному уравнению в операторной форме. Для уравнений, где переменной служит отклонение Dy от положения равновесия, переход к операторной форме сводится к замене d/dt на р, d²/dt² на р² и т.д., где р – оператор. Полученное уравнение рассматривается как алгебраическое уравнение относительно р.

В нашем примере из (7.17) следует

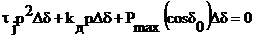
или, поскольку р является алгебраическим множителем,

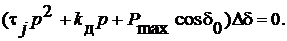
Так как представляет интерес случай, когда Dd ¹ 0, то

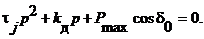(7.18)

Уравнение (7.18) называется характеристическим. Оно не зависит от того, какая из переменных величин использовалась при его получении. При более сложной системе исходных дифференциальных уравнений повышается степень относительно р, т.е. имеем уравнение n-ной степени p:

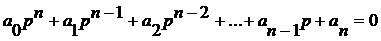(7.19)

или в краткой записи D(р) = 0.

IV этап: решение алгебраического уравнения (7.19) относительно р.

Искомые значения a_i [см. уравнения (7.9)] определяются как действительные части корней р_j (j=1,2,…,n) характеристического уравнения. Число корней равно порядку n характеристического уравнения.

Корни могут быть действительными: р=a, тогда каждому из них соответствует апериодическая составляющая 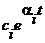, или комплексно-сопряженным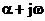и: р= и р= 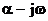, тогда каждой паре таких корней соответствует составляющая вида 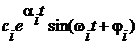. После того как найдены все корни характеристического уравнения и определены знаки a_i, задача проверки статической устойчивости оказывается решенной.

В случае, если энергосистема устойчива (все a_i< 0), говорят о том, что она имеет все «левые» корни. Действительные и комплексно-сопряженные корни, где a_i>0, называют «правыми». Это соответствует отображению корней характеристического уравнения на комплексной плоскости.

Сложность определения необходимых и достаточных условий статической устойчивости и известная из практики малая вероятность колебательного нарушения устойчивости при увеличении перетока по межсистемным связям хорошо объясняют повышенный интерес к приближенным способам оценки статической устойчивости – определению только необходимых ее условий, т.е. проверки устойчивости без учета самораскачивания.

Упрощенная проверка статической устойчивости состоит в следующем. Существует известное свойство корней алгебраического уравнения: если p₁, p₂,…, p_n – корни уравнения

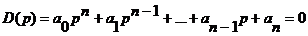, (7.20)

то оно может быть представлено в виде

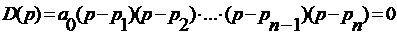. (7.21)

Свободный член характеристического уравнения (7.20), равный a_n, может быть получен подстановкой р=0 в выражение (7.20), т.е. D(0) = a_n. Такая же подстановка в (7.21) дает

D(0) = a₀(-р₁)(-р₂)×…×(-р_n-1)(-р_n),

откуда, сгруппировав корни по признаку наличия или отсутствия мнимой части, получаем

a_n = a₀(-р₁)(-р₂)×…×(-р_m) ´ (-р_m+1) (-р_m+2)×…× (-р_n). (7.22)

¹⁴⁴⁴⁴²⁴⁴⁴⁴³¹⁴⁴⁴⁴⁴⁴²⁴⁴⁴⁴⁴⁴³

^{действительные корни комплексно-сопряженные корни вида}^a^±^j^w

Поскольку в этом выражении комплексные корни представлены только парами сомножителей (р_i = a+jw, р_i₊₁ = a-jw), число таких корней четно и произведение (-р_i) 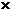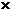(-р_i₊₁) для каждой пары корней положительно:

(-р_i) (-р_i₊₁) = [-(a+jw)] [-(a-jw)] = a²+w² > 0. (7.23)

Поэтому из (7.22) следует, что знак свободного члена характеристического уравнения (sign a_n) определяется знаком произведения a₀(-р₁)(-р₂)×..… (-р_m), т.е.

sign a_n = sign[a₀(-р₁)(-р₂)×…×(-р_m)]. (7.24)

Если энергосистема устойчива, то все действительные корни отрицательны: р₁ < 0, р₂ < 0,…,р_m < 0, а произведение этих корней, взятых с обратными знаками, (-р₁)(-р₂)×.×(-р_m) положительно.

При последовательном изменении параметров режима в сторону приближения к пределу устойчивости (утяжеление режима) знак a₀ не изменяется, поэтому, как следует из (7.24), смена знака a_n по сравнению с исходным заведомо устойчивым режимом означает, что стал положительным один из действительных корней. Следовательно, изменение знака a_n при утяжелении режима определяет границу апериодической устойчивости. К колебательным нарушениям устойчивости знак a_n не чувствителен. Свободный член характеристического уравнения a_n вычисляется для заданного режима энергосистемы по достаточно простому алгоритму.

При чрезмерно больших шагах утяжеления режима возможно одновременное, т.е. в пределах одного шага, изменение знака двух или любого четного числа действительных корней характеристического уравнения, тогда a_n не изменится. Уменьшение шагов утяжеления по мере приближения к пределу устойчивости делает случаи «проскакивания» предела менее вероятными, а несомненные вычислительные преимущества этого критерия способствуют его использованию в алгоритмах и программах расчета статической устойчивости.

Например, для пятиузловой схемы, где узел 5 балансирующий, в узлах 1 и 2 имеются генераторы, а в узлах 3 и 4 – нагрузки, свободный член характеристического уравнения равен значению определителя:

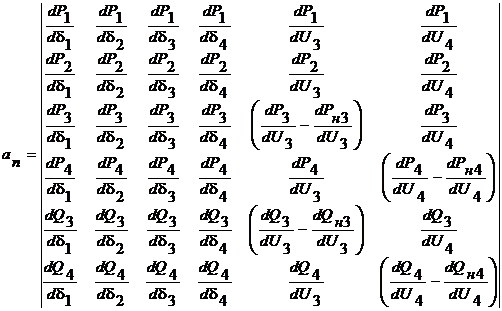(7.25)

где P_i, Q_i – мощности, притекающие в i-й узел из сети;

P_нi(U_i), Q_нi(U_i)-статические характеристики нагрузки в i-м узле.

Необходимость выполнять после расчета установившегося режима проверку его апериодической устойчивости по специальному алгоритму усложняет программу. Поэтому естественно стремление объединить процедуру самого расчета режима с проверкой апериодической устойчивости. Это оказывается возможным при использовании специальным образом организованного итерационного процесса, а также и при применении метода Ньютона для расчета режима.

Так, выражение для свободного члена характеристического уравнения при выполнении ряда условий совпадает с якобианом уравнений установившегося режима, т.е. с определителем, составленным из элементов матрицы Якоби, используемой при решении уравнений по методу Ньютона. Эти условия следующие:

1) в расчетной схеме должен быть узел, рассматриваемый как шины бесконечной мощности, причем этот узел должен быть принят балансирующим;

2) при определении апериодической устойчивости нужно пренебрегать статизмом АРВ, т.е. считать, что АРВ поддерживает напряжение в генераторном узле в точности неизменным;

3) генераторы в расчете режима должны быть заданы значениями Р_г, U_г, но не Р_г, Q_г;

4) в расчете режима и при проверке его апериодической устойчивости должны фигурировать одни и те же статические характеристики нагрузки.

Проверка по знаку якобиана, так же как и проверка по знаку свободного члена характеристического уравнения, требует мелких шагов утяжеления вблизи предела. Полезно также иметь в виду, что сам граничный режим, для которого якобиан решаемой системы уравнений равен нулю, не может быть рассчитан (итерационный процесс не сойдется), но приблизиться к нему с точностью до единиц мегаватт возможно.

Дата добавления: 2018-05-31; просмотров: 320; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 23 24 25 26 272829 30 31 32 Следующая ⇒

Мы поможем в написании ваших работ!