Гармонические функции. Восстановление аналитической функции.
Пусть на области 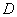 плоскости
плоскости  задана аналитическая функция
задана аналитическая функция 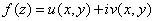 . Тогда, как это уже было отмечено в § 6.2, функция
. Тогда, как это уже было отмечено в § 6.2, функция 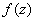 имеет на
имеет на 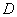 непрерывные производные любого порядка. Но тогда функции
непрерывные производные любого порядка. Но тогда функции 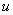 и
и 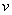 имеют на
имеют на 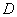 непрерывные частные производные любого порядка, а первые производные удовлетворяют условиям Коши – Римана.
непрерывные частные производные любого порядка, а первые производные удовлетворяют условиям Коши – Римана.
Определение 1. Функция 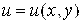 Называется гармонической в области D, если она имеет в этой области непрерывные частные производные до второго порядка включительно и в этой области лапласиан
Называется гармонической в области D, если она имеет в этой области непрерывные частные производные до второго порядка включительно и в этой области лапласиан 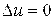
 Определение 2. Две гармонические функции
Определение 2. Две гармонические функции 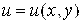 ,
, 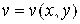 , удовлетворяющие условию (3.2), называются сопряженно - гармоническими функциями. Теорема. Для того, чтобы функции
, удовлетворяющие условию (3.2), называются сопряженно - гармоническими функциями. Теорема. Для того, чтобы функции 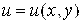 ,
, 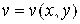 были соответственно действительной и мнимой частями аналитической функции
были соответственно действительной и мнимой частями аналитической функции 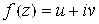 , необходимо и достаточно, чтобы они были сопряженно-гармоническими функциями. Пользуясь условиями Коши-Римана, аналитическую функцию
, необходимо и достаточно, чтобы они были сопряженно-гармоническими функциями. Пользуясь условиями Коши-Римана, аналитическую функцию 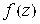 можно восстановить, если известна ее действительная
можно восстановить, если известна ее действительная 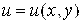 Или мнимая часть
Или мнимая часть  .
.
Геометрический смысл модуля и аргумента производной.
Пусть функция 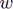 = f(z) аналитична в некоторой области D ⊂
= f(z) аналитична в некоторой области D ⊂ 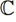 и отображает область D плоскости z в область G плоскости
и отображает область D плоскости z в область G плоскости 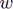 . Представим её производную в произвольно заданной точке z0 ∈ D в показательной форме:
. Представим её производную в произвольно заданной точке z0 ∈ D в показательной форме:
f′(z0) = 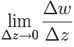 = keiα. = keiα.
| (4.7) |
Тогда отображение, осуществляемое функцией f(z), переводит бесконечно малую окрестность точки z0 ∈ D в подобную окрестность точки 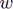 0 = f(z0) ∈ G, поворачивая её на угол α и растягивая в k раз.
0 = f(z0) ∈ G, поворачивая её на угол α и растягивая в k раз.
|
|
|
Убедимся в этом. Из (4.7) следует
Δ 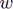 = Δz · k ·eiα +
= Δz · k ·eiα + 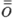 (Δz), при Δz → 0. Рассмотрим главное слагаемое: Δz · keiα. Поскольку при умножении комплексных чисел их модули перемножаются, а аргументы складываются,
(Δz), при Δz → 0. Рассмотрим главное слагаемое: Δz · keiα. Поскольку при умножении комплексных чисел их модули перемножаются, а аргументы складываются,
|Δ 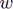 | ≈ k |Δz|, arg |Δ | ≈ k |Δz|, arg |Δ 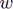 | ≈ arg |Δz| + α. | ≈ arg |Δz| + α.
| (4.8) |
Таким образом, функция f(z) растягивает в k раз окрестность точки z0 и поворачивает её на угол α.
Дробно-линейное отображение. Круговое свойство, ангармоническое отношение, отображение окружности на окружность.
Дробно-линейная функция 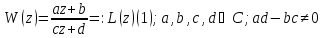 Обратно, z можно выразить через W:
Обратно, z можно выразить через W: 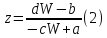 Таким образом, соответсвуют формулы (1) является взаимно однозначным точка
Таким образом, соответсвуют формулы (1) является взаимно однозначным точка 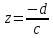 будет соответствоватьW=∞, а точка
будет соответствоватьW=∞, а точка 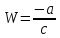 - точкаz=∞. Функция (1) сохраняет углы во всех точках расширенной плоскости
- точкаz=∞. Функция (1) сохраняет углы во всех точках расширенной плоскости 
Теор: Образом прямой или окружности при отображении 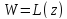 является прямая или окружность.
является прямая или окружность.
Дробно-линейное отображение 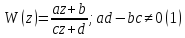 Зависит от трех параметров, за которые могут принять, например, отношение чисел a, b, c, dк одному из них. Эти параметры однозначно определяется из требований, чтобы три заданных точки z1 , z2 , z3 плоскости
Зависит от трех параметров, за которые могут принять, например, отношение чисел a, b, c, dк одному из них. Эти параметры однозначно определяется из требований, чтобы три заданных точки z1 , z2 , z3 плоскости 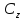 переходит в заданные точкиW1 , W2 , W3 плоскости
переходит в заданные точкиW1 , W2 , W3 плоскости 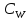 :
: 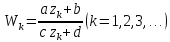 Чтобы исключитьa, b, c, d из этих уравнений и из уравнения
Чтобы исключитьa, b, c, d из этих уравнений и из уравнения 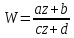 образуем разности:
образуем разности: 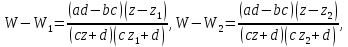
|
|
|
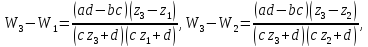 Отсюда получим
Отсюда получим 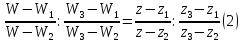 Разрешаем (2) относительно W, получим искомое дробно-линейное отображение. Оно переводит точки z1 ,z2 , z3и окрестность
Разрешаем (2) относительно W, получим искомое дробно-линейное отображение. Оно переводит точки z1 ,z2 , z3и окрестность  соответственно в три точкиW1 , W2 , W3и проходят через них окрестность
соответственно в три точкиW1 , W2 , W3и проходят через них окрестность  Тройки точекz1 , z2 , z3и W1 , W2 , W3 определяют направление обхода на
Тройки точекz1 , z2 , z3и W1 , W2 , W3 определяют направление обхода на 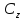 и
и 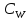 соответственно, причем области остающиеся при этих обходах слева (справа) соответствуют друг-другу при отображении (2). Это является непосредственным следствием конформности дробно-линейного отображения.
соответственно, причем области остающиеся при этих обходах слева (справа) соответствуют друг-другу при отображении (2). Это является непосредственным следствием конформности дробно-линейного отображения.
Отсюда принимаем во внимание, что при отображении (1) в случае действительных a, b, c, d Действительная ось ImZ=0 переходит в действительную ось ImW=0 и при ImZ=0 знак 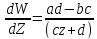 совпадает со знаком ad-bc. Получим следующие утверждения
совпадает со знаком ad-bc. Получим следующие утверждения
Теор1: При невырожденном дробно-линейном отображении (1) с действительными коэффицентами верхняя полуплоскость ImZ>0 переходит в верхнюю полуплоскость ImW>0, если ad-bc>0 и нижнюю, если ad-bc<0
Опр:Выражение 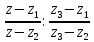 называется двойным. Равенство (2) означает инвариантность ангармонического отношения четырех точек при невырожденном дробно-линейном отображением
называется двойным. Равенство (2) означает инвариантность ангармонического отношения четырех точек при невырожденном дробно-линейном отображением
Теор2: (свойство сохранения симметрии) Если точки z1 ,z2симметричны относительно некоторой прямой или окружности при дробно-линейном отображении 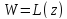 их образы будут симметричны относительно образовγ:
их образы будут симметричны относительно образовγ: 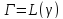
|
|
|
Интегральная теорема Коши.
Теорема. Пусть функция f(z) дифференцируема в односвязной области D и её производная непрерывна в D. Тогда интеграл от f(z) по любой замкнутой кривой γ, лежащей в области D, равен нулю:
∫γf(z)dz=0.
Доказательство.Если f(z)=u(x,y)+iv(x,y), то по формуле
∫γf(z)dz=∫γudx−vdy+i∫γvdx+udy
имеем
∫γf(z)dz=J1+iJ2,
где
J1=∫γudx−vdy, J2=∫γvdx+udy.
Так как функция f(z) имеет непрерывную производную в области D, то частные производные первого порядка функции u,v непрерывны в области D и выполняется условия Коши-Римана
∂u∂x=∂v∂y, ∂v∂x=−∂u∂y
В силу применимости формулы Грина следует, что J1=J2=0. Таким образом
∫γf(z)dz=J1+iJ2=0
Интегральная формула Коши.
Пусть функция f(z) дифференцируема в односвзяной области D и пусть простая замкнутая кривая γлежит в D и ориентирована положительно. Тогда для любой точки z, лежащей внутри γ, справедлива формула
f(z)=12πi∫γf(ζ)ζ−zdζ это формула называется интегральной формулой Коши.
Доказательство. Функция f(ζ)/(ζ−z) дифференцируема в области D с выколотой точкой z. Выберем ρтак, чтобы круг |ζ−z|<ρ вместе с его границей Cρ:|ζ−z|=ρ лежал внутри γ. Тогда используя следствие из интегральной теоремы Коши, получаем
|
|
|
J=12πi∫γf(ζ)ζ−zdζ=12πi∫Cρf(ζ)ζ−zdζ
=12πi∫Cρf(ζ)−f(z)+f(z)ζ−zdζ=J1+f(z)12πi∫Cρdζζ−z
где J1=12πi∫Cρf(ζ)−f(z)ζ−zdζ.
Так как 12πi∫Cρdζζ−z=1, то
J=12πi∫Cρf(ζ)−f(z)ζ−zdζ+f(z)
и поэтому для доказательства достаточно установить, что J1=0.
В силу непррывности функции f(ζ) в точке z для любого ε>0 найдется такое δ=δ(ε)>0, что неравенство |f(ζ)−f(z1)|<ε выполняется при |ζ−z|<δ. Следовательно
|J1|⩽12π∫Cρ|f(ζ)−f(z)||ζ−z||dζ|<12περ∫Cρ|dζ|=ε,
если ρ⩽δ. Учитывая, что J1 не зависит от ρ, получаем J1=0, т.е. J=f(z). Формула доказана.
Дата добавления: 2018-06-27; просмотров: 913; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
