Лабораторная работа № 6. Метод сеток для задачи Дирихле.
Задание:
Применяя метод сеток с шагом h=0,25, найти решение u(x,y) уравнения Лапласа в квадрате с вершинами А(0,0), B(0,1), C(1,1), D(1,0). Краевые условия приведены в таблице 2.2.
Таблица 2.2
Варианты заданий к лабораторной работе № 6
| Номер варианта |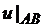 
| 
| 
| 
|
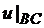
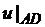
| 1 |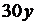 
| 
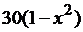
| 0 | 0 |
| 2 |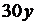
| 
| 
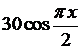
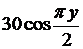
| 0 |
| 3 |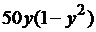 
| 0 | 0 |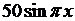 
|
| 4 |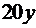 
| 
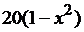
| 0 | 0 |
| 5 |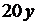 
| 
| 
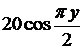
| 0 |
| 6 |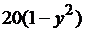 
| 0 | 0 |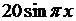 
|
| 7 |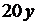
| 20 |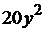 
| 
|
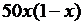
| 8 |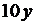 
| 10 |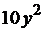 
| 
|
| 9 | 0 |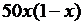
|
|
|
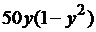
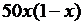
| 10 |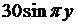 
| 20x | 20y |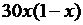 
|
| 11 |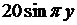 
| 10x | 10y |
|
| 12 |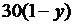 
| 
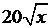
| 20y |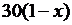 
|
| 13 | 
| 
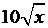
| 10y |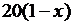 
|
| 14 |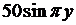 
| 
| 
|
|
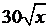
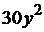
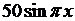
| 15 |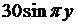
|
|
| 
|
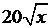
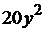
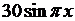
| 16 |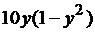 
| 0 | 0 |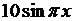 
|
Лабораторная работа № 7. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана)
Задание.
Найти приближенное решение уравнения Лапласа с шагом h=1/8 в квадрате с вершинами А(0,0)), B(0,1), C(1,1), D(1,0), используя процесс усреднения Либмана. Краевые условия приведены в таблице 2.2. Итерации проводить до тех пор, пока разности между последоватеными значениями функций для всех точек не станут меньше 0,01.
Глава 2. Приближенные методы решения интегральных уравнений
Справочный материал по приближенным методам решения интегральных уравнений
Рассмотрим интегральное уравнение Фредгольма второго рода6
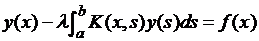(3.1)
Идея метода конечных сумм заключается в замене определенного интеграла конечной суммой с помощью одной из квадратурных формул
|
|
|
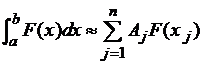(3.2)
где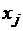 
- абсциссы точек отрезка [a,b], 
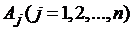- коэффициенты квадратурной формулы, не зависящие от F(x). Заменяя приближенно интеграл в уравнении (3.1) по формуле (3.2) и полагая 
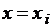, получим систему линейных уравнений относительно значений 
:
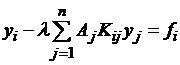(i=1,2,…,n) , (3.3)
где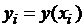 
, 
, 
.
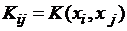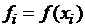Решив эти системы линейных уравнений одним из известных методов (Гаусса, итераций), мы получим таблицу приближенных значений yi в точках xi. В результате получаем решение уравнения (3.1) в виде
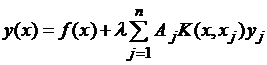(3/4)
В зависимости от выбора квадратурной формулы (3.2), будем иметь следующие значения коэффициентов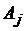 
и абсцисс 
:
1) для формулы трапеций:
, 
, 
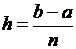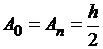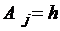(j=1,2,…, n-1). 
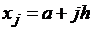(j=0,1,…, n).
2) для формулы Симпсона:
n=2m,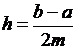 
, 
, 
,
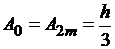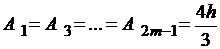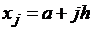, (j=0,1,…,2m).
Пример 3.1: Используя квадратурную формулу Симпсона при n=2, найти приближенное решение интегрального уравнения:
(3.5)
Для формулы Симпсона имеем
, 
, 
, 
, 
, 
.
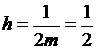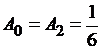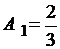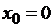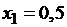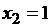Уравнение (3.5) можно переписать:
.
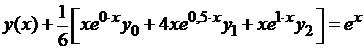Полагая в последнем равенстве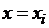 
, получаем систему
|
|
|
.
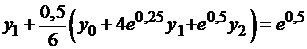
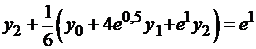После упрощения система принимает вид:
Решив эту систему, получаем: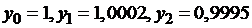 
.
Получаем приближенное решение уравнения:
.
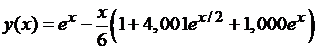Лабораторная работа № 8. Решение уравнения Фредгольма второго рода методом конечных сумм
Задание:
Применяя квадратурную формулу:
a) трапеций (n=2);
б) Симпсона (n=2)
найти приближенное решение интегрального уравнения.
Варианты заданий к лабораторной работе № 8
| № 1. |  .
|
| № 2. |  .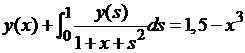
|
| № 3. |  .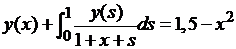
|
| № 4. |  .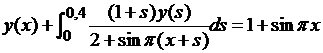
|
| № 5. |  .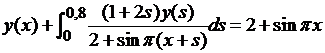
|
| № 6. |  .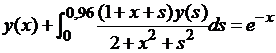
|
| № 7. |  .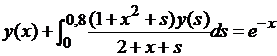
|
| № 8. |  .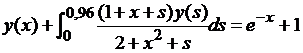
|
| № 9. |  .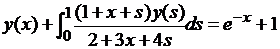
|
| № 10. |  .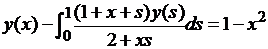
|
| № 11. |  .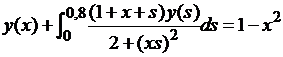
|
| № 12. |  .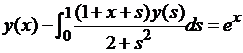
|
| № 13. |  .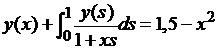
|
| № 14. |  .
|
| № 15. |  .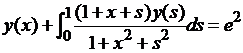
|
| № 16. |  .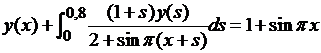
|
Глава 4. Статистическая обработка данных
Справочный материал по статистической обработке данных
Пусть мы имеем массив экспериментальных данных, состоящий из п чисел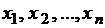 
. Можно считать, что эти числа являются значениями некоторой случайной величины Х.
Множество всех возможных значений рассматриваемой случайной величины называют генеральной совокупностью, а множество опытных данных −выборочной совокупностью.
Цель статистической обработки данных состоит в том, чтобы по характеристикам выборочных совокупностей судить о свойствах генеральных совокупностей.
|
|
|
Величину М, определяемую по формуле:
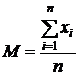(4.1)
называют выборочным средним. Величина М даёт оценку математического ожидания (генеральной средней) случайной величины Х.
Оценку генеральной дисперсии даёт выборочная дисперсия. Она вычисляется по формуле:
или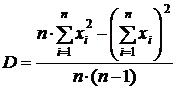 
. (4.2)
Корень квадратный из выборочной дисперсии называют выборочным средним квадратическим отклонением: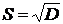 
.
Среднее квадратическое отклонение имеет ту же размерность, что и элементы исходного массива. Это не даёт возможности сравнивать между собой степень рассеяния (изменчивость) разнородных величин. Меру изменчивости, не зависящую от единиц измерения исходных величин, даёт коэффициент вариации С:
.
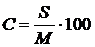Будем предполагать, что в результате опыта мы имеем не только массив данных 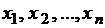, но и связанный с ним массив 
.
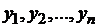Результаты такого опыта можно рассматривать, как набор экспериментальных точек, абсциссами которых являются значения случайной величины Х, а ординатами − соответствующие им значения случайной величины У: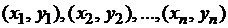 
.
Допустим, что у нас есть основание предполагать, что между переменным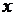и 
и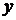 
существует зависимость вида y=f(x).
|
|
|
Выбор типа функции f(x) основывается на теоретических исследованиях и анализе взаимного расположения экспериментальных точек. Предполагаемая зависимость, как правило, не является строго функциональной. Поэтому при любом выборе параметров функции f(x) вычисленные значения f(xi) не совпадают с наблюдаемыми значениями уi, т.е. разность уi - f(xi) отлична от нуля.
Подберём параметры функции f(x) так, чтобы сумма квадратов была минимальна. Геометрически это означает, что мы хотим провести линию с уравнением y=f(x) как можно "ближе" к имеющимся экспериментальным точкам. Предположим, что наша зависимость является линейной:
f(x)=ах + b.
Мы должны подобрать параметры а и b так, чтобы минимизировать выражение:
.
Для определения коэффициентов а и b необходимо решить систему уравнений
.
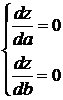После выполнения преобразований система примет вид:
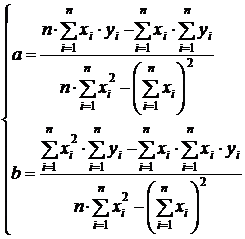
Прямая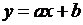 
называется линией регрессии у на х, а коэффициенты а, b − коэффициентамирегрессии.
Показателем, характеризующим тесноту линейной связи между х и у, является (выборочный) коэффициент корреляции r:
.
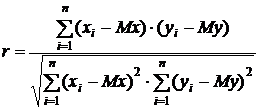Коэффициент корреляции r и коэффициент регрессии а связаны соотношением:
,
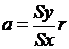где 
– средние квадратические отклонения рассматриваемых значений Х и У соответственно.
Значение коэффициента корреляции удовлетворяет соотношению: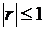 
. Чем меньше отличается 
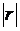от 1, тем ближе к линии регрессии располагается экспериментальные точки.
Если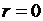 
, то переменные х, у называются некоррелированными. Для того чтобы проверить, значимо ли отличается от нуля выборочный коэффициент корреляции, можно воспользоваться критерием Стьюдента.
Вычисленное значение критерия определяется по формуле:
.
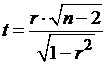Вычисленное значение t сравнивается со значением из таблицы распределения Стьюдента в соответствии с уровнем значимости α и числом степени свободы п - 2. Если вычисленное значение больше табличного, то выборочный коэффициент корреляции значимо отличен от нуля.
Пример 4.1:
Результаты статистических испытаний представлены и таблице 4.1.
Таблица 4.1.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| xi | 1,81 | 2,21 | 2,09 | 1,55 | 1,60 | 1,52 | 1,63 | 1,58 | 1,81 | 2,27 | 0,97 | 1,04 |
| yi | 6,41 | 7,53 | 7,46 | 5,52 | 5,77 | 5,56 | 5,92 | 5,62 | 6,42 | 7,85 | 3,72 | 4,30 |
Продолжение таблицы 4.1.
| i | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| xi | 1,08 | 1,22 | 0,86 | 1,33 | 1,01 | 1,09 | 0,62 | 1,47 |
| yi | 4,20 | 4,79 | 3,57 | 4,99 | 3,73 | 4,04 | 3,08 | 5,43 |
Для заданных значений х и у определить:
коэффициент корреляции r, коэффициенты регрессии у на х и выяснить значимость отличая от нуля коэффициента корреляции.
Вычисляем:
, 
, 
, 
.
, 
, 
,
.
, 
, 
, 
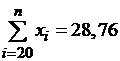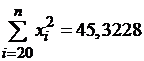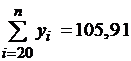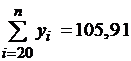
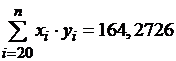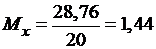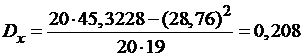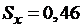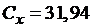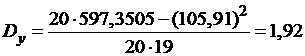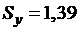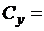26,23.
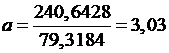b=5,30 - 3,03 ·1,44 = 0,937 
.
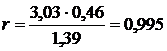Вычисленное значение критерия Стьюдента равно:
.
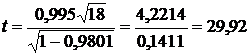Значение критерия, взятое из таблицы при уровне значимости 0,05 равно 2,1. Таким образом, коэффициент корреляции значимо отличается от нуля.
Дата добавления: 2018-06-27; просмотров: 522; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!