Примеры моделей для решения задачи
| Задача | Модель | Интерпретация модели |
| 1 | 2 | 3 |
| 1.Было 6 шаров, из них потеряно 4 шара. Сколько шаров осталось? | 
| Известно: начальное состояние объекта; направленность отношения между начальным и конечным состояниями объекта; числовое значение величины отношения между состояниями объекта. Определить: числовое значение величины конечного состояния объекта |
| 2. Было 4 шара, стало 6 шаров. Что произошло7 | 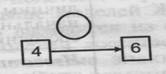
| Известно: начальное состояние объекта; направленность отношения между ними. Определить: характер и числовое значение величины отношений между состояниями объекта. |
| 3. Имеется 6 шаров после того, как выиграно 4 шара. Сколько шаров было до выигрыша? | 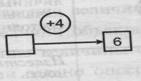
| Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объекта. Определить: числовое значение величины начального состояния объекта |
| 4.Было 6 шаров, стало 4 шара. Что произошло? | 
| Известно: значение величины начального и конечного состояний объекта, направленность отношений между состояниями объекта. Определить: числовое значение величины отношения между состояниями объекта. |
| 5. В первой партии было выиграно 6 шаров, во второй партии было проиграно 4 шара. Что произошло в результате игры? | 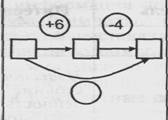
| Известно: направленное отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Определить: значение личины отношения между начальным и конечным состояниями объекта |
| 6. В первое партии было проиграно 6 шаров. Во второй 4 шара. Что произошло в результате игры? | 
| Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 7. В первой партии было проиграно 4 шара. После того как была сыграна вторая партия, всего было потеряно 6 шаров. Что произошло во второй партии | 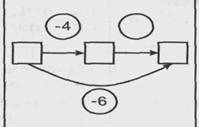
| Известно: направленно отношений между состояниями объекта; числовое значение величин отношений между состояниями, объекта. Определить: значение величины отношения между начальным и конечным состояниями объекта |
| 8. В перовой партии было проиграно 6 шаров. После того как была сыграна вторая партия, всего было потеряно 4 шара. Что произошло во второй партии? | 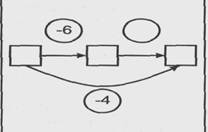
| Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состояниями объекта. Определить: отношения между промежуточным и конечным состояниями объекта |
Необходимо обратить внимание на то, что при построении моделей к задачам 5-8 значение величины на имеет значения для решения задачи. Смысл анализа и решения этих задач заключается в определении характера и количественного выражения отношений между состояниями объекта («выигрыш — проигрыш»).
Таким образом, в моделях, создаваемых для анализа текста и решения задач Ж. Верньё, отображается прежде всего структура задачи, в которой фиксируются состояния объекта, характер и величина отношений между состояниями. Такого рода модели позволяют материализовать схему анализа содержания задачи, ее математический смысл, установить на основе структуры, что является известным, а что необходимо определить, и выстроить последовательность действий для решения задачи.
Использование тех же самых знаково-символических средств (окружность, вектор и др.) может не только приводить к созданию моделей, представляющих структурные компоненты задачи и их отношения, но и наглядно фиксировать последовательность действий в решении задачи. Это отличает их от описанных выше моделей Ж. Верньё, где действия и их последовательность выводятся из схемы отношений. Создание и фиксирование моделей достигается тем, что в язык символов вводятся специальные знаки известных и неизвестных компонентов задачи. Так, известные компоненты обозначаются сплошной линией, а неизвестные — пунктирной.
Один из таких наборов символов может быть представлен в следующем виде:

В зависимости от отношений между величинами объектов модели могут иметь разный вид.
Покажем это на примере так называемых косвенных, или инвертированных, задач, которые, как указывается в методической литературе, являются сложными для решения. Специфика таких задач состоит в том, что при их решении используется арифметическое действие, обратное тому, которое соответствует опорным словами текста задачи.
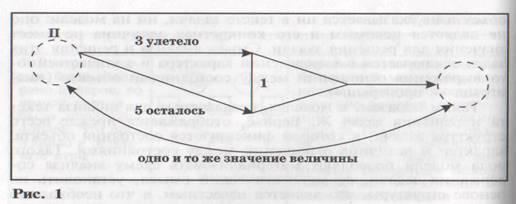
Типичной является задача: «На дереве сидели птички 3 птички улетели, осталось 5. Сколько птичек сидело на дереве?» Ошибкой многих учащихся начальной школы при решении таких задач является то, что они ориентируются на опорное слово «улетели» и поэтому используют вычитание (3 из 5), а не отношение между данными, которое привело бы их к правильному решению. Эти трудности могут быть снятья через построение моделей с использованием указанной выше* символики. Рассмотрим, например, модель на рисунке 1.
В данной задаче объект один — птички. Количество сидящих на дереве птиц (значение искомой величины) неизвестно. Оно представлено на модели двумя пунктирными окружностями: первая обозначает объект (искомое значения величины объекта), вторая — результат действия (тоже искомое значение величины объекта). Задача решается с помощью действия сложения, которое выбирается на основе восстановления сюжетной ситуации, описанной в тексте.
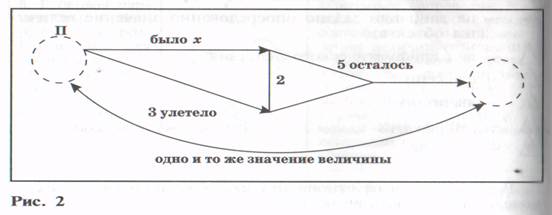
Эта задача может иметь такую модель (см. рис. 2).
В соответствии с этой моделью неизвестное будет находиться путем решения уравнения х — 3 = 5.
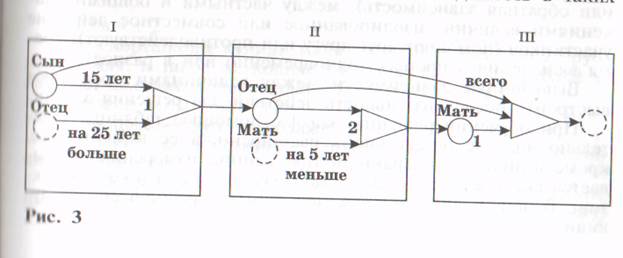
Выявление последовательности действий, необходимых для получения ответа на вопрос задачи, легче осуществлять с помощью рассматриваемых моделей. Например, модель задачи: «Сыну 15 лет. Отец на 25 лет старше сына. Мать на 5 лет младше отца. Сколько лет им вместе?» — будет выглядеть как на рисунке 3.
В данной задаче три объекта: сын, отец, мать. На схеме структура отношений между объектами и последовательность решения задачи представлена в виде трех блоков I, II, III. В первом блоке записаны данные о первых двух объектах: - 15 лет, отец — на 25 лет старше. Пунктирные линии показывают, что возраст отца неизвестен, треугольник с цифрой 1 — способ его нахождения — сложение. Это будет первое действие: 15 + 25 = 40.
Второй блок включает данные о возрасте отца, определенном в результате первого действия, заданном возрасте матери (на 5 лет моложе отца) и способе его нахождения — вычитание: 40 — 5 = 35. Это второе действие.
Третий блок, помимо результата второго действия (возраст матери), включает данные первых двух блоков — возраст сына и отца и способ нахождения ответа.
Рассмотренные знаково-символические средства позволяют создавать модель структуры задачи, включающей объекты, характеризующие их величины, соответствующие им числовые значения (данные и искомые), и фиксировать или выводить действия, необходимые для ответа на вопрос задачи.
Таким образом, при переводе текста задачи на язык материки могут быть использованы схемы (модели) различной степени сложности: от простых с минимальным числом объектов и отношений до сложных. Необходимость в таких схемах выступает отчетливо, когда последовательность выполнения действий по решению задачи расходится с явной структурой задачи или эта структура сложна и открывает miJj гие и разные возможности решения.
Наряду с описанными выше способами в практике обучения широко используется табличный способ представление содержания задачи. Он чаще всего применяется для задач разнородными величинами, когда часть из них является переменными, связываемыми постоянной величиной. Это, как правило, задачи на «процессы».
При создании таблицы фактически реализуются те же этапы учебного моделирования, которые были указаны выше.
I. Анализ текста задачи.
1. Определение вида процесса: движение, работа, купля/продажа.
2. Выделение величин этого процесса и соответствующих им единиц измерения: движение — скорость, время, путь; работа — общий объем, время выполнения, объем работы за определенное время; купля/продажа — цена, стоимость, количество.
П. Составление таблицы.
1. В столбце фиксируются значения величин; количество величин определяет количество столбцов.
2. В строках фиксируются участники (объекты) и этапы процесса; количество строк определяется числом участников и этапов процесса (например, первая покупка, вторая покупка, периоды работы и т. п.).
3. Вычерчивание таблицы, в которой записывается название столбцов и строк.
4. Заполнение таблицы. В соответствующие клетки таблицы вписываются известные данные (числовые значения вели- \ чин), обозначаются неизвестные (х, ?).
III. Работа с таблицей.
На основе данных, представленных в таблице, выделяются функциональные отношения между величинами (прямая или обратная зависимость); между частными и общими значениями величин; изолированное или совместное действие участников (помогают друг другу или противодействуют); время включения в процесс (одновременно или в разное).
Выявленные зависимости между величинами позволяя выстроить последовательность действий для решения задачи
При обучении решению задач с помощью таблицы желательно вначале использовать расширенный ее вариант, где, кроме величин, их характеристик, единиц измерения, указывается вид процесса и дается обозначение участников (объектов). В общем виде таблица может быть представлена следующим образом (табл. 10):
Таблица 10
Дата добавления: 2018-05-31; просмотров: 2508; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
