Определение вибровозмущающих сил
Распределение сил по элементам определенной в п. 1 системы, вызываю-щих вибрацию в ней, определяется электродинамическим взаимодействием токов (1.3), протекающих по указанным элементам [2].
Рассмотрим два элемента с токами  и
и 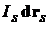 , протекающими в сис-теме по проводникам с различными номерами
, протекающими в сис-теме по проводникам с различными номерами 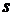 и
и 
 через сечения
через сечения  и
и 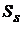 , проведенные через точки
, проведенные через точки 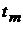 и
и 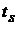 соответственных проводников. В соответствии с ранее определенной параметризацией, пола-гаем, что указанные точки располагаются на соответственных осях указанных проводников и рассматриваются в координатных осях, связанных с этими проводниками так, что
соответственных проводников. В соответствии с ранее определенной параметризацией, пола-гаем, что указанные точки располагаются на соответственных осях указанных проводников и рассматриваются в координатных осях, связанных с этими проводниками так, что 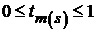 [1]. В силу принятого допущения о равно-мерном распределении токов по сечениям проводников в рассматриваемой системе, электродинамическое воздействие элемента тока
[1]. В силу принятого допущения о равно-мерном распределении токов по сечениям проводников в рассматриваемой системе, электродинамическое воздействие элемента тока 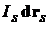 на элемент
на элемент  в каждый момент времени описывается силой
в каждый момент времени описывается силой 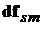 , действующей в этот момент на элемент объема
, действующей в этот момент на элемент объема 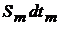 , находящийся вблизи точки
, находящийся вблизи точки 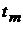 про-водника с номером
про-водника с номером  , со стороны элемента объема
, со стороны элемента объема 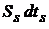 проводника с номе-ром
проводника с номе-ром 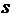 , располагающимся вблизи точки
, располагающимся вблизи точки 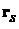 указанного проводника [3]:
указанного проводника [3]:
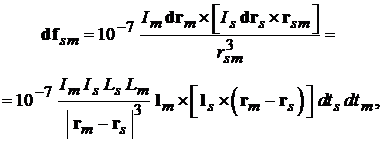 (2.1)
(2.1)
где мгновенные значения токов и длины измеряются в А и м, соответственно; сила 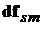 приложена в точке
приложена в точке 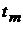 и измеряется в Н.
и измеряется в Н.
Результирующее воздействие проводника с номером 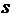 на проводник с номером
на проводник с номером  в точке
в точке 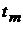 в рассматриваемый момент времени должно тогда определяться силой
в рассматриваемый момент времени должно тогда определяться силой 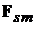 , точкой приложения которой является точка
, точкой приложения которой является точка 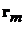 , а на-правление и величина находятся в результате векторного сложения всех уси-лий (2.1), образующихся от непрерывного перемещения вдоль проводника с номером
, а на-правление и величина находятся в результате векторного сложения всех уси-лий (2.1), образующихся от непрерывного перемещения вдоль проводника с номером 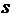 . Поэтому в системе координат, связанной с внешним наблюдателем получаем
. Поэтому в системе координат, связанной с внешним наблюдателем получаем
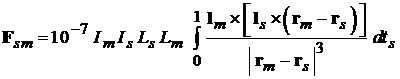 . (2.2)
. (2.2)
Коллективное воздействие в каждый момент времени всех проводников с номерами 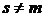 на элемент объема
на элемент объема 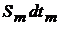 , находящийся вблизи точки
, находящийся вблизи точки 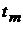 проводника с номером
проводника с номером  , следует рассматривать как результат наложения друг на друга отдельных воздействий проводников с номерами
, следует рассматривать как результат наложения друг на друга отдельных воздействий проводников с номерами 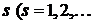
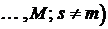 :
:
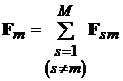 . (2.3)
. (2.3)
Преобразуем выражение (2.2). Воспользовавшись формальным определением векторного произведения двух векторов 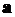 и
и 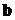
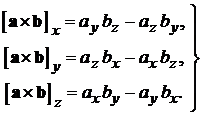 ,
,
а также (1.1), получаем:
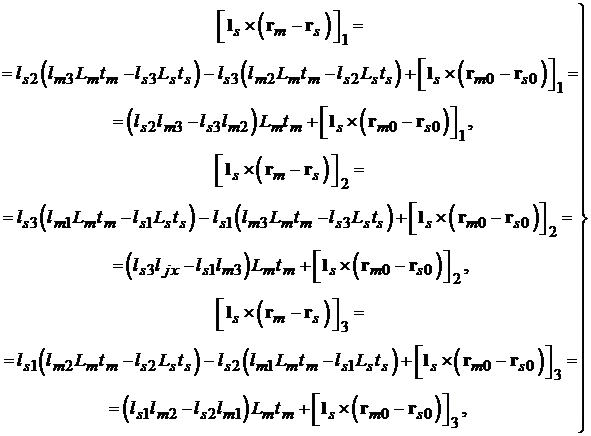
т.е.
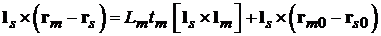 ,
,
а это означает, что
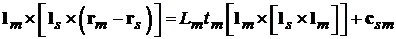 ,
,
где
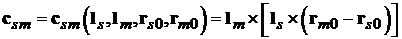 (2.4)
(2.4)
Так как
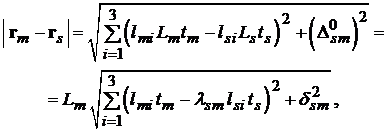
где
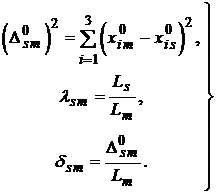 , (2.5)
, (2.5)
то из (2.2) получаем:
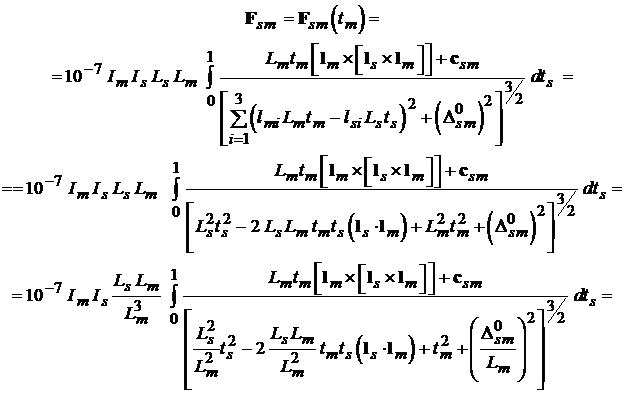
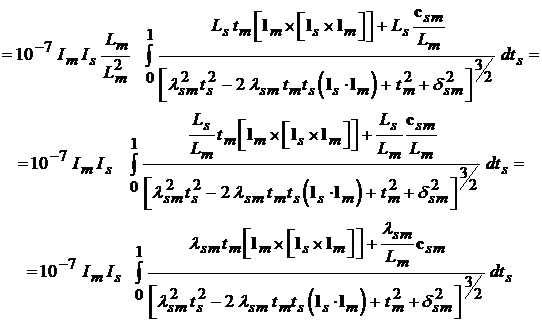
Поэтому
 (2.6)
(2.6)
где
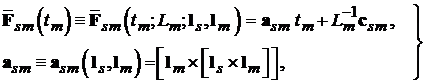 (2.7)
(2.7)
и
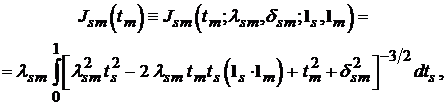 (2.8)
(2.8)
а вектор 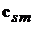 находится из (2.4).
находится из (2.4).
Направление действия силы 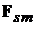 определяется направлением вектора
определяется направлением вектора 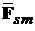 . Нетрудно видеть, что этот вектор лежит в плоскости, перпендикулярной оси проводника с номером
. Нетрудно видеть, что этот вектор лежит в плоскости, перпендикулярной оси проводника с номером  . Действительно, согласно (2.7) направление вектора
. Действительно, согласно (2.7) направление вектора 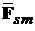 определяется направлением векторов
определяется направлением векторов 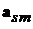 и
и 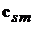 . Но, в силу (2.4) и (2.7), эти векторы перпендикулярны вектору
. Но, в силу (2.4) и (2.7), эти векторы перпендикулярны вектору 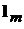 , что и доказывает высказанное утверждение.
, что и доказывает высказанное утверждение.
Используя формулу для двойного векторного произведения [4]
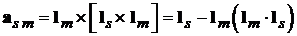 ,
,
получим для координатных составляющих  вектора
вектора 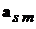 в системе координат, связанной с внешним наблюдателем, выражение
в системе координат, связанной с внешним наблюдателем, выражение
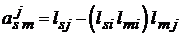 . (2.9)
. (2.9)
в котором использовано правило суммирования Эйнштейна, а  и
и 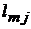 - направляющие косинусы векторов
- направляющие косинусы векторов 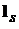 и
и 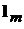 .
.
Применяя формулу для двойного векторного произведения к постоянной 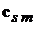 , находим, что
, находим, что
 ,
,
т. е. координатные составляющие этого вектора в системе координат, связанной с внешним наблюдателем, равны
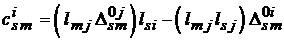 (2.10)
(2.10)
где 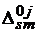 - соответствующие координаты вектора
- соответствующие координаты вектора 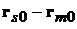 .
.
2.2 Вычисление интеграла 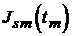
Интеграл в правой части (2.8) сводится к табличным [5]. Пусть
 ,
,
тогда имеем
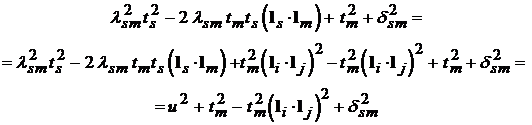
Поэтому

где
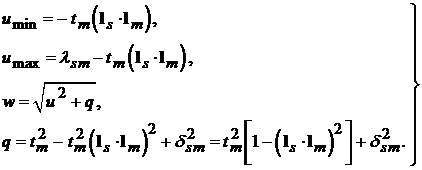
Условия 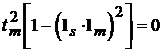 и
и 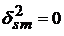 одновременно выполняться не могут в силу того, что первое из них может иметь место только в двух случаях:
одновременно выполняться не могут в силу того, что первое из них может иметь место только в двух случаях:
a) когда проводники с номерами 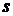 и
и  параллельны;
параллельны;
b) когда рассматривается начальная точка проводника с номером  ;
;
второму же условию соответствует полное совпадение в координатных осях внешнего наблюдателя начальных точек проводников с номерами 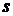 и
и  . Поэтому всегда
. Поэтому всегда 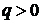 .
.
Воспользовавшись[5], получаем при 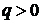
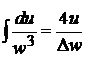 ,
,
где 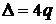 . Поэтому
. Поэтому
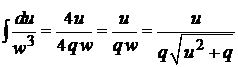
Отсюда
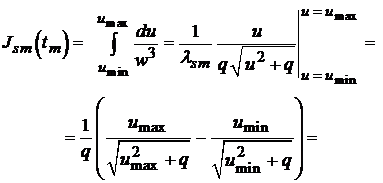

Нетрудно видеть, что подкоренные выражения в знаменателях последней формулы ни при каких реально допустимых значениях параметров и переменной 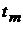 не обращаются в нуль. Действительно, например,
не обращаются в нуль. Действительно, например, 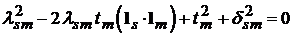 только в том случае, когда
только в том случае, когда 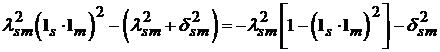 равно нулю. Но это выражение всегда отрицательно.
равно нулю. Но это выражение всегда отрицательно.
Таким образом, рассматриваемый интеграл определяется выражением
 (2.11)
(2.11)
Используя (2.11), находим формулу для определения сил 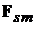 в виде:
в виде:
 . (2.13)
. (2.13)
Из (2.13) и (2.7) следует, что направления сил 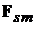 определяются
определяются
Дата добавления: 2018-05-30; просмотров: 169; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
