Задание 8 № 27502 (решено неверно или не решено)
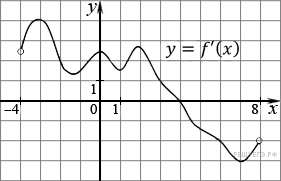 На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
Решение.
Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.
Ответ: 4.
Задание 9 № 904 (решено неверно или не решено)
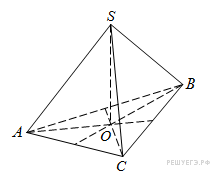 В правильной треугольной пирамиде
В правильной треугольной пирамиде  медианы основания
медианы основания  пересекаются в точке
пересекаются в точке  . Площадь треугольника
. Площадь треугольника 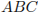 равна 2; объем пирамиды равен 4. Найдите длину отрезка
равна 2; объем пирамиды равен 4. Найдите длину отрезка 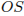 .
.
Решение.
отрезок 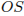 высотой треугольной пирамиды
высотой треугольной пирамиды 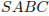 , ее объем выражается формулой
, ее объем выражается формулой 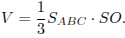
Таким образом, 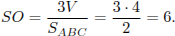
Ответ: 6.
Задание 10 № 1025 (решено неверно или не решено)
В блюде 35 пирожков: 9 с мясом, 12 с яйцом и 14 с рыбой. Катя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с рыбой.
Решение.
вероятность того, что пирожок окажется с рыбой равна
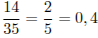 .
.
Ответ: 0,4.
Задание 11 № 27127 (решено неверно или не решено)
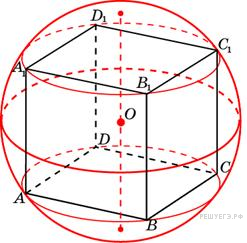 Около куба с ребром
Около куба с ребром 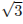 описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на  .
.
Решение.
Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:
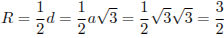 .
.
Поэтому объем шара равен
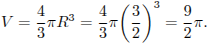
Тогда
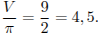
Ответ: 4,5.
Задание 12 № 27966 (решено неверно или не решено)
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой 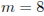 кг и радиуса
кг и радиуса 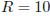 см, и двух боковых с массами
см, и двух боковых с массами 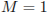 кг и с радиусами
кг и с радиусами 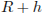 . При этом момент инерции катушки относительно оси вращения, выражаемый в
. При этом момент инерции катушки относительно оси вращения, выражаемый в 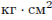 , даeтся формулой
, даeтся формулой 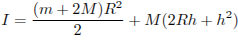 . При каком максимальном значении
. При каком максимальном значении 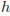 момент инерции катушки не превышает предельного значения 625
момент инерции катушки не превышает предельного значения 625 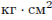 ? Ответ выразите в сантиметрах.
? Ответ выразите в сантиметрах.
Решение.
Задача сводится к нахождению наибольшего решения неравенства 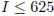 км при заданных значениях параметров
км при заданных значениях параметров 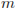 ,
, 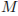 и
и 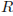 :
:
|
|
|
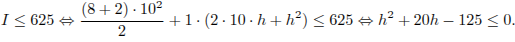
Решая квадратное неравенство методом интервалов, получим 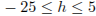 . Наибольшее решение двойного неравенства — число 5.
. Наибольшее решение двойного неравенства — число 5.
Ответ: 5.
Задание 13 № 99614 (решено неверно или не решено)
Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Решение.
Первый мастер выполняет 1/12 работы в час, а второй — 1/6 работы в час. Следовательно, работая вместе, мастера выполняют 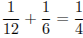 работы в час. Поэтому всю работу мастера выполнят за 4 часа.
работы в час. Поэтому всю работу мастера выполнят за 4 часа.
Другое рассуждение.
Время работы равно отношению объёма к скорости её выполнения. Поэтому два мастера, работая вместе, выполнят заказ за 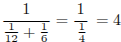 часа.
часа.
Ответ: 4.
Задание 14 № 77470 (решено неверно или не решено)
|
|
|
Найдите наибольшее значение функции 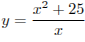 на отрезке
на отрезке 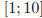 .
.
Решение.
Найдем производную заданной функции:
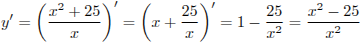 .
.
Производная обращается в нуль в точках 5 и −5, заданному отрезку принадлежит только число 5. Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:
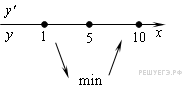
Наибольшим значением функции на заданном отрезке будет наибольшее из чисел 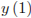 и
и 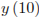 . Найдем их:
. Найдем их:
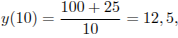
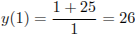 .
.
Ответ: 26.
Проверка части С
Задание С1 № 484548
| Критерии оценивания выполнения задания | Баллы |
| Уравнение решено верно | 2 |
| Корни числителя найдены верно, но само уравнение решено неверно | 1 |
| Все прочие случаи | 0 |
| Максимальный балл | 2 |
Решите уравнение 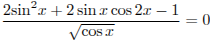 .
.
Решение.
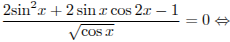

Решим уравнение 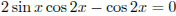 :
:
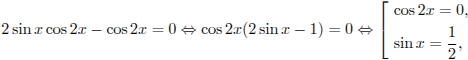
откуда
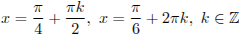 .
.
Из найденный решений условию (*) удовлетворяет только 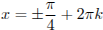 и
и 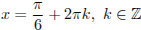 .
.
Ответ: 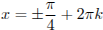 ,
, 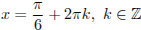 .
.
Задание С2 № 484562
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
В кубе 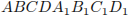 найдите косинус угла между плоскостями
найдите косинус угла между плоскостями 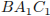 и
и 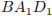 .
.
|
|
|
Решение.
Пусть точка O — центр куба, а M — середина  .
. 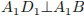 , а MO — средняя линия треугольника
, а MO — средняя линия треугольника 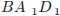 , поэтому
, поэтому 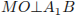 . Треугольник
. Треугольник 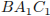 — равносторонний,
— равносторонний, 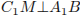 , следовательно, искомый угол равен углу
, следовательно, искомый угол равен углу 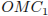 .
.
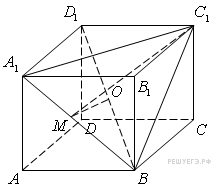 Найдем стороны треугольника
Найдем стороны треугольника  . Из треугольника
. Из треугольника 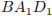 , находим
, находим  из треугольника
из треугольника 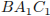 находим
находим
 .
.  ,
,
поскольку O — середина диагонали 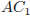 . Теперь применим к треугольнику
. Теперь применим к треугольнику 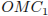 теорему косинусов:
теорему косинусов:
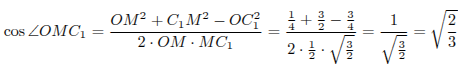
Ответ: 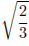 .
.
Задание С3 № 484587
| Содержание критериев оценивания задачи С3 | Баллы |
| Обоснованно получен верный ответ. | 3 |
| При верной последовательности рассуждений получен ответ, неверный только из-за вычислительной ошибки или описки. | 2 |
| Получен ответ, отличающийся от верного только конечным числом точек. | 1 |
| Все прочие случаи. | 0 |
Решите неравенство 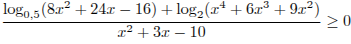 .
.
Решение.

Сделав замену переменной 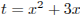 , получаем:
, получаем:
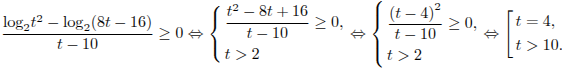
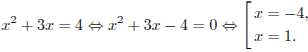
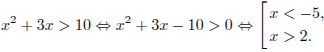
Ответ:  .
.
Задание С4 № 484623
| Критерии оценивания выполнения задания | Баллы |
| 3 | |
| 2 | |
| 1 | |
| 0 | |
| Максимальный балл | 3 |
На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ABP, проведённую из вершины A, если известно, что сторона квадрата равна 1.
|
|
|
Решение.
Пусть точки Р и А лежат по одну сторону от прямой CD (рис. 1). Треугольник BCP — равнобедренный (BC = CD = CP = 1), поэтому
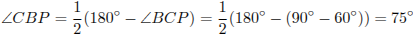 ,
,
значит,
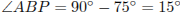 .
.
 Пусть AH — высота треугольника ABP. Из прямоугольного треугольника ABH находим, что
Пусть AH — высота треугольника ABP. Из прямоугольного треугольника ABH находим, что
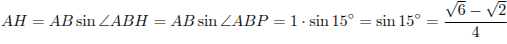 Пусть теперь точки P и A лежат по разные стороны от прямой CD (рис.2). Треугольник BCP — равнобедренный (BC = CD = CP = 1), поэтому
Пусть теперь точки P и A лежат по разные стороны от прямой CD (рис.2). Треугольник BCP — равнобедренный (BC = CD = CP = 1), поэтому
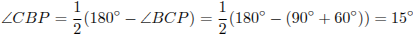 ,
,
значит, 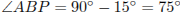

Из прямоугольного треугольника ABH находим, что
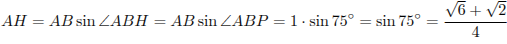 .
.
Ответ: 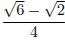 или
или 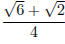 .
.
Задание С5 № 484645
| Содержание критериев оценивания задачи С5 | Баллы |
| Обоснованно получен верный ответ. | 4 |
| Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку. | 3 |
| Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки. | 2 |
| Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. | 1 |
| Все прочие случаи. | 0 |
Найдите все значения параметра а, при каждом из которых система 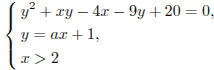 имеет единственное решение.
имеет единственное решение.
Решение.
Преобразуем исходную систему:
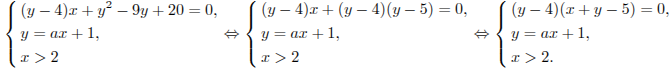
Уравнение 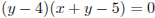 задает пару пересекающихся прямых
задает пару пересекающихся прямых 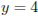 и
и 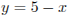 .
.
Система 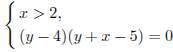
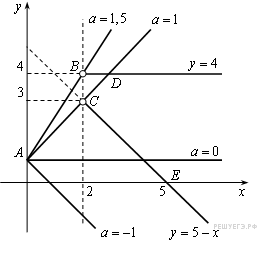
задает части этих прямых, расположенные правее прямой 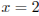 , т. е. лучи DB и CE (без точек B и С), см. рис.
, т. е. лучи DB и CE (без точек B и С), см. рис.
 Уравнение
Уравнение 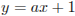 задает прямую m с угловым коэффициентом a, проходящую через точку
задает прямую m с угловым коэффициентом a, проходящую через точку 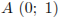 . Следует найти все значения а, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и СЕ.
. Следует найти все значения а, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и СЕ.
а) Прямая АB задается уравнением 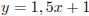 . Поэтому при
. Поэтому при 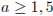 прямая m не пересечет ни луч BD, ни луч СЕ.
прямая m не пересечет ни луч BD, ни луч СЕ.
б) Прямая АС задается уравнением 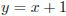 . Поэтому при прямая m пересечет луч BD, но не пересечет луч СЕ.
. Поэтому при прямая m пересечет луч BD, но не пересечет луч СЕ.
в) При 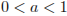 прямая m пресечет и луч BD, и луч СЕ.
прямая m пресечет и луч BD, и луч СЕ.
г) Наконец, при 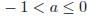 прямая m пересечет только луч СЕ, а при
прямая m пересечет только луч СЕ, а при 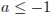 она не пересечет ни луч BD, ни луч СЕ.
она не пересечет ни луч BD, ни луч СЕ.
Ответ: 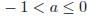 ,
, 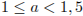 .
.
Задание С6 № 484667
| Критерии оценивания выполнения задания | Баллы |
| 4 | |
| 3 | |
| 2 | |
| 1 | |
| 0 | |
| Максимальный балл | 4 |
Найдите все тройки натуральных чисел k, m и n, удовлетворяющие уравнению  .
.
Решение.
1. Так как 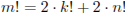 , то
, то 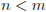 и
и  .
.
2. Пусть  , тогда
, тогда 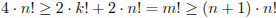 , откуда
, откуда 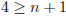 и
и 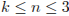 .
.
3. Пусть  , тогда
, тогда 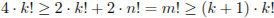 , откуда
, откуда  и
и  .
.
4. Далее конечным перебором значений 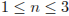 ,
, 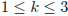 находим все решения.
находим все решения.
| n | k | 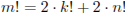
| m |
| 3 | 3 | 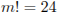
| 4 |
| 3 | 2 | 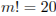
| нет решений |
| 3 | 1 | 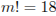
| нет решений |
| 2 | 3 | 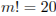
| нет решений |
| 2 | 2 | 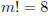
| нет решений |
| 2 | 1 | 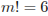
| 3 |
| 1 | 3 | 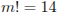
| нет решений |
| 1 | 2 | 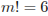
| 3 |
| 1 | 1 | 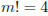
| нет решений |
Ответ: 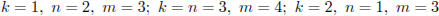 .
.
Конец формы
Дата добавления: 2018-06-27; просмотров: 498; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
