Определители второго и третьего порядков

Понятие множества

Понятия множества и его элемента относятся к числу первичных, неопределяемых понятий математики. К таким же понятиям относятся точка, прямая линия и др. Вместо определения такого понятия приходится обходиться его описанием. Создатель теории множеств Георг Кантор в 1872 году описал понятие множества, как «объединения в одно целое объектов, хорошо различаемых нашей интуицией или нашей мыслью».

Мы будем говорить, что определено некоторое множество М объектов, если указан признак, который позволяет относительно каждого предмета х сказать, принадлежит ли этот предмет множеству М, или нет.

Элементы множеств в дальнейшем будем записывать строчными латинскими буквами, сами множества – прописными. Обозначение aÎ A используется, как краткая запись утверждения: а есть элемент множества А, или: а принадлежит А. Аналогично, обозначение aÏ A используется, как краткая запись утверждения: а не является элементом множества А, или: а не принадлежит А. Множество, не имеющее элементов, называется пустым и обозначается Æ.

Укажем ряд способов задания множеств. Во-первых, можно просто перечислить все элементы множества, если этих элементов – конечное число, т.е. если множество конечное. Например, множество, состоящее из двух чисел, 0 и 1. В этом случае используется обозначение {0,1}. Для произвольного конечного множества, например, состоящего из различных элементов {a1,…am}, используется обозначение {a1,…am},. Подчеркнём, что в этом обозначении множества элементы a1,…am, должны быть различными, однако они могут быть перечислены в произвольном порядке, например, {1,2,3,4} и {2,1,4,3} - различные обозначения одного и того же множества.4

Можно также указать свойство, которому удовлетворяют элементы рассматриваемого множества. Например, множество действительных чисел, больших 5. Обозначим его {x|x > 5}.

Некоторые множества определяются с помощью указания способа последовательного построения его элементов. Например, x1=1, xn=nxn-1, n=2,3,…

Новые множества можно получать и в результате операций над заданными множествами.

Наиболее часто у нас будут рассматриваться множество R действительных чисел, множество N натуральных чисел, множество Z целых чисел, множество Q рациональных чисел.

Подмножества

Важный способ задания множества – выделение его, как части некоторого основного множества. Основное множество образуется всеми элементами какого-нибудь определённого типа. Например, множество целых чисел, множество простых чисел и т.п.

В качестве примера рассмотрим основное множество целых чисел и выберем в нём те числа, которые делятся на 2, т.е. чётные числа. Мы получили множество чётных чисел, которое является подмножеством основного множества целых чисел.

В общем случае, если все элементы множества А являются также элементами множества B, то мы говорим, что А есть подмножество B , или А включено в B , и обозначаем это так: A Ì B .

Если оказалось, что одновременно A Ì B и B Ì A, то эти множества называются равными, что обозначается A = B . Проще говоря, равные множества состоят из одних и тех же элементов.

Из того, что A Ì B и B Ì C следует, что B Ì C (т.е. отношение включения множеств является транзитивным).

Определение множества

В математике некоторые понятия являются первичными, неопределяемыми. К ним относятся понятия натурального числа, точки, прямой и т. д.

Одним из таких неопределяемых понятий является понятие «множество». Этому понятию нельзя дать формального определения, которое не сводилось бы просто к замене слова «множество» его синонимами «совокупность», «набор элементов» и т. п. Множества можно составлять на основе самих различных признаков из самых разнообразных объектов (которые в дальнейшем будем называть элементами множества). Множество можно задать, указывая, например, некоторое свойство объектов, образующих множество, правило построения элементов множества и т. д. Можно говорить не только о множествах, элементами которых являются материальные объекты, но и о множествах, элементы которых — некоторые абстрактные понятия (числа, геометрические фигуры, символы и т. п.).

Понятие «множество» не следует понимать буквально и толковать его как совокупность, содержащую «много» элементов. Под множеством также понимается совокупность объектов, которая может состоять, например, из одного, двух и т. д. элементов. Более того, оказывается удобным считать множеством даже пустое множество, т. е. множество, не содержащее ни одного элемента. Рассматривать пустое множество необходимо хотя бы только потому, что, когда мы определяем тем или иным способом множество, мы можем и не знать заранее, содержит ли оно хотя бы один элемент.

Множества чаще всего обозначаются прописными буквами латинского алфавита A, В, ..., X, а их элементы — малыми буквами: а, b, ..., х. Пустое множество обозначается специальным символом Ø.

Если множество А состоит из п элементов a_1,a₂, …, а₃, то пишут

А = {a₁; a₂; …; а₃}.

Говорят: «элемент а принадлежит множеству А»—и записывают: а 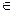А или А 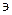а (А содержит а); запись а А означает, что элемент а не принадлежит множеству А.

Любое множество А имеет в качестве своих подмножеств пустое множество и само множество А.

Определение.Под множеством понимается совокупность (собрание, набор) некоторых объектов. Объекты, образующие множество, называются элементами или точками этого множества. Множества обозначаются прописными буквами, а их элементы – строчными. Принадлежность или непринадлежность элемента множеству выглядит так: аÎ А, bÏ В.

Например, если А – множество двузначных натуральных чисел, то 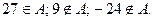Множество русских гласных букв, которые не могут находиться в начале слова, содержит единственный элемент – «ы». Таким образом, множества могут содержать ограниченное число элементов.

Множество, не содержащее ни одного элемента, называется пустым и обозначается Æ.

Пример

Множество девятируких студентов является пустым.

Задание 1.1.1. Определите, какие из чисел –11,5; 0;

принадлежат множеству В положительных чисел. Задание 1.1.2. Приведите примеры пустого множества и множества, содержащего единственный элемент.

Если множество В состоит из части элементов множества А, то множество В называется подмножеством множества А и обозначается .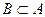

Пример

Множество работников младшего медицинского персонала составляет подмножество множества сотрудников медицинских учреждений. Если рассмотреть числовые множества 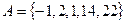и 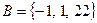, то второе множество будет подмножеством первого. Но если хотя бы один элемент множества В не является элементом множества А, то подмножественность не выполняется.

Пример

Пусть А — множество рациональных чисел, В — множество натуральных чисел. В этом случае В 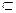А.

Если для двух множеств А и В одновременно справедливы утверждения А 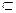В и В 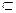А, то множества А и В состоят из одних и тех же элементов. Такие множества А и В называют равными (или совпадающими) и пишут

А = В.

Непустое подмножество В множества А называется собственным, если В не совпадает с А.

Операции над множествами

Обозначение множеств и их элементов. Равенство множеств.

Подмножество ( включение ). Сумма ( объединение ) множеств.

Произведение ( пересечение ) множеств. Разность ( дополнение )

множеств.Симметричная разность множеств. Свойства

операций над множествами.

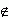Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a R означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут a R .

Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .

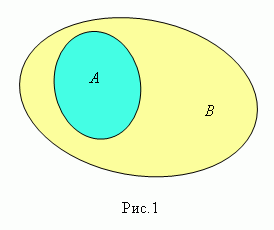
Говорят, что множество А содержится в множестве В ( рис.1 ) или множество А является подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: 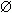А и А А .

Сумма ( объединение ) множеств А и В ( пишется А В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е А В тогда и только тогда, когда либо е А ,либо е В .

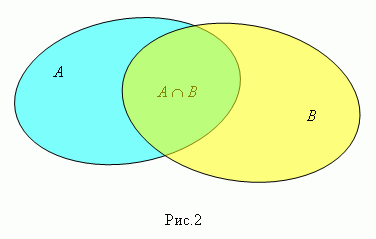
Произведение ( пересечение ) множеств А и В ( пишется А В , рис.2 ) есть множествоэлементов, каждый из которых принадлежит и А , и В. Таким образом, е А В тогда и только тогда, когда е А и е В .

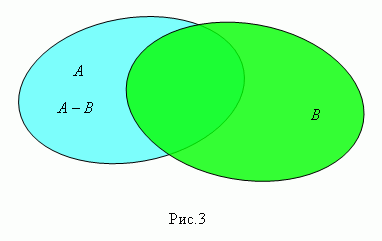
Разность множеств А и В ( пишется А – В , рис.3 ) есть множествоэлементов, которыепринадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется А \ В ) есть множество:

А \ В = ( А – В ) 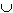( В – А ).

Свойства операций над множествами:

П р и м е р ы.

1. Множество детей является подмножеством всего населения.

2. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.

3. Объединением множества рациональных чисел с множеством иррациональных чисел является множество действительных чисел.

4. Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.

Определители второго и третьего порядков

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

Определитель не изменяется при транспонировании, т.е.

При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

Определитель, имеющий нулевую строку, равен 0.

Определитель, имеющий две равные строки, равен 0.

Определитель, две строки которого пропорциональны, равен 0.

При перестановке двух строк определителя он умножается на –1.

Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Свойства определителей

С в о й с т в о 1. (о разложении определителя по элементам строки или столбца). Определитель равен сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения.

С в о й с т в о 2. При транспонировании матрицы ее определитель не меняется.

С в о й с т в о 3. Общий множитель элементов какого-либо столбца или какой-либо строки можно вынести за знак определителя.

Другими словами, если определитель умножается на число, то умножаются на это число все элементы какой-нибудь строки или какого-нибудь столбца.

С в о й с т в о 4. Определитель, у которого все элементы какой-нибудь строки или какого-нибудь столбца равны нулю, равен нулю.

С в о й с т в о 5. Если в определителе поменять местами две любые строки (столбца), то знак определителя изменится.

С в о й с т в о 6. Если в определителе элементы какой-либо строки (столбца) равны или пропорциональны соответствующим элементам другой строки (столбца), то он равен нулю.

С в о й с т в о 7. Если в определителе элементы какой-нибудь строки (столбца) представляют собой суммы двух слагаемых, то он может быть разложен на сумму двух соответствующих определителей.

С в о й с т в о 8. Если к элементам некоторого строки (столбца) прибавить соответствующие элементы другого строки (столбца), умноженные на любой общий множитель, то величина определителя при этом не изменится.

С в о й с т в о 9. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю.

С в о й с т в о 10. Определитель произведения квадратных матриц равен произведению определителей этих матриц, т. е. если А и В квадратные матрицы одного порядка, то |A∙B| = |A|∙|B|.

Аналогично можно ввести понятия определителей четвертого, пятого,…, n-порядков, их миноры и алгебраические дополнения и показать, что они обладают рассмотренными выше свойствами.

Дата добавления: 2018-05-13; просмотров: 318; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!