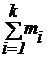Часть 3. Основы теории вероятностей и математической статистики
Nbsp; Петровский колледж
ЗАОЧНОЕ ОТДЕЛЕНИЕ
Методическое пособие
для выполнения контрольныхзаданий по математике
для студентов заочного отделения
средних специальных учебных заведений
специальность 42.02.01 «Реклама»
Гармашов А.В.
Санкт-Петербург - 2015
ББК 65.9(2)27 К90
Методическое пособие для выполнения контрольных заданий по математике
Автор:
А.В.Гармашов, к.ф.-м.н.
- СПб: 2015г., 64с.
Методическое пособие предназначено для выполнения контрольныхзаданий по математике студентами заочного отделения средних специальных учебных заведений. Настоящее пособие составлено в соответстии с действующим Государственным стандартом и типовой программой 2014 года для специальности 42.02.01 «Реклама». По каждому разделу курса математики приведены краткие теоретические сведения. В пособие включены такие разделы как дифференциальное и интегральное исчисления,элементы теории вероятностей, основы математической статистики. В заключение каждого параграфа даны решения типичных примеров и контрольныезадания.
© Петровский колледж, 2015.
Предисловие
Основной целью курса "Математика" является ознакомление студентов с основами современного математического аппарата как средства решения теоретических и практических задач в профессиональной сфере.
Одним из важных этапов подготовки высококвалифицированных специалистов в системе заочного обучения является самостоятельная работа студентов.
|
|
|
Самостоятельная работа студентов-заочников состоит из самостоятельного изучения теоретического материала и выполнения контрольных заданий.
Общие рекомендации для студентов-заочников при изучении курса математики.
Первая часть курса базируется на математических дисциплинах общеобразовательной средней школы.
Основным видом работы студентов-заочников является самостоятельное изучение теоретического материала, решение задач и примеров, самопроверка и выполнение контрольныхзаданий.
Изучениематематики следует начинать с ознакомления с программой.При работе с литературой необходимо строго придерживаться такого порядка изучения материала, который рекомендован в приведенной ниже программе.
При изучении материала целесообразно в специальной тетради вести конспект. В конспект рекомендуется записывать определения, формулировки теорем, формулы.
Изучение теоретического материала должно сопровождаться решением примеров и задач. К выполнению контрольныхзаданий следует приступать только после тщательной проработки необходимого теоретического материала.
|
|
|
Студент выполняет тот вариант контрольной работы, который определяется индивидуальными параметрами.
Выполнение каждой задачи (примера) следует начинать с новой страницы. Решение задач и примеров необходимо излагать подробно, с объяснениями и ссылками на теорию.
Методические указания по выполнению контрольныхзаданий по математике.
Контрольноезадание выполняется в отдельной тетради.Титульный лист контрольногозадания студента заочного отделения заполняется по следующей форме:
| ПЕТРОВСКИЙ КОЛЛЕДЖ ЗАОЧНОЕ ОТДЕЛЕНИЕ Контрольноезадание по математике. Вариант № ______ Студент _______ группы Проверил ____________ Ф.И.О. полностью в родительном падеже _________ |
Для облегчения выполнения контрольного задания студентами-заочниками ниже приводятся краткие теоретические сведения и примеры решения задач по разделам математики, включенным в контрольные задания.
Основы математического анализа.
Часть 1. Дифференциальное исчисление
1.1. Функция. Предел функции
Определение 1. Переменная величина y называется функцией от переменной величины x, если они связаны между собой так, что каждому допустимому значению величины x соответствует единственное, вполне определенное значение величины y.
|
|
|
Определение 2. Совокупность всех значений независимой переменной (аргумента) x, для которых функция y определена, называется областью определения или областью существования функции.
Функцию можно задатьтремяспособами:
а) аналитически с помощью одной или нескольких формул (явно, неявно, параметрически);
б) с помощью таблицы, где для определенных значений аргумента приводятся числовые значения функции;
в) с помощью графика.
К основным элементарным функциям относятся:
1. Степенная функция y=xn, где n - целое число (nÎZ)
а) Для n≥0 областью определения служит (-∞, +∞). Графики степенной функции с n≥0 представляют собой параболы различных порядков.
б) для n<0 областью определения степенной функции служат интервалы (-∞,0)È(0,+∞), а графики представляют собой гиперболы различных порядков.
2. Показательная функция y=аx, где а>0, а≠1.
Областью определения показательной функции является (-∞,+∞). Функция имеет положительные значения и монотонно возрастает от 0 до +∞ при а>1 и монотонно убывает от +∞ до 0 при 0<а<1.
3. Логарифмическая функция y=logax,a>0; a≠1
Областью определения логарифмической функции является (0,+∞), областью значений (-∞,+∞). При а>1 логарифмическая функция строго возрастает, при 0<a<1 - строго убывает. Логарифмическая функция обратна показательной функции.
|
|
|
4. Тригонометрические функции.
а) y=sinx. Область определения функции – (-∞,+∞), множеством значений функции является отрезок [-1,+1]. Функция sinx - нечетная функция при любом x, т.е. sin(-x) = -sinx. Функция sinx - периодическая с основным периодом 2p.
б) y=cosx. Область определения функции (-∞, +∞), множеством значений функции [-1,+1]; y=cosx - четная функция (cos(-x)=cosx), Функция y=cosx - периодическая с основным периодом 2p.
в) y=tgx, y=ctgx. Функции y=tgx и y=ctgx не рассматриваем более подробно, т.к. при описании различных физических процессов они встречаются очень редко.
5. Обратные тригонометрические функции y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Сведений об этих функциях не приводим по той же причине, что и для функций tgx и ctgx.
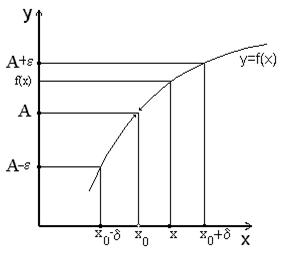
Определение 3. Число А называется пределом функции y=f(x) в точке x0 (при x→x0), если для любого числа ε>0 найдется такое число d(ε)>0, что для любого x≠x0, удовлетворяющего неравенству |x-x0|<d, выполняется соотношение |f(x)-A|<ε.
То, что функция f(x) в точке x0 имеет предел, равный А, обозначают так: 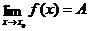
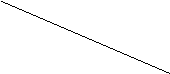
Геометрически существование предела : 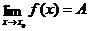 означает, что каково бы ни было число ε›0, найдется d›0 такое, что для всех х, заключенных между точками х0-d и х0+d (кроме, быть может, самой точки х0), график функции y=f(x) лежит в полосе, ограниченной прямыми y=A+ε и y=A-ε. (Рис. 1).
означает, что каково бы ни было число ε›0, найдется d›0 такое, что для всех х, заключенных между точками х0-d и х0+d (кроме, быть может, самой точки х0), график функции y=f(x) лежит в полосе, ограниченной прямыми y=A+ε и y=A-ε. (Рис. 1).
|
Определение 4. Функция y=f(x) называется бесконечно малой при x→x0, если для любого числа ε>0 найдется такое число d>0, что для любого x≠x0, удовлетворяющего неравенству |x-x0|<d, выполняется неравенство |f(x)|<ε.
Иначе говоря, функция y=f(x) называется бесконечно малой при x→x0, если 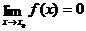 .
.
Теорема о связи понятий бесконечно малой и предела.
1. Если функция f(x) при x→x0 имеет предел, равный числу А, то она может быть представлена в виде суммы предела и бесконечно малой функции, т.е. если 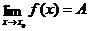 , то f(x)= A+α(x), где α(x) - бесконечно малая при x→x0.
, то f(x)= A+α(x), где α(x) - бесконечно малая при x→x0.
2. Если функция может быть представлена в виде суммы постоянного числа А и бесконечно малой α(x), то число А является пределом функции f(x), т.е. если f(x) = А+ α(x), где А=const, α(x) - бесконечно малая при x→x0, то  .
.
Бесконечно малые функции могут отличаться порядком малости. Порядок малости характеризует "скорость" стремления бесконечно малых к нулю. Бесконечно малую функцию, которая стремится к 0 быстрее другой, называют бесконечно малой высшего порядка малости.
Чтобы сравнить две бесконечно малые α(x) и β(x) по порядку малости, нужно найти предел их отношения.
1. Если 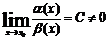 , то α(x) и β(x) одного порядка малости.
, то α(x) и β(x) одного порядка малости.
2. Если  , то α(x) имеет высший порядок малости, чем β(x).
, то α(x) имеет высший порядок малости, чем β(x).
Определение 5. Функция y=f(x) называется бесконечно большой при x®x0, если для любого числа M>0 существует такое число d>0, что для всех x≠x0, удовлетворяющих неравенству |x-x0|<d выполняется неравенство |f(x)|>M.
Обозначается это так: 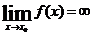
Лемма 1) Если функция f(x)-бесконечно большая при x→x0, то (f(x))-1 бесконечно малая при x→x0.
2) Если α(x)- бесконечно малая функция при x→x0, то (α(x))-1 бесконечно большая при x→x0.
Теоремы о пределах:
Теорема 1. Предел постоянной равен самой постоянной: 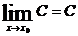
Теорема 2. Предел алгебраической суммы конечного числа функций равен алгебраической сумме их пределов при условии, что эти пределы существуют:
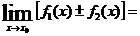

Теорема 3. Предел произведения двух функций равен произведению их пределов, при условии, что эти пределы существуют.
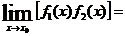
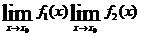
Теорема справедлива для любого конечного числа сомножителей.
Следствие 1: Если 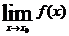 существует при x→x0 и n-натуральное число, то
существует при x→x0 и n-натуральное число, то 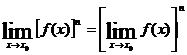
Следствие 2: Постоянный множитель можно вынести за знак предела: 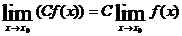
Теорема 4. Предел отношения двух функций равен отношению их пределов, если последние существуют, и предел знаенателя не равен 0.
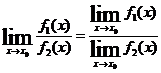 ,если
,если 
Теорема 5. Если функция y=f(g(x)) является сложной функцией, то для всех элементарных функций в области их определения
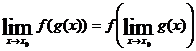
Теорема 6. Если 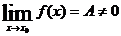 , то в некоторой окрестности точки x0знак функции совпадает со знаком числа A.
, то в некоторой окрестности точки x0знак функции совпадает со знаком числа A.
Первый замечательный предел: 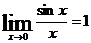
Второй замечательный предел: 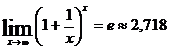
Некоторые приемы вычисления пределов.
Пример 1. Вычислить 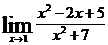
Решение. Вначале найдем предел знаменателя; применяем теоремы 1,2, следствие 1 из (3)

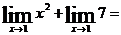

Применяем теоремы 1,2,3,4:
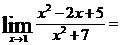
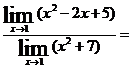
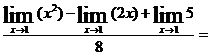
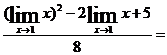
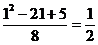 .
.
Пример 2. Вычислить 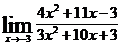
Решение: Непосредственное применение теорем о пределах приводит к неопределенному выражению вида 0/0. Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители, и сократим дробь на множитель (x+3):
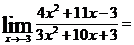
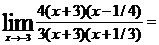
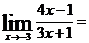
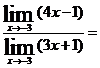
= 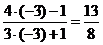
Пример 3. Вычислить 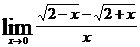
Решение. Непосредственное применение теорем о пределах к числителю дает значение его предела = 0. Предел знаменателя также 0. Получили неопределенное выражение 0/0. Для раскрытия неопределенности числитель и знаменатель данной дроби умножаем на  .
.
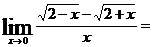
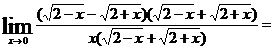 =
= 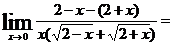

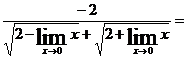 =
= 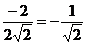
Пример 4. Вычислить 
Решение. Найдем предел знаменателя: 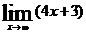 - бесконечно большая величина. Тогда 1/(4x+3) - бесконечно малая при x→∞, значит и 2/(4x+3) бесконечно малая при x→∞, т.е.
- бесконечно большая величина. Тогда 1/(4x+3) - бесконечно малая при x→∞, значит и 2/(4x+3) бесконечно малая при x→∞, т.е. 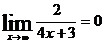
Пример 5. Вычислить 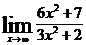
Решение: Применив теоремы о пределах, получим неопределенное выражение вида ∞/∞. Для раскрытия неопределенности числитель и знаменатель дроби почленно разделим на наивысшую степень аргумента в знаменателе:
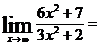
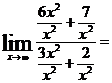
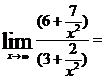
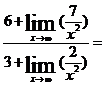
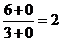
т.к. при x→∞ величины 7/x2 и 2/x2 -бесконечно малые и 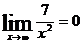 .
.
1.2. Производная и дифференциал функции
Рассмотрим функцию y=f(x).
Определение 1.Разность двух значений аргумента(x0 и x) называется приращением аргумента ∆x: ∆x=x-x0 =>x=x0+∆x.
Определение 2. Разность двух значений функции y0=f(x0) и y=f(x) называется приращением функции y: ∆y=y-y0= f(x)-f(x0)=f(x0+∆x)-f(x0).
Определение 3. Функция y=f(x) называется непрерывной в точке x0, если
1) функция определена в точке x0 и ее окрестности;
2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. 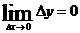
Определение 4. Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.
Все основные элементарные функции непрерывные в своей области определения.
Определение 5. Производной функции y=f(x) в данной точке называется предел (если он существует) отношения приращения функции к вызвавшему его приращению аргумента, когда последнее стремится к нулю.
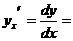
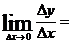
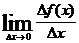
Физический смысл производной состоит в следующем: производная функции y= f(x) по аргументу x есть мгновенная скорость изменения функции при данном значении аргумента, если независимой переменной являетсявремя и есть градиент функции, если независимой переменной является координата.
Геометрический смысл производной состоит в том, что производная функции y=f(x) при данном значении аргумента x равна угловому коэффициенту "k" касательной к графику функции в точке x: f'(x) = tgα = k, где α - угол между касательной к графику в точке x и положительным направлением оси Ox (Рис.2). Уравнение касательной к графику функции y=f(x) в точке М0(x0,y0) можно записать так: y-y0 = k(x-x0) или, учитывая, что k=f'(x0), получим y-y0 = f'(x0)(x-x0).
 y
y
M1y =f (x)
M0 φΔy
Δx
 φαx Рис.2
φαx Рис.2
0 x0x0+Δx
Если функция в данной точке имеет производную, то ее называют дифференцируемой в этой точке, а процесс нахождения производной - дифференцированием функции.
Формулы дифференцирования.
1. Производная постоянной величины равна нулю С'=0.
2. Производная независимой переменной равна 1: X'x =1.
3. Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций:
(U(x) + V(x) - W(x))'x = U'x (x) + V'x(x) - W'x(x)
4. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую: (U(x)·V(x))'x = U'x(x)·V(x) + V'x(x)·U(x)
Следствие: Постоянный множитель можно выносить за знак производной:
(C·U(x))'x= C·U'x(x) или 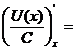
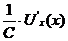
5. Производная функции, представляющей частное двух функций, равна дроби, знаменатель которой равен квадрату знаменателя данной функции, а числитель есть разность между произведениями производной числителя на знаменатель и производной знаменателя на числитель:
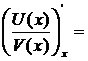
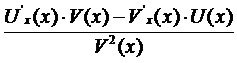
Определение 6: Сложной функцией называется функция, аргументом которой служит функция: y=f(u), где u=g(x), т.е. y=f[g(x)]. Аргумент "u" называют промежуточным, а x - конечным.
6. Производная сложной функции по конечному аргументу равна произведению производной функции по промежуточному аргументу на производную промежуточного аргумента по конечному:
yx'=yu'·ux'.
Формулы дифференцирования основных элементарных функций приведены в приложении.
Производную f''(x) называют производной первого порядка, или первой производной.
Определение 7: Производную от первой производной называют второй производной или производной второго порядка:
y"xx= (yx')'xилиf"(x)= (f'(x))'x
1.3. Дифференциал функции.
Согласно теореме о связи предела и бесконечно малой функции приращение функции y=f(x) можно представить в виде суммы двух слагаемых: ∆y=y'·∆x+α(x)∆x, где α(x) - бесконечно малая при ∆x→0.
Второе слагаемое - бесконечно малая высшего порядка малости в сравнении с первым. Слагаемое y'·∆x составляет главную часть приращения функции.
Определение 8: Главная часть приращения функции, линейная относительно приращения аргумента, называется дифференциалом функции (dy): dy = y'·∆x
Учитывая, что при y=x имеем dx=x'∆x, т.е. dx=∆x, получаем
dy=y'·dx,
т.е. дифференциал функции равен произведению производной функции на дифференциал ее аргумента. Отсюда y'=dy/dx.
Решение типовых задач.
Задача: найти производную функций
а) y=(x5+x+8)·ctg3x
Решение. Воспользуемся правилом 4 дифференцирования произведения двух функций y'=(x5+x+8)'·ctg3x+(x5+x+8)·(ctg3x)'. Далее используем правило 3 дифференцирования суммы и правило 6 дифференцирования сложной функции: (ctgu)'x=-(1/sin2u)·u'x, где u=3x.
Получаем: y'=(5x4+1)∙ctg3x-(x5+x+8)∙ 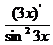 = (5x4+1)∙ctg3x -
= (5x4+1)∙ctg3x - 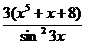 .
.
б) 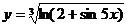
Решение. Представим данную функция в виде степени y=[ln(2+sin5x)]1/3 и применим правило дифференцирования сложной функции:
(un)'x=n·un-1·u'x. В нашем примере u=ln(2+sin5x), n=1/3.
Получаем: y'=1/3 [ln(2+sin5x)]-2/3·[ln(2+sin5x)]'. Далее применим формулу (lnu)'=u'/u, где u=2+sin5x
Тогдаy’ =1/3 [ln(2+sin5x)]-2/3·  .
.
Используем далее правило 3 и формулу: (sinu)'=cosu·u', где u=5x получаем:
y'=1/3 [ln(2+sin5x)]-2/3· 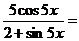
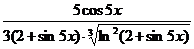 .
.
Задача: найти вторую производную функцииy=e2x+1.
Решение. Найдем y', используя формулу: (eu)'x =eu·u'x
В нашем примере u=2x+1. y'=e2x+1·(2x+1)' = 2e2x+1
y"=(y')'=(2e 2x+1)'=2(e2x+1)'=4e 2x+1.
Задача: найти дифференциал функции 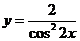 .
.
Решение. Запишем функцию в виде: y=2(cos 2x)-2. Используем правило: dy=y'x·dx.
dy= [2(cos 2x)-2]'·dx=2[(cos2x)-2]'·dx= =-4·(cos2x)-3 (cos2x)'·dx=-4(cos2x)-3·(-sin2x)·(2x)'·dx
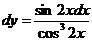 .
.
Задача: Составить уравнение касательной к графику функции y=3x4+7 в точке x0=2.
Решение. Найдем ординату точки касания y0=f(x0): y0=3·24+7=55. Найдем угловой коэффициент касательной k=f'(x0) f'(x)=12x3, f'(2)=12·23=96, т.е. k=96.
Запишем уравнение касательной в виде y=y0=k(x-x0): y-55=96(x-2) или y=96x-137.
1.4. Применение производных и исследование функций
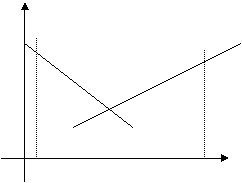
Определение 1. Функция y=f(x) называется возрастающей на интервале (a,b), если для любых двух точек x1 и x2 этого интервала из неравенства x2>x1 следует неравенство f(x2)≥f(x1), т.е. приращение аргумента и приращение функций имеют одинаковые знаки. Если из x2>x1 следует f(x2)>f(x1), то функцию называют строго возрастающей. (рис.3)
Определение 2. Функция y=f(x) называется убывающей на интервале (a,b), если для любых двух точек x1 и x2 этого интервала из неравенства x2>x1 следует неравенство f(x2)≤f(x1), т.е. приращение аргумента и приращение функции имеют противоположные знаки. (рис.3)
 y
y
 yy=f (x) убывающая функция
yy=f (x) убывающая функция
f (x2) возрастающая f (x1)
f (x1) функция f (x2) y=f (x)
0 x1 x2 X 0 x1x2X
Рис.3.
Теорема 1 (о необходимых условиях невозрастания и неубывания функции на интервале)
Если дифференцируемая функция f(x) не убывает на (a,b), то в любой точке этого интервала f''(x)≥0;
Если дифференцируемая функция f(x) не возрастает на (a,b), то в любой точке этого интервала f''(x)≤0.
Если дифференцируемая функция f(x) на (a,b) не изменяется, то ее производная f''(x)=0.
Теорема 2. (о достаточных условиях строгого возрастания и убывания функции на интервале)
Если производная f''(x) функции y=f(x) на интервале (a,b) отрицательна, то функция на этом интервале строго убывает.
Если производная f''(x) функции y=f(x) на интервале (a,b) положительна, то функция на этом интервале строго возрастает.
Если производная f''(x) функции y=f(x) на интервале (a,b) равна нулю, то функция на этом интервале сохраняет постоянное значение.
Определение 3. Значение функции f(x0) называется локальным максимумом функции y=f(x) на интервале (a,b), если существует такая β-определенность ]x0-β,x0+β[ точки x0, что для всех x≠x0 этой окрестности выполняется неравенство: f(x)<f(x0). (рис.4)
Определение 4. Значение функции f(x0) называется локальным минимумом функции y=f(x) на интервале (a,b), если существует такая β-определенность ]x0 -β,x0+ β[ точки x0, что для всех x≠x0 этой окрестности выполняется неравенство: f(x)>f(x0). (рис.4)
Точку x0 называют, соответственно определению 3 (определению 4), точкой максимума (точкой минимума). Максимум и минимум функции называются локальным экстремумом функции.
 y y
y y
f (x0) · f (x) < f (x0) f (x) > f (x0)
f (x) максимум минимум
f (x)
f(x0) ·
0 x0 x x 0 x0xx
Рис. 4.
Теорема 3 (о необходимом условии существования экстремума дифференцируемой функции)
Если функция y=f(x), дифференцируемая на интервале (a,b), имеет в точке x0є(a,b) экстремум, то ее производная в этой точке равна нулю.
Теорема 4 (о достаточных условиях экстремума функции)
Если производная функции y=f(x) в точке x0 обращается в нуль (f'(x0)=0), и при переходе через эту точку в направлении возрастания аргумента меняет знак с плюса на минус, то в точке x0 эта функция имеет максимум; если знак производной меняется с минуса на плюс, то в точке x0 функция имеет минимум; если же при переходе через точку x0 производная f'(x) не меняет знак, то в точке x0 функция экстремума не имеет.
Определение 5. Кривая y=f(x) называется выпуклой на интервале (a,b), если она лежит ниже касательной, проведенной к этой кривой в любой точке x этого интервала (рис. 5).
Определение 6. Кривая y=f(x) называется вогнутой на интервале (a,b), если она лежит выше касательной, проведенной к этой кривой в любой точке x этого интервала (Рис. 5.).

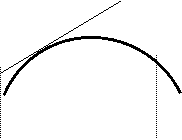
 y y
y y
вогнутость выпуклость
0 a b x 0 a bx
Рис. 5.
Теорема 5 (о достаточных условиях выпуклости и вогнутости кривой)
Если вторая производная f"(x) функции y=f(x) на интервале (a,b) положительна, то график функции на этом интервале вогнутый, а если вторая производная f"(x) отрицательна, то график функции выпуклый.
Определение 7. Точка непрерывной кривой, отделяющая участок выпуклости от участка вогнутости или наоборот, называется точкой перегиба (рис. 6).
 y
y
Рис. 6.
0 x0 x
Теорема 6 (о достаточных условиях наличия точки перегиба)
Если вторая производная f"(x) функции y=f(x) в некоторой точке x0 обращается в нуль и при переходе через нее меняет свой знак на обратный, то точка (x0,f(x0)) является точкой перегиба графика функции.
Правило 1 исследования функции на возрастание, убывание и экстремумы.
1. Указать область определения функции y=f(x).
2. Найти производную y'=f'(x).
3. Составить уравнение f'(x)=0 и найти его корни (критические значения).
4. Разбить область определения критическими значениями аргумента x на интервалы монотонности и найти знак производной на каждом интервале.
5. На основании теоремы 2 сделать вывод о возрастании или убывании функции на интервалах.
6. На основании теоремы 4 сделать вывод о наличии экстремумов в критических точках, разделяющих интервалы монотонности.
Правило 2 исследования функции на выпуклость, вогнутость и наличие точек перегиба.
1. Указать область определения функции y=f(x).
2. Найти вторую производную y"=f"(x).
3. Составить уравнение f"(x)=0 и найти его корни.
4. Разбить область определения функции найденными корнями на интервалы и найти знак второй производной на каждом интервале.
5. На основании теоремы 5 сделать вывод о выпуклости или вогнутости графика функции на интервалах.
6. На основании теоремы 6 сделать вывод о наличии точек перегиба.
Решение типовой задачи.
Задача. Дана функция 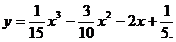
Провести ее исследование на возрастание, убывание, экстремумы, выпуклости, вогнутость и точки перегиба.
Решение. Используем правила 1 и 2.
1. Область определения функции (-∞, +∞).
2. Найдем 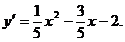
3. Составим уравнение 
Получим квадратное уравнение x2-3x-10=0. Корни этого уравнения x1=-2 и x2= 5 являются критическими точками.
4. Разбиваем область определения функции критическими точками на интервалы монотонности: (-∞,-2); (-2,5); (5,+∞).
5. Выбираем в каждом интервале произвольную точку и определяем в ней знак производной: f'(-3)>0; f'(0)<0; f'(6)>0.
6. Из теоремы 2 следует: на первом и третьем интервалах функция возрастает, а на втором - убывает.
7. Из теоремы 4 следует, что в точке x=-2 функция имеет максимум: ymax=f(-2)= 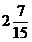 . В точке x=5 функция имеет минимум: ymin=
. В точке x=5 функция имеет минимум: ymin= 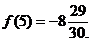
8. Найдем y"= 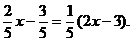
9. 2x-3=0, x=3/2.
10. Точка x=3/2 - разбивает область определения на два интервала:
(-∞,3/2) и (3/2,+∞)
11. Найдем знак второй производной в произвольных точках этих интервалов f"(0)<0; f"(2)>0
12. На основании теоремы 5 делаем вывод: на интервале (-∞,3/2) график функции выпуклый, а на интервале (3/2,+∞) - вогнутый.
13. На основании теоремы 6 получаем: при переходе через точку x=3/2 вторая производная меняет знак. Это значит, что x=3/2 является абсциссой точки перегиба графика. Ордината точки перегиба f(3/2)= -13/4.
Контрольноезадание №1.
Номера задач, соответствующие каждому варианту, определяются последней цифрой электронного пропуска. Допустим, пропуск имеет номер 12304057, следовательно, студенту необходимо решить все задачи, номера которых заканчиваются цифрой7, т.е. задачи 7, 17, 27, 37, ... .
В задачах 1-10 найти заданные пределы.
1. 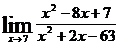 2.
2. 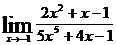
3. 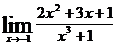 4.
4. 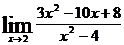
5. 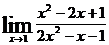 6.
6. 
7. 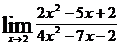 8.
8. 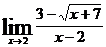
9. 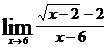 10.
10. 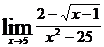
В задачах 11-20 требуется найти производные заданных функций.
11. y=(x5+8x)sin2x 12. y=e2x(x3+ 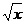 )
)
13. y=(x+1)2tg8x 14. y= 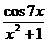
15. y=x3·ctg2x 16. y= 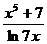
17. y=  18. y=lncos3x
18. y=lncos3x
19. y=aeax+xe-ax 20. y=ex/a·sin(x/a)
В задачах 21-30 требуется найти дифференциалы заданных функций.
21. y= 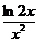 22. y=cos32x
22. y=cos32x
23. y= x·3x 24. y=ln(lnx)
25. y=lntg2x 26. y=sin 3x+5
27. y=ln3(x/3) 28. y=ln(sinx+2cosx)
29. y=sin2x·cos2x 30. y= 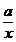 + arctg
+ arctg 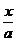
В задачах 31-40 требуется исследовать с помощью производной заданные функции на возрастание, убывание, экстремумы, промежутки выпуклости и вогнутости графика функции и наличие точек перегиба.
31. y = 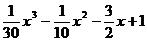 32. y =
32. y = 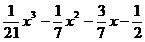
33. y = 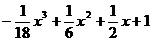 34. y =
34. y = 
35. y = 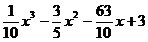 36. y =
36. y = 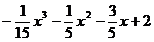
37. y = 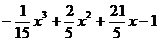 38. y =
38. y = 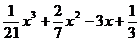
39. y = 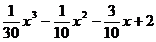 40. y =
40. y = 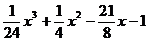
Часть 2. Интегральное исчисление
2.1. Неопределенный интеграл
Определение 1. Первообразной функцией для данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна данной функции f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.
Определение 2. Совокупность первообразных F(x)+C для данной функции f(x) или данного дифференциала f(x)dx называется неопределенным интегралом от функции f(x) и обозначают ∫f(x)dx.
Вычисление интеграла от данной функции называют интегрированием этой функции.
Основные свойства неопределенного интеграла.
10 Дифференциал неопределенного интеграла равен подынтегральному выражению,апроизводная от неопределенного интеграла равна подынтегральной функции:d∫f(x)dx=f(x)·dx; (∫f(x)dx)'=f(x).
20 Неопределенный интеграл от дифференциала функции равен самой этой функции с точностью до постоянного слагаемого: ∫dF(x)=F(x)+C.
30 Постоянный множитель можно выносить за знак неопределенного интеграла: ∫kf(x)dx=k∫f(x)dx.
40 Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций:
∫[f1(x)+f2(x)-f3(x)]dx=∫f1(x)dx+∫f2(x)dx-∫f3(x)dx
2.2.Таблица интегралов
2.3. Основные методы интегрирования.
1.Непосредственное интегрирование.
Этот способ основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме путем тождественных преобразований.
2. Интегрирование подстановкой (замена переменной).
Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к табличной форме.
В интеграле ∫f(g(x))g’(x)dx заменим t=g(x), dt= g'(x)dx, тогда ∫f(g(x))g’(x)dx=∫f(t)dt.
2. Интегрирование по частям.
При этом способе используют формулу ∫udv=uv-∫vdu (*)
К числу интегралов, вычисляемых по частям, относятся, например, интегралы вида ∫P(x)·f(x)dx, где P(x)- многочлен (в частности, степенная функция), а f(x)- одна из следующих функций: ex, sinax, cosax, lnx, arcsinx, arccosx,arctgx, arcctgx. При этом для интегралов вида ∫P(x)·eaxdx, ∫P(x)sinaxdx, ∫P(x)cosaxdx, вкачестве “u” принимают многочлен P(x), а для интегралов вида ∫P(x)arcsinxdx, ∫P(x)arccosxdx, ∫P(x)arctgxdx, ∫P(x)arcctgxdx, ∫P(x)lnxdxвкачестве “u” принимается lnx, arcsinx, arccosx, arctgx, arcctgx.
Решение типовых задач.
Задача1. Решить методом непосредственного интегрирования
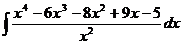
Решение. Сначала преобразуем подынтегральное выражение и получим ∫(x2-6x-8+ 9/x -5x-2)dx.
Воспользуемся свойствами 4 и 3 неопределенного интеграла:
∫(x2-6x-8+ 9/x -5x-2)dx=∫x2dx-6∫xdx-8∫dx+9∫dx/x -5∫x-2dx
Все полученные интегралы табличные, поэтому, применяя формулы интегрирования, получаем:
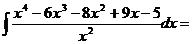


Задача 2. Решить методом непосредственного интегрирования ∫tg2xdx.
Решение. Воспользуемся соотношением tg2x =1/cos2x -1 и преобразуем заданный интеграл:
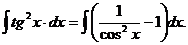

Воспользуемся свойством 4 неопределенного интеграла и формулами интегрирования:
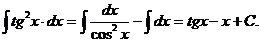
Задача 3. Решить методом подстановки ∫(x3+5)4·x2·dx
Решение. Заменим x3+5=t и продифференцируем это равенство: d(x3+5)=dt; 3x2·dx=dt. Сделаем замены в заданном интеграле: ∫(x3+5)4·x2·dx= 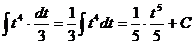
Возвращаясь к первоначальной переменой x, получаем: ∫(x3+5)4·x2dx = (x3+5)5/15 + C
Задача 4. Решить методом подстановки ∫sin7xcosx·dx.
Решение. Заменим в подынтегральном выражении sinx=t и продифференцируем это равенство: cosxdx=dt. Делаем замену в заданном интеграле: ∫sin7xcosxdx = ∫t7·dt = t8/8 + C или ∫sin7xcosxdx =sin8x/8+C.
Решение интеграла способом подстановки оформляют так:
∫sin7x cosx·dx= 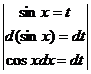 =∫t7·dt=
=∫t7·dt= 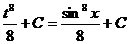 .
.
Задача 5. Решить методом интегрирования по частям ∫xlnxdx.
Решение. Согласно данным выше рекомендациям, заменим lnx=u, а оставшееся выражение xdx=dv. Найдем du=d(lnx)=dx/x и функцию v из равенства dv=xdx. Тогда ∫dv=∫xdx, откуда v=x2/2 (полагаем С=0). Теперь, зная u=lnx, v=x2/2 и du=dx/x, применим формулу интегрирования по частям ∫udv = uv-∫vdu. В нашем примере имеем:
∫lnx·xdx= 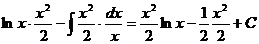 или ∫xlnxdx=
или ∫xlnxdx= 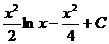 .
.
Примечание: В некоторых случаях для приведения интеграла к табличному виду формулу интегрирования по частям применяют последовательно несколько раз.
Задача 6. Решить методом интегрирования по частям ∫x2·exdx
Решение: Согласно данным выше рекомендациям обозначим x2=u, а оставшееся выражение е2dx=dv. Найдем du=d(x2)=2xdx и функцию v из равенства dv=exdx, тогда ∫dv=∫exdx, откуда v=ex.
Зная u=x2, v=ex и du=2xdx, применив формулу (*), получаем: ∫x2exdx=x·ex-2∫xexdx.
Полученный в правой части интеграл ∫xexdx проще данного, но не табличный. Поэтому решаем его, вновь применяя формулу (*). Обозначим x=u и dv=exdx. Найдем du=dx; v=∫exdx=ex.
Решаем ∫xexdx=x·ex-∫exdx=xex-ex+С. Окончательно получаем: ∫x2exdx=x2·ex-2(xex-ex)+C=ex(x2-2x+2)+С.
При решении интегралов по частям рекомендуется следующая форма записи: ∫x2exdx= 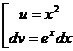
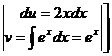 x2·ex-2∫xexdx=x2ex-2(xex-∫exdx)=
x2·ex-2∫xexdx=x2ex-2(xex-∫exdx)= 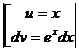
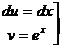 =x2ex-2xex+2ex+C = ex(x2-2x+2)+С.
=x2ex-2xex+2ex+C = ex(x2-2x+2)+С.
2.4. Определенный интеграл
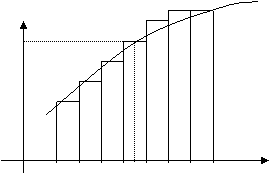
Рассмотрим функцию y=f(x), непрерывную на отрезке [a,b]. Разобьем [a,b] на n элементарных отрезков∆xi произвольной длины, возьмем на каждом отрезке ∆xi произвольную точку ci и вычислим значение функции f(ci) в этих точках (см. Рис.7).
Определение 1. Интегральной суммой для функции y=f(x) на отрезке [a,b] называется сумма произведений длины элементарных отрезков ∆xi на значения функции f(ci) в произвольных точках этих отрезков: 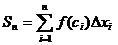 .
.
Определение 2. Определенным интегралом от функции f(x) на отрезке [a,b] называется предел (если он существует) интегральной суммы для функции f(x) на отрезке [a,b], не зависящий от способа разбиения отрезка [a,b] и выбора точек ci, найденный при условии, что длины элементарных отрезков (включая и максимальный ∆xmax) стремятся к нулю.
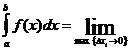
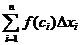
 y
y
f(ci)
Рис.7.
axicixi+1bx
Геометрически определенный интеграл  dx (a<b и f(x)>0) равен a площади криволинейной трапеции SaABb, ограниченной кривой y=f(x), отрезком [a,b] оси Ox и прямыми x=a и x=b (рис. 8).
dx (a<b и f(x)>0) равен a площади криволинейной трапеции SaABb, ограниченной кривой y=f(x), отрезком [a,b] оси Ox и прямыми x=a и x=b (рис. 8).
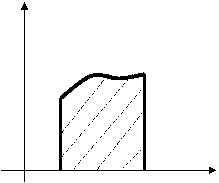
y
y = f (x)
x = a x = b Рис. 8.
y = 0 x
Формула Ньютона-Лейбница. Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.
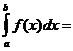 F(x)
F(x) 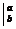 =F(b)-F(a), где
=F(b)-F(a), где 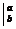 - знак двойной подстановки.
- знак двойной подстановки.
Основные свойства определенного интеграла.
Свойство 10 Величина определенного интеграла не зависит от обозначения переменной интегрирования:
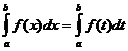
Свойство 20 Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
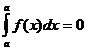
Свойство 30. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный:
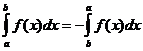
Свойство 40(свойство аддитивности). Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам: если 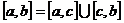 , то
, то
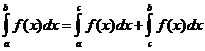
Формула верна и в случае, если точка c лежит вне отрезка [a,b] и функция f(x) непрерывна на отрезках [a,b] и [c,b].
Свойство 50 Постоянный множитель можно выносить за знак определенного интеграла:
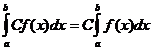
Свойство 60 Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:
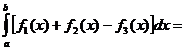

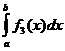
Свойство 70(свойство монотонности). Если подынтегральная функция f(x) на отрезке интегрирования сохраняет постоянный знак, то определенный интеграл представляет собой число того же знака, что и функция, при условии b>a: если f(x)≥0, то и 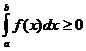
Свойство 80(о среднем значении функции). Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке x=c отрезка интегрирования [a,b] на длину отрезка b-a:
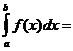 f(c) (b-a), откудаµ=f(c)=
f(c) (b-a), откудаµ=f(c)= 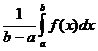 .
.
f(c) называется средним значением функции на отрезке [a,b] (Рис. 9).
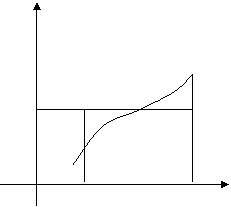 y
y
D
C +

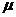 _ E
_ E
B Рис. 9.
AF
aсbx
2.5. Основные методы решения определенных интегралов.
1. Непосредственное интегрирование.
Этот способ основан на использовании свойств определенного интеграла, приведении подынтегрального выражения к табличной форме путем тождественных преобразований и применении формулы Ньютона-Лейбница.
2. Интегрирование подстановкой.
Для решения определенного интеграла 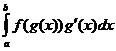 методом подстановки заменяют g(x)=t; dt=g'(x)dx и находят пределы изменения переменной t при изменении x от a до b из соотношений: g(a)=α и g(b)=β.
методом подстановки заменяют g(x)=t; dt=g'(x)dx и находят пределы изменения переменной t при изменении x от a до b из соотношений: g(a)=α и g(b)=β.
Тогда 
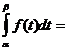
 =
= 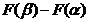 ,
,  где F(t)-первообразная функции f(g(x))=f(t).
где F(t)-первообразная функции f(g(x))=f(t).
3. Интегрирование по частям.
При этом способе используют формулу:  (**)
(**)
Подробные рекомендации по решению интегралов по частям даны в описании этого метода применительно к неопределенным интегралам.
Решение типовых задач
Задача 1. Вычислить 
Решение. Данный интеграл решим непосредственным интегрированием. Сначала преобразуем подынтегральное выражение:
 =
= 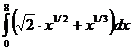 .
.
Применим свойства 6 и 5, в результате чего получим
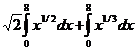
Так как оба интеграла табличные, записываем первообразные функции и применяем формулу Ньютона-Лейбница:
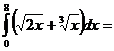

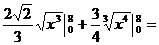
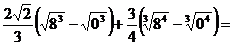
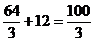
Задача 2. Вычислить 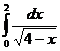
Решение. Решаем интеграл методом подстановки. Введем новую переменную t=4-x и продифференцируем данное равенство: dt=d(4-x); dx=-dt. Найдем новые пределы интегрирования из соотношения t= 4-x: при x1=0 получаем t1=4,
при x2=2 получаем t2=2.
Делаем замену переменной в заданном интеграле:
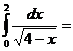
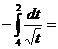
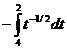
Избавимся от знака минус перед интегралом, воспользовавшись свойством 3:
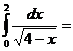
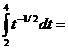
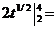

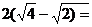
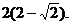
Задача 3. Вычислить 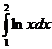
Решение. Будем решать интеграл методом интегрирования по частям. Обозначим lnx=u, dx=dv и найдем du=d(lnx)=dx/x и v=∫dx=x. Применяя к заданному интегралу формулу интегрирования по частям, получим
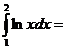
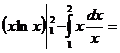
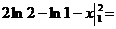
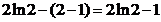 .
.
Контрольное задание № 2
В задачах 41-50 требуется вычислить указанные неопределенные интегралы способом непосредственного интегрирования.
41. 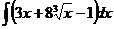 42.
42. 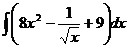
43. 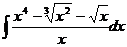 44.
44. 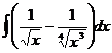
45. 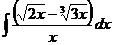 46.
46. 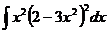
47.  48.
48. 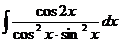
49. 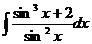 50.
50. 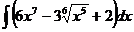
В задачах 51-60 вычислить указанные неопределенные интегралы методом подстановки.
51. 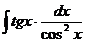 52.
52. 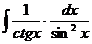
53. 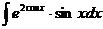 54.
54. 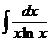
55. 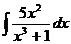 56.
56. 
57.  58.
58. 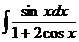
59. 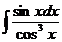 60.
60. 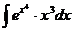
В задачах 61-70 вычислить указанные определенные интегралы.
61. 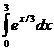 62.
62. 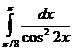
63. 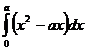 64.
64. 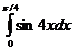
65. 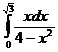 66.
66. 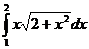
67. 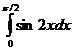 68.
68. 
69. 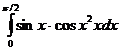 70.
70. 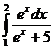
Часть 3. Основы теории вероятностей и математической статистики
3.1. Основные понятия теории вероятностей
Предметом изучения теории вероятностей являются количественные закономерности однородных случайных явлений массового характера.
Определение 1. Событием называется всякий возможный факт, о котором можно сказать, что он произойдет или не произойдет в данных условиях.
Пример. Готовые ампулы, сошедшие с конвейера, могут оказаться либо стандартными, либо нестандартными. Один (любой) исход из указанных двух возможных называются событием.
Различают три вида событий: достоверные, невозможные и случайные.
Определение 2. Достоверным называют то событие, которое при соблюдении некоторых условий не может не произойти, т.е. обязательно произойдет (обозначают Ω).
Пример. Если в урне содержатся только белые шары, то взятый наудачу из урны шар будет обязательно белый. В данных условиях факт появления белого шара будет достоверным событием.
Определение 3. Невозможным называют то событие, которое при соблюдении некоторых условий не может произойти (обозначают Æ).
Пример. Нельзя извлечь белый шар из урны, содержащей только черные шары. В этих условиях факт появления белого шара будет невозможным событием.
Определение 4. Случайным называют событие, которое в одних и тех же условиях может произойти, но может и не произойти (обозначение A, B, A1, A2).
Пример. Монета, брошенная вверх, может упасть так, что на ее верхней стороне окажется либо герб, либо цифра. Здесь появление сверху той или другой стороны монеты является случайным событием.
Определение 5. Испытание - совокупность тех условий или действий, которые могут быть повторены бесконечное число раз.
Пример. Подбрасывание монеты вверх - испытание, а возможный результат, т.е. выпадение на верхней стороне монеты либо герба, либо цифры является событием.
Определение 6. Если события Ai таковы, что при некотором данном испытании может произойти только одно из них и никаких других, не входящих в совокупность, то эти события называются единственно возможными.
Пример. В урне лежат белые и черные шары и никаких других. Взятый наугад один шар может оказаться белым или черным. Эти события являются единственно возможными, т.к. появление шара другой окраски при данном испытании исключено.
Определение 7. Два события A и B называются несовместными, если при данном испытании они не могут произойти вместе.
Пример. Герб и цифра являются единственно возможными и несовместимыми событиями при однократном бросании монеты.
Определение 8. Два события A и B называются совместными (совместимыми) при данном испытании, если появление одного из них не исключает возможность появления другого события при том же испытании.
Пример. Возможно совместное появление орла и цифры при одном бросании двух монет.
Определение 9. События Ai называются равновозможными в данном испытании, если в силу симметрии есть основание считать, что ни одно из этих событий не является более возможным по сравнению с другими.
Пример. Появление любой грани при одном бросании игральной кости является равновозможным событием (при условии, если кость сделана из однородного материала и имеет форму правильного шестигранника).
Определение 10. События называются благоприятствующими (благоприятными) некоторому событию, если появление одного из этих события влечет появление данного события. Случаи, исключающие появление события, называются неблагоприятствующими этому событию.
Пример. В урне имеется 5 белых и 7 черных шаров. При взятии наугад одного шара, в руках может оказаться или белый или черный шар. В данном случае появление белого шара благоприятствует 5 случаев, а появлению черного шара 7 случаев из общего количества 12 возможных случаев.
Определение 11. Два единственно возможных и несовместимых событий называют противоположными друг другу. Если одно из этих событий обозначено A, то противоположное ему событие обозначают символом Ā.
Пример. Попадание в цель и промах; выигрыш и проигрыш по билету лотереи - все это примеры противоположных событий.
Определение 12. Если в результате какой-либо массовой операции, состоящей из n сходных между собой единичных опытов или наблюдений (испытаний), некоторое случайное событие появится m раз, то число m называют частотой случайного события, а отношение m/n называется его частостью.
Пример. Среди первых 20 изделий, сошедших с конвейера, оказалось 3 изделия нестандартных (брак). Здесь число испытаний n=20, частота брака m=3, частость брака m/n = 3/20 = 0,15.
Всякое случайное событие в заданных условиях имеет свою объективную возможность появления, причем у одних событий эта возможность появления больше, у других - меньше. Для количественного сравнения между собой событий по степени возможности их наступления с каждым случайным событием связывают некоторое действительное число, выражающего количественную оценку степени объективной возможности наступления данного события. Это число называют вероятностью события.
Определение 13. Вероятность некоторого события есть числовая мера объективной возможности наступления этого события.
Определение 14. (Классическое определение вероятности). Вероятностью события А называется отношение числа m случаев, благоприятствующих наступлению этого события, к числу n всех возможных случаев, т.е. Р(А) = m/n.
Пример. Урна содержит 5 белых и 7 черных шаров, тщательно перемешанных. Какова вероятность того, что взятый наудачу из урны один шар окажется белым?
Решение. В данном испытании имеется всего 12 возможных случаев, из них 5 благоприятствуют появлению белого шара. Поэтому вероятность появления белого шара Р=5/12.
Определение 15. (Статистическое определение вероятности). Если при достаточно большом числе повторных испытаний по отношению к некоторому событию А будет замечено, что частость события колеблется около некоторого постоянного числа, то событие А имеет вероятность Р(А), приближенно равную частости, т.е. Р(А)~m/n. Частость события при неограниченном числе испытаний называют статистической вероятностью.
Основные свойства вероятности.
10 Если событие А влечет за собой событие В (АÞВ), то вероятность события А не превосходит вероятности события В. Р(А)≤Р(В)
20 Если события А и В равносильны (АÞB, ВÞА, В=А), то их вероятности равны Р(А)=Р(В).
30 Вероятность любого события А не может быть отрицательным числом, т.е. Р(А)≥0
40 Вероятность достоверного события W равна 1. Р(W)=1.
50 Вероятность невозможного события Æ равна 0. Р(Æ)=0.
60 Вероятность любого случайного события А заключена между нулем и единицей 0<Р(А)<1
3.2. Основные формулы комбинаторики
Определение 1. Различные группы по m предметов, составленные из n однородных предметов (m,n), называются соединениями. Предметы, из которых составляют различные соединения, называют элементами.
Существует 3 вида соединений: размещения, перестановки, сочетания.
Определение 2. Размещениями по m элементов из данных n элементов (m≤n) называют такие соединения, которые отличаются друг от друга либо самими элементами, либо их порядком. Например, размещениями из трех предметов a,bиc по два будут следующие соединения: ab, ac, bc, ca, cb, ba. Число размещений из данных n элементов по m обозначают символом Аnm=n(n-1)(n-2)·....·(n-m+1).
Пример. А104=10·9·8·7=5040.
Определение 3. Перестановками из n элементов называют такие соединения, которые отличаются друг от друга только порядком элементов. Рn=Аnn=n(n-1)(n-2)...·3·2·1=n! По определению 0!=1.
Пример. Р5=5!=1·2·3·4·5=120.
Определение 4. Сочетаниями из n элементов по m называются также соединения, которые отличаются друг от друга, по меньшей мере, одним элементом и каждое из которых содержит m различных элементов:
Cnm= 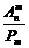 =
=  =
= 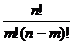
Пример. Найти число сочетаний из 10 элементов по четыре.
Решение.C104= 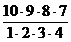 =210.
=210.
Пример. Найти число сочетаний из 20 элементов по 17.
Решение. 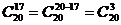 =
= 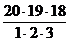 =1040.
=1040.
Числа сочетаний являются коэффициентами в формуле бинома Ньютона (биномиальные коэффициенты):
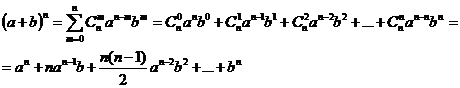
Биномиальные коэффициенты до n=10 можно находить из треугольника Паскаля.
| n \ m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | ||||||||||
| 1 | 1 | 1 | |||||||||
| 2 | 1 | 2 | 1 | ||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
3.3.Теоремы теории вероятностей
3.3.1. Теорема сложения вероятностей
Теорема1.Вероятность наступления одного какого-либо события из двух несовместимых событий А и В равно сумме вероятностей этих событий Р(А+В)=Р(А)+Р(В).
Пример. В урне 5 красных, 7 синих и 8 белых шаров, перемешанных между собой. Какова вероятность того, что взятый наугад один шар окажется не красным?
Решение. Не красный шар - это или белый или синий шары. Вероятность появления белого шара (событие А) равна Р(А)= 8/20 = 2/5. Вероятность появления синего шара (событие В) равна Р(В)= 7/20. Событие, состоящее в появлении не красного шара, означает появление или А или В, т.к. события А и В несовместимы, то применима теорема 1. Искомая вероятность будет равна Р(А+В)=Р(А)+Р(В)=2/5+ +7/20=3/4.
Теорема 2. Вероятность наступления одного из двух событий A или B равно сумме вероятностей этих событий минус вероятность их совместного появления P(A+B)=P(A)+P(B)+P(AB).
3.3.2. Теорема умножения вероятностей
Определение 1. Два события A и B называются независимыми друг от друга, если вероятность одного из них не зависит от наступления или ненаступления другого.
Пример. Пусть A - событие, состоящее в появлении герба при первом бросании монеты, а B - событие, состоящее в появлении герба при втором бросании монеты, то события A и B не зависят друг от друга, т.е. результат первого бросания монеты не может изменить вероятность появления герба при втором бросании монеты.
Определение 2. Два события A и B называются зависящими друг от друга, если вероятность одного из них зависит от наступления или ненаступления другого.
Пример. В урне 8 белых и 7 красных шаров, перемешанных между собой. Событие A - появление белого шара, а событие B - появление красного шара. Будем брать из урны наугад два раза по одному шару, не возвращая их обратно. До начала испытания вероятность появления события A равна P(A)=8/15, и вероятность события B равна P(B)=7/15. Если предположить, что в первый раз был взят белый шар (событие A), то вероятность появления события B при втором испытании будет P(B)=7/14=1/2. Если в первый раз был взят красный шар, то вероятность появления красного шара при втором извлечении равна P(B)=6/14=3/7.
Определение 3. Вероятность события B, вычисленная в предположении, что перед этим наступило связанное с ним событие A, называется условной вероятностью события B и обозначается PA(B).
Теорема 3. Вероятность совместного наступления двух зависимых событий (A и B) равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло,т.е. P(AB)=P(A)·PA(B)=P(B)·PB(A).
Теорема 4. Вероятность совместного наступления нескольких зависимых событий равно произведению вероятности одного из них на условные вероятности всех остальных событий, вычисленные в предположении, что все предыдущие события уже наступили:
P(A1A2A3...Ak)=P(A1)·PA1(A2)·PA1A2·P(A3)...·PA1A2…A k-1 (Ak)
Теорема 5. Вероятность совместного наступления двух независимых событий A и B равна произведению вероятностей этих событий P(AB)=P(A)·P(B).
Теорема 6. Вероятность совместного наступления нескольких независимых событий A1, A2, ... Ak равна произведению их вероятностей, т.е. P(A1A2...Ak)=P(A1)·P(A2)·...·P(Ak).
Пример. Два стрелка делают одновременно по одному выстрелу в одну цель. Какова вероятность того, что оба попадут, если известно, что первый стрелок в среднем дает 7 попаданий, а второй 8 попаданий на каждые 10 выстрелов? Какова вероятность поражения мишени?
Решение. Вероятность попадания первого стрелка (событие A) равна P(A)=0,8, вероятность попадания второго стрелка (событие B) равна P(B)=0,7. События A и B независимы друг от друга, поэтому вероятность совместного наступления этих событий (совместное попадание в цель) найдем по теореме умножения для независимых событий: P(AB)=P(A)P(B)=0,8·0,7=0,56.
Вероятность поражения мишени означает попадание в мишень хотя бы одного стрелка. Так как попадание в мишень первого и второго стрелков являются событиями совместными, то применение теоремы сложения вероятностей для совместных событий дает следующий результат:
P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)·P(B)=0,8+0,7- 0,8·0,7=0,94.
3.3.3.Формула полной вероятности
Определение 4. Если при некотором испытании может произойти одно какое-либо событие из нескольких несовместных A1,A2,...,Ak, и при этом никаких других событий быть не может, но одно из указанных событий обязательно произойдет, то группу событий A1,A2,...,Ak называют полной группой событий.
Теорема 7. Сумма вероятностей событий, образующих полную группу, равна единице: P(A1)+P(A2)+...+P(Ak)=1.
Следствие. Сумма вероятностей двух противоположных событий равна единице: P(A)+P(A)=1.
Если вероятность одного события обозначим через p, вероятность противоположного ему события обозначим через q, тогда p+q=1.
Пример. Вероятность попадания в цель равна 0,94. Найти вероятность непопадания.
Решение. Попадание в цель и непопадание являются противоположными событиями, поэтому, если p=0,94, то q=1-p=1-0,94=0,06.
Теорема 8. Если случайные события A1,A2...An образуют полную систему, и если событие B может осуществляться только совместно с каким-нибудь одним из этих событий, то вероятность наступления события B можно определить по формуле:
P(B)=P(A1)PA1 (B)+P(A2)PA2 (B)+...+P(An)PA n(B)
Это равенство называется формулой полной вероятности.
Пример. На склад готовой продукции поступили изделия из трех цехов, в том числе: 30% из I-го цеха, 45% из II цеха и 25% из III цеха. Среди изделий I цеха брак составляет 0,6%, по II цеху 0,4% и по III цеху-0,16%. Какова вероятность того, что взятое наугад для контроля одно изделие окажется с браком?
Решение. Одно изделие может быть взято или из продукции I цеха (событие A1), или из продукции II цеха (событие A2), или из продукции III цеха (событие A3). Вероятности этих событий будут:
P(A1)=0,30; P(A2)=0,45; P(A3)=0,25.
Вероятность того, что изделие с браком (событие B) будет взято из продукции I цеха, есть условная вероятность PA1(B). Она равна PA1(B)=0,006. Вероятность того, что изделие с браком будет взято из продукции II цеха PA2(B)=0,004 и из продукции III цеха PA3(B)=0,0016.
Теперь по формуле полной вероятности найдем вероятность того, что взятое наугад одно изделие будет с браком:
P(B)=P(A1)PA1(B)+P(A2)PA2(B)+...+P(A3)PA3(B) = 0,3·0,006+0,45·0,004+0,25·0,0016=0,004.
3.3.4. Формула Бернулли
Теорема 9. Пусть производится n независимых повторных испытаний по отношению к некоторому событию A. Пусть вероятность появления этого события в каждом отдельном испытании остается неизменно равной p, а вероятность появления противоположного события Ā, есть q.
Тогда вероятность появления интересующего нас события A равно m раз при указанных n испытаниях рассчитывается по формуле Бернулли:
Pm, n=  pmqn-m , так как
pmqn-m , так как 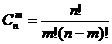 , то Pm,n=
, то Pm,n= 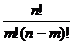 ·pm·qn-m
·pm·qn-m
Пример. Коэффициент использования станка в среднем равен 0,8. В цехе имеется 5 станков. Какова вероятность того, что в некоторый момент времени окажутся работоспособными только 3 станка?
Решение. Задача подходит под схему повторных испытаний и решается по формуле Бернулли: n=5, m=3, p=0,8 и q=1-0,8=0,2: P3,5= 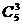 (0,8)3·(0,2)2=0,2084.
(0,8)3·(0,2)2=0,2084.
3.4.Случайные величины и их числовые характеристики
Определение 1. Случайной величиной называется переменная величина, которая в результате опыта принимает одно значение, причем неизвестно заранее, какое именно (обозначается последними буквами латинского алфавита X, Y, Z, X1, X2).
Случайные величины бывают двух видов: дискретные и непрерывные.
Определение 2. Дискретной называется случайная величина, которая может принимать лишь отдельные, изолированные друг от друга значения.
Случайная дискретная величина задается законом распределения, связывающим принимаемые ею значения xi и вероятности их принятия pi. Закон распределения чаще всего задается в табличной форме.
Графическое представление закона распределения случайной дискретной величины называетсямногоугольником распределения.
3.4.1. Числовые характеристики дискретной случайной величины.
1) Математическое ожидание.
Определение 3. Математическое ожидание случайной дискретной величины X с конечным числом значений называется сумма произведений возможных ее значений на их вероятности:
M(X) =μ= x1p1 + x2p2 +...+ xnpn = 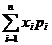 .
.
Вероятности всех значений случайной дискретной величины удовлетворяют условию нормировки:
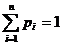
Свойства математического ожидания.
10 Математическое ожидание постоянной (неслучайной) величины С равно самой постоянной M(C)=C.
20 Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий слагаемых M(X1 ± X2 ±...± Xn) = M(X1) ± M(X2) ±…± M(Xn).
30 Константу можно вынести за знак математического ожидания M(CX)=CM(X).
40 Математическое ожидание произведения нескольких независимых случайных величин равно произведению математических ожиданий этих величин: M(X1X2...Xn) = M(X1)M(X2)...M(X)n.
2) Дисперсия дискретной случайной величины.
Определение 4. Дисперсией случайной дискретной величины X называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания.
D(X) = M{[X-M(X)]2} =  , где M(X) = μ
, где M(X) = μ
Для вычисления дисперсии более удобна формула: D(X)=M(X2)-[M(X)]2, т.е. дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания.
Свойства дисперсии.
10 Дисперсия постоянной величины равна нулю D(С) = 0.
20 Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(CX) = C2D(X).
30 Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин: D(X1+...+Xn) = D(X1)+...+D(Xn).
40 Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин D(X-Y)=D(X)+D(Y).
3). Среднее квадратическое отклонение
Определение 5. Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсииσ(X)= 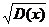 .
.
Пример. Найти математическое ожидание и дисперсию случайной величины X, которая задана следующим законом распределения:
| X | 1 | 2 | 5 |
| p | 0,3 | 0,5 | 0,2 |

 Решение. Найдем математическое ожидание: M(X)=1·0,3+2·0,5+ +5·0,2=2,3. Найдем все возможные значения квадрата отклонения.
Решение. Найдем математическое ожидание: M(X)=1·0,3+2·0,5+ +5·0,2=2,3. Найдем все возможные значения квадрата отклонения.
[x1-M(x)]2=(1-2,3)2=1,69 [x2-M(x)]2=(2-2,3)2=0,09 [x3-M(x)]2=(5-2,3)2=7,29
Напишем закон распределения квадрата отклонения
| [xi-M(x)]2 | 1,69 | 0,09 | 7,29 |
| Pi | 0,3 | 0,5 | 0,2 |
Найдем дисперсию: D(x)=1,69·0,3+0,09·0,5+7,29·0,2=2,01.
3.4.2. Числовые характеристики непрерывной случайной величины.
Определение 6. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Определение 7. Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение меньше x, т.е. F(x)=P(X<x).
Свойства интегральной функции распределения
10 Значения интегральной функции распределения принадлежат отрезку0≤F(x) ≤1.
20 Функция распределения есть неубывающая функция.
Следствие 1. Вероятность того, что случайная величина X попадет в интервал (a,b), равна приращению ее интегральной функции распределения на этом интервале P(a<x<b)=F(b)-F(a).
Следствие 2. Вероятность того, что случайная непрерывная величина X примет одно определенное значение равна нулю P(X=x1)=0.
30 Если возможные значения случайной величины X принадлежат интервалу (a,b), то F(x)=0 при x≤a и F(x)=1 при x≥a.
Определение 8. Дифференциальной функцией распределения f(x) (или плотностью вероятности) называется производная от интегральной функции f(x)=F'(x).
Интегральная функция является первообразной для дифференциальной функции, поэтому вероятность того, что случайная непрерывная величина xпримет значение, принадлежащее интервалу (a,b), определяется равенством: P(a<x<b)= 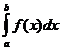 =F(b)-F(a)Зная дифференциальную функцию, можно найти функцию распределения: F(x)=
=F(b)-F(a)Зная дифференциальную функцию, можно найти функцию распределения: F(x)= 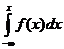
Свойства дифференциальной функции распределения
10 Дифференциальная функция распределения есть функция неотрицательная f(x) ≥0
20 Несобственный интеграл от дифференциальной функции распределения равен единице (условие нормировки):  .
.
1)Математическое ожидание.
Математическим ожиданием случайной непрерывной величины X, возможные значения которой принадлежат отрезку (a,b), называется определенный интеграл:
M(X)= 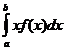 , где f(x)-плотность вероятности случайной величины X.
, где f(x)-плотность вероятности случайной величины X.
2) Дисперсия.
Дисперсия непрерывной случайной величины X есть математическое ожидание квадрата отклонения зтой величины от ее математического жидания D(X) = M{[X - M(X)]2}.Следовательно, если возможные значения случайной величины X принадлежат отрезку (a;b), то
D(x)= 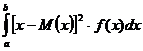 или
или
D(x)= 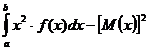
3) Среднее квадратическое отклонение определяется так:σ(x) = 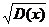
Пример. Найти дисперсию случайной величины X, заданной интегральной функцией
F(x)= 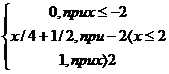

Решение. Найдем дифференциальную функцию:
f(x)=F’(x)= 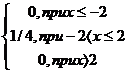

Выислим математическое ожидание M(x) = 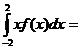
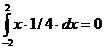 .
.
Найдем искомую дисперсию D(x) = 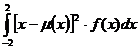 =
= 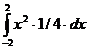 = 2/4
= 2/4 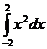 =4/3.
=4/3.
3.4.3.Вероятность попадания нормально распределенной случайной величины X в заданный интервал
Определение 9. Распределение вероятностей случайной непрерывной величины X называется нормальным, если плотность вероятности описывается формулой:
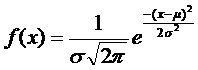 , где μ - математическое ожидание, σ - среднее квадратическое отклонение.
, где μ - математическое ожидание, σ - среднее квадратическое отклонение.
Определение 10. Нормальное распределение с параметрами μ = 0,σ = 1 называется нормированным или стандартным. Плотность вероятности нормированного нормального распределения описывается следующей формулой: 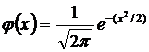 .
.
Значения данной функции для неотрицательных значений затабулированы. В силу четности функции φ(x) значения для отрицательных чисел легко определить φ(-x)= φ(x).
Пример. Математическое ожидание нормального распределенной случайной величины X равно μ=3 и среднее квадратическое отклонение σ =2. Написать дифференциальную функцию X.
Решение. f(x)= 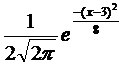
Если случайная величина X распределена по нормальному закону, то вероятность ее попадания в интервал (a,b) определяется следующим образом:
P(a<x<b) = 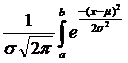 dx=F(b)-F(a).
dx=F(b)-F(a).
Введя новую переменную t=(x-μ)/σ, получим общую формулу для нахождения вероятности попадания нормально распределенной случайной величины в заданный интервал:
P(a<x<b) = P(α<t<β) = 
где 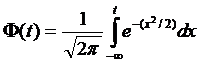 - интегральная функция распределения нормированной нормальной величины.
- интегральная функция распределения нормированной нормальной величины.
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10,50).
Решение.a=10, b=50, σ =10, μ=30
P(10<x<50) = 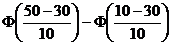 =2Ф(2)
=2Ф(2)
Из таблицы находим Ф(2) = 0,4772 и окончательно имеем P(10<x<50) = 2·0,4772 = 0,9544
4.Элементы математической статистики
4.1. Выборочный метод
Определение 1. Генеральной совокупностью называют множество объектов, однородных относительно некоторого признака, из которого производится выборка.
Определение 2. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Определение 3. Объемом совокупности (генеральной или выборочной) называют число объектов этой совокупности.
Определение 4. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Определение 5. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Определение 6. Выборка называется репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности, и если все объекты имеют одинаковую вероятность попасть в выборку.
Определение 7. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Чаще всего выборки задаются в виде статистического ряда. Различают дискретный и интервальный статистические ряды.
Дискретный статистический ряд задается таблицей, в которой указываются варианты (xi), частоты (mi) и относительные частоты их встречаемости.
| xi | x1 | x2 | x3 | … | xk |
| mi | m1 | m2 | m3 | … | mk |
| Pi* | m1 n | m2 n | m3 n | … | mk n |
Графическое изображение дискретного статистического ряда называетсяполигоном частот (относительных частот).
 |
 Интервальный статистический ряд для случайных непрерывных величин и для случайных дискретных величин при больших объемах выборок. Интервальный ряд представляет собой таблицу, в которой указаны частичные интервалы (∆xi), плотности частот (mi/∆xi) и плотности относительных частот.
Интервальный статистический ряд для случайных непрерывных величин и для случайных дискретных величин при больших объемах выборок. Интервальный ряд представляет собой таблицу, в которой указаны частичные интервалы (∆xi), плотности частот (mi/∆xi) и плотности относительных частот.
Нужно правильно выбрать ширину классового интервала. Число интервалов должно зависеть от размаха выборки и её объёма.
| Частичные интервалы | [x1, x2] | [x2, x3] | … | [xk–1, xk] | ||
| mi | m1 | m2 | … | mk | n = | |
| Pi* | m1 n | m2 n | … | mk n | ||
| Гистограмма частот | mi Dx | m1 Dx1 | m1 Dx2 | … | mk Dxk | Площадь гистограммы равна n |
| Гистограмма относительных частот | Pi* Dx | P1* Dx1 | P2* Dx2 | … | Pk* Dxk | Площадь гистограммы равна 1 |
| Накопленные частоты (кумулята) | å m i | m1 | m1 +m2 | … | n |
Графическое изображение интервального статистического ряда называетсягистограммой.
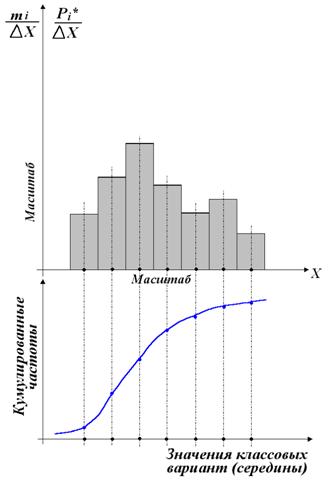 |
Дата добавления: 2018-05-13; просмотров: 252; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!